Difference between revisions of "Purdom's, Boost Graph Library"
| [unchecked revision] | [checked revision] |
| (One intermediate revision by the same user not shown) | |||
| Line 5: | Line 5: | ||
= Links = | = Links = | ||
| − | [http://www.boost.org/libs/graph/doc/ | + | [http://www.boost.org/libs/graph/doc/ Boost Graph Library] (function <code>[http://www.boost.org/libs/graph/doc/transitive_closure.html transitive_closure]</code>). |
| − | |||
= Locality of data and computations = | = Locality of data and computations = | ||
| Line 16: | Line 15: | ||
== Scalability of the algorithm == | == Scalability of the algorithm == | ||
== Scalability of of the algorithm implementation == | == Scalability of of the algorithm implementation == | ||
| + | |||
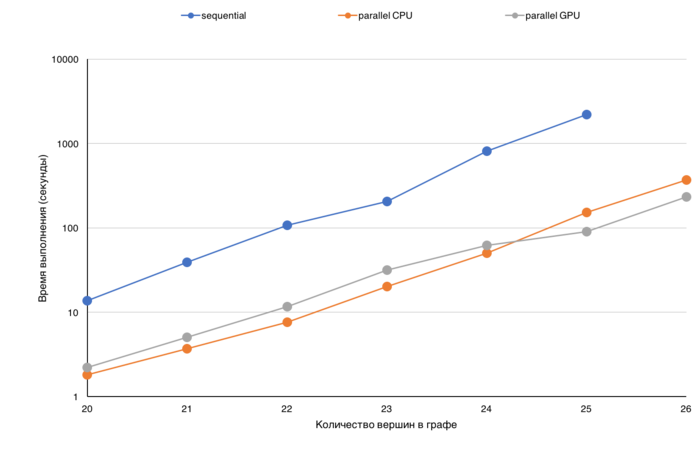
| + | In order to demonstrate efficiency, we present the graphs of the execution times for different modes of computation as functions of the size of the input graph. | ||
| + | |||
| + | The execution time was chosen as the main characteristic for this comparison because the performance (defined as the number of arcs in the graph that are processed by the algorithm in a second) does not reflect the actual situation for this operation. The reason is that the complexity of this implementation of Purdom's algorithm depends on the number of arcs in the graph nonlinearly. Moreover, it also depends on the structure of the graph (e.g., on its number of strongly connected components). | ||
| + | |||
| + | [[file:Замыкание scaling wide.png|thumb|center|700px|Figure 1. Parallel implementation of Purdom's algorithm: scalability of various versions: the execution time as a function of the graph size.]] | ||
| + | |||
| + | By analyzing the execution time, one can assess how the efficiency of processing reduces with the increase in the size of the graph (the data do not fit in the cache, GPU memory, etc.). Each graduation on the axe X in fig. 3 means the doubling in the graph size. The figure helps to assess the corresponding increase in the execution time. It is also possible to compare execution times for different versions, for instance, the versions for a serial CPU, a parallel CPU, or a parallel GPU. The graphs in the figure demonstrate the execution time of these three versions for graph sizes varying from 2^20 to 2^26. The scale on this diagram is logarithmic. | ||
= Dynamic characteristics and efficiency of the algorithm implementation = | = Dynamic characteristics and efficiency of the algorithm implementation = | ||
Latest revision as of 15:06, 6 July 2022
Primary author of this description: I.V.Afanasyev.
Contents
1 Links
Boost Graph Library (function transitive_closure).
2 Locality of data and computations
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
2.1.2 Quantitative estimation of locality
3 Scalability of the algorithm and its implementations
3.1 Scalability of the algorithm
3.2 Scalability of of the algorithm implementation
In order to demonstrate efficiency, we present the graphs of the execution times for different modes of computation as functions of the size of the input graph.
The execution time was chosen as the main characteristic for this comparison because the performance (defined as the number of arcs in the graph that are processed by the algorithm in a second) does not reflect the actual situation for this operation. The reason is that the complexity of this implementation of Purdom's algorithm depends on the number of arcs in the graph nonlinearly. Moreover, it also depends on the structure of the graph (e.g., on its number of strongly connected components).
By analyzing the execution time, one can assess how the efficiency of processing reduces with the increase in the size of the graph (the data do not fit in the cache, GPU memory, etc.). Each graduation on the axe X in fig. 3 means the doubling in the graph size. The figure helps to assess the corresponding increase in the execution time. It is also possible to compare execution times for different versions, for instance, the versions for a serial CPU, a parallel CPU, or a parallel GPU. The graphs in the figure demonstrate the execution time of these three versions for graph sizes varying from 2^20 to 2^26. The scale on this diagram is logarithmic.