Difference between revisions of "Bellman-Ford algorithm"
| (44 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{algorithm | {{algorithm | ||
| − | | name = | + | | name = Bellman-Ford algorithm |
| serial_complexity = <math>O(|V||E|)</math> | | serial_complexity = <math>O(|V||E|)</math> | ||
| pf_height = <math>N/A, max O(|V|) </math> | | pf_height = <math>N/A, max O(|V|) </math> | ||
| Line 41: | Line 41: | ||
2. Relaxation of the set of arcs <math>E</math>: | 2. Relaxation of the set of arcs <math>E</math>: | ||
| − | (a) For each arc <math>e=(v,z) \in E</math>, the new expected distance is calculated: <math>t | + | (a) For each arc <math>e=(v,z) \in E</math>, the new expected distance is calculated: <math>t' (z)=t(v)+ w(e)</math>. |
| − | (b) If <math>t | + | (b) If <math>t' (z)< t(z)</math>, then the assignment <math>t(z) := t' (z)</math> (relaxation of the arc <math>e</math>) is performed. |
3. The algorithm continues to work as long as at least one arc undergoes relaxation. | 3. The algorithm continues to work as long as at least one arc undergoes relaxation. | ||
| Line 92: | Line 92: | ||
The Bellman-Ford algorithm has a considerable parallelization resource. First, the search for shortest paths can be independently performed for all the nodes (parallel vertical planes in figure 1). Second, the search for shortest paths beginning in a fixed node <math>u</math> can also be made in parallel: the initialization of the original paths ([2]) requires <math>|V|</math> parallel operations, and the relaxation of all arcs costs <math>O(|E|)</math> parallel operations. | The Bellman-Ford algorithm has a considerable parallelization resource. First, the search for shortest paths can be independently performed for all the nodes (parallel vertical planes in figure 1). Second, the search for shortest paths beginning in a fixed node <math>u</math> can also be made in parallel: the initialization of the original paths ([2]) requires <math>|V|</math> parallel operations, and the relaxation of all arcs costs <math>O(|E|)</math> parallel operations. | ||
| − | + | Thus, if <math>O(|E|)</math> processors are available, then the algorithm terminates after at most <math>|V|</math> steps. Actually, a smaller number of steps are usually required, namely, <math>O(r)</math> steps. (This number is the maximum length of the shortest paths outgoing from the chosen source node <math>u</math>). | |
| − | + | It follows that the width of the parallel form of the Bellman-Ford algorithm is <math>O(|E|)</math>, while its height is <math>O(r) | r < |V|</math>. | |
| − | [[ | + | The [[algorithm of Δ-stepping]] can be regarded as a parallel version of the Bellman-Ford algorithm. |
=== Input and output data of the algorithm === | === Input and output data of the algorithm === | ||
| − | ''' | + | '''Input data''': weighted graph <math>(V, E, W)</math> (<math>|V|</math> nodes <math>v_i</math> and <math>|E|</math> arcs <math>e_j = (v^{(1)}_{j}, v^{(2)}_{j})</math> with weights <math>f_j</math>), source node <math>u</math>. |
| − | ''' | + | '''Size of input data''': <math>O(|V| + |E|)</math>. |
| − | ''' | + | '''Output data''' (possible variants): |
| − | # | + | |
| − | # | + | # for each node <math>v</math> of the original graph, the last arc <math>e^*_v = (w, v)</math> lying on the shortest path from <math>u</math> to <math>v</math> or the corresponding node <math>w</math>; |
| + | # for each node <math>v</math> of the original graph, the summarized weight <math>f^*(v)</math> of the shortest path from <math>u</math> to <math>v</math>. | ||
| − | ''' | + | '''Size of output data''': <math>O(|V|)</math>. |
=== Properties of the algorithm === | === Properties of the algorithm === | ||
| − | + | The Bellman-Ford algorithm is able to identify cycles of negative length in a graph. An arc <math>e = (v, w)</math> lies on such a cycle if the shortest distances <math>d(v) </math> calculated by the algorithm satisfy the condition | |
:<math> | :<math> | ||
d(v) + f(e) < d(w), | d(v) + f(e) < d(w), | ||
</math> | </math> | ||
| − | + | where <math>f(e)</math> is the weight of the arc <math>e</math>. This condition can be verified for all the arcs of the graph in time <math>O(|E|)</math>. | |
== Software implementation of the algorithm == | == Software implementation of the algorithm == | ||
=== Implementation peculiarities of the serial algorithm === | === Implementation peculiarities of the serial algorithm === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Possible methods and considerations for parallel implementation of the algorithm === | === Possible methods and considerations for parallel implementation of the algorithm === | ||
| − | + | A program implementing the algorithm for finding shortest paths consists of two parts. One part is responsible for the general coordination of computations, as well as parallel computations on a multi-core CPU. The other, GPU part is only responsible for computations on a graphic accelerator. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | === Run results === | ||
=== Conclusions for different classes of computer architecture === | === Conclusions for different classes of computer architecture === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== References == | == References == | ||
Latest revision as of 16:33, 4 July 2022
| Bellman-Ford algorithm | |
| Sequential algorithm | |
| Serial complexity | [math]O(|V||E|)[/math] |
| Input data | [math]O(|V| + |E|)[/math] |
| Output data | [math]O(|V|^2)[/math] |
| Parallel algorithm | |
| Parallel form height | [math]N/A, max O(|V|) [/math] |
| Parallel form width | [math]O(|E|)[/math] |
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
The Bellman-Ford algorithm[1][2][3] was designed for finding the shortest paths between nodes in a graph. For a given weighted digraph, the algorithm finds the shortest paths between a singled-out source node and the other nodes of the graph. The Bellman-Ford algorithm scales worse than other algorithms for solving this problem (the complexity is [math]O(|V||E|)[/math] against [math]O(|E| + |V|\ln(|V|))[/math] for Dijkstra's algorithm). However, its distinguishing feature is the applicability to graphs with arbitrary (including negative) weights.
1.2 Mathematical description of the algorithm
Let [math]G = (V, E)[/math] be a given graph with arc weights [math]f(e)[/math] f(e) and the single-out source node [math]u[/math]. Denote by [math]d(v)[/math] the shortest distance between the source node [math]u[/math] and the node [math]v[/math].
The Bellman-Ford algorithm finds the value [math]d(v)[/math] as the unique solution to the equation
- [math] d(v) = \min \{ d(w) + f(e) \mid e = (w, v) \in E \}, \quad \forall v \ne u, [/math]
with the initial condition [math]d(u) = 0[/math].
1.3 Computational kernel of the algorithm
The algorithm is based on the principle of arc relaxation: if [math]e = (w, v) \in E[/math] and [math]d(v) \gt d(w) + f(e)[/math], then the assignment [math]d(v) \leftarrow d(w) + f(e)[/math] is performed.
1.4 Macro structure of the algorithm
The algorithm successively refines the values of the function [math]d(v)[/math].
- At the very start, the assignment [math]d(u) = 0[/math], [math]d(v) = \infty[/math], [math]\forall v \ne u[/math] is performed.
- Then [math]|V|-1[/math] iteration steps are executed. At each step, all the arcs of the graph undergo the relaxation.
The structure of the algorithm can be described as follows:
1. Initialization: all the nodes are assigned the expected distance [math]t(v)=\infty[/math]. The only exception is the source node for which [math]t(u)=0[/math] .
2. Relaxation of the set of arcs [math]E[/math]:
(a) For each arc [math]e=(v,z) \in E[/math], the new expected distance is calculated: [math]t' (z)=t(v)+ w(e)[/math].
(b) If [math]t' (z)\lt t(z)[/math], then the assignment [math]t(z) := t' (z)[/math] (relaxation of the arc [math]e[/math]) is performed.
3. The algorithm continues to work as long as at least one arc undergoes relaxation.
Suppose that the relaxation of some arcs was still performed at the [math]|V|[/math]-th iteration step. Then the graph contains a cycle of negative length. An arc [math]e=(v,z)[/math] lying on such cycle can be found by testing the condition [math]t(v)+w(e)\lt d(z)[/math] (this condition can be verified for all the arcs in linear time).
1.5 Implementation scheme of the serial algorithm
The serial algorithm is implemented by the following pseudo-code:
Input data:
graph with nodes V and arcs E with weights f(e);
source node u.
Output data: distances d(v) from the source node u to each node v ∈ V.
for each v ∈ V do d(v) := ∞
d(u) = 0
for i from 1 to |V| - 1:
for each e = (w, v) ∈ E:
if d(v) > d(w) + f(e):
d(v) := d(w) + f(e)
1.6 Serial complexity of the algorithm
The algorithm performs [math]|V|-1[/math] iteration steps; at each step, [math]|E|[/math] arcs are relaxed. Thus, the total work is [math]O(|V||E|)[/math] operations.
The constant in the complexity estimate can be reduced by using the following two conventional techniques:
- Algorithm terminates if no successful relaxation occurred at the current iteration step.
- At the current step, not all the arcs are inspected but only the arcs outgoing from nodes that were involved in successful relaxations at the preceding step. (At the first step, only the arcs outgoing from the source node are examined.)
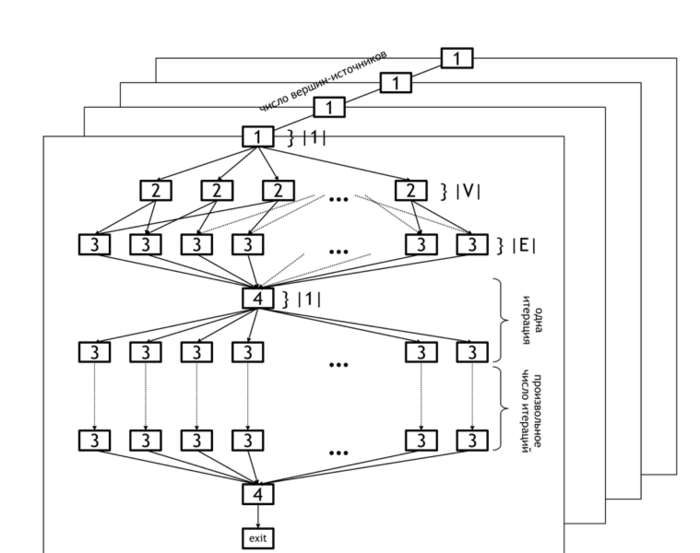
1.7 Information graph
The information graph of the Bellman-Ford algorithm is shown in figure 1. It demonstrates the levels of parallelism in this algorithm.
The lower level of parallelism refers to operations executed within each horizontal plane. The set of all planes represents the upper level of parallelism (because operations in different planes can be carried out concurrently).
The lower level of parallelism in the algorithm graph corresponds to levels [2] and [3], which represent the operations of initialization of the distance array ([2]) and updating of this array based on the data in arcs array ([3]). Operation [4] refers to the test whether any changes occurred at the current iteration and the loop termination if no changes were done.
As already said, the upper level of parallelism consists in the parallel calculation of distances for different source nodes. In the figure, it is illustrated by the set of distinct planes.
1.8 Parallelization resource of the algorithm
The Bellman-Ford algorithm has a considerable parallelization resource. First, the search for shortest paths can be independently performed for all the nodes (parallel vertical planes in figure 1). Second, the search for shortest paths beginning in a fixed node [math]u[/math] can also be made in parallel: the initialization of the original paths ([2]) requires [math]|V|[/math] parallel operations, and the relaxation of all arcs costs [math]O(|E|)[/math] parallel operations.
Thus, if [math]O(|E|)[/math] processors are available, then the algorithm terminates after at most [math]|V|[/math] steps. Actually, a smaller number of steps are usually required, namely, [math]O(r)[/math] steps. (This number is the maximum length of the shortest paths outgoing from the chosen source node [math]u[/math]).
It follows that the width of the parallel form of the Bellman-Ford algorithm is [math]O(|E|)[/math], while its height is [math]O(r) | r \lt |V|[/math].
The algorithm of Δ-stepping can be regarded as a parallel version of the Bellman-Ford algorithm.
1.9 Input and output data of the algorithm
Input data: weighted graph [math](V, E, W)[/math] ([math]|V|[/math] nodes [math]v_i[/math] and [math]|E|[/math] arcs [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math] with weights [math]f_j[/math]), source node [math]u[/math].
Size of input data: [math]O(|V| + |E|)[/math].
Output data (possible variants):
- for each node [math]v[/math] of the original graph, the last arc [math]e^*_v = (w, v)[/math] lying on the shortest path from [math]u[/math] to [math]v[/math] or the corresponding node [math]w[/math];
- for each node [math]v[/math] of the original graph, the summarized weight [math]f^*(v)[/math] of the shortest path from [math]u[/math] to [math]v[/math].
Size of output data: [math]O(|V|)[/math].
1.10 Properties of the algorithm
The Bellman-Ford algorithm is able to identify cycles of negative length in a graph. An arc [math]e = (v, w)[/math] lies on such a cycle if the shortest distances [math]d(v) [/math] calculated by the algorithm satisfy the condition
- [math] d(v) + f(e) \lt d(w), [/math]
where [math]f(e)[/math] is the weight of the arc [math]e[/math]. This condition can be verified for all the arcs of the graph in time [math]O(|E|)[/math].
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
2.2 Possible methods and considerations for parallel implementation of the algorithm
A program implementing the algorithm for finding shortest paths consists of two parts. One part is responsible for the general coordination of computations, as well as parallel computations on a multi-core CPU. The other, GPU part is only responsible for computations on a graphic accelerator.