Difference between revisions of "Boruvka's algorithm"
| [unchecked revision] | [checked revision] |
| (45 intermediate revisions by 2 users not shown) | |||
| Line 54: | Line 54: | ||
Every algorithm for solving this problem must be able to decide which of the already constructed fragments contains a given vertex of the graph. To this end, the data structure called a «system of disjoint sets» (Union-Find) is used. This structure supports the following two operations: | Every algorithm for solving this problem must be able to decide which of the already constructed fragments contains a given vertex of the graph. To this end, the data structure called a «system of disjoint sets» (Union-Find) is used. This structure supports the following two operations: | ||
| − | 1. <math>FIND(v) = w</math> – | + | 1. <math>FIND(v) = w</math> – for a given vertex v, returns the vertex w, which is the root of the fragment that contains v. It is guaranteed that u and v belong to the same fragment if and only if <math>FIND(u) = FIND(v)</math>. |
| − | 2. <math>MERGE(u, v)</math> – | + | 2. <math>MERGE(u, v)</math> – combines two fragments that contain the vertices <math>u</math> and <math>v.</math> (If these vertices already belong to the same fragment, then nothing happens.) It is convenient that, in a practical implementation, this operation would return the value "true" if the fragments were combined and the value "false," otherwise. |
==== Последовательная версия==== | ==== Последовательная версия==== | ||
| − | + | The classical serial algorithm Union-Find is described in a Tarjan's paper. Each vertex v is assigned the indicator to the parent vertex <math>parent(v)</math>. | |
| − | 1. | + | 1. At first, <math>parent(v) := v</math> for all the vertices. |
| − | 2. <math>FIND(v)</math> | + | 2. <math>FIND(v)</math> is executed as follows: set <math>u := v</math>; then follow the indicators <math>u := parent(u)</math> until the relation <math>u = parent(u)</math> is obtained. This is the result of the operation. An additional option is the merging of tree: for all the visited vertices, set <math>parent(u_i) := u</math> or perform the merging operation along the way: <math>parent(u) := parent(parent(u)))</math>. |
| − | 3. <math>MERGE(u, v)</math> | + | 3. <math>MERGE(u, v)</math> is executed as follows: first, find the root vertices <math>u := FIND(u), v := FIND(v)</math>. If <math>u = v</math>, then the original vertices belong to the same fragment and no merging occurs. Otherwise, set either <math>parent(u) := v</math> or <math>parent(v) := u</math>. In addition, one can keep track of the number of vertices in each fragment in order to add the smaller fragment to the greater one rather than otherwise. (Complexity estimates are derived exactly for such an implementation; however, in practice, the algorithm performs well even without counting the number of vertices.) |
=== Implementation scheme of the serial algorithm === | === Implementation scheme of the serial algorithm === | ||
| − | + | In Borůvka's algorithm, the fragments of the minimum spanning tree are build up gradually by joining minimum edges outgoing from each fragment. | |
| − | 1. | + | 1. At the start of the algorithm, each vertex is a separate fragment. |
| − | 2. | + | 2. At each step: |
| − | * | + | * For each fragment, the outgoing edge with the minimum weight is determined. |
| − | * | + | * Minimum edges are added to the minimum spanning tree, and the corresponding fragments are combined. |
| − | 3. | + | 3. The algorithm terminates when only one fragment is left or no fragment has outgoing edges. |
| − | + | The search for minimum outgoing edges can be performed independently for each fragment. Therefore, this stage of computations can be efficiently parallelized (including the use of the mass parallelism of graphic accelerators). | |
| − | + | The merging of fragments can also be implemented in parallel by using the parallel version of the algorithm Union-Find, which was described above. | |
| − | + | An accurate count of the number of active fragments permits to terminate Borůvka's algorithm at one step earlier compared to the above description: | |
| − | 1. | + | 1. At the start of the algorithm, the counter of active fragments is set to zero. |
| − | 2. | + | 2. At the stage of search for minimum edges, the counter is increased by one for each fragment that has outgoing edges. |
| − | 3. | + | 3. At the stage of combining fragments, the counter is decreased by one each time when the operation <math>MERGE(u, v)</math> returns the value "true". |
| − | + | If, at the end of an iteration, the value of the counter is 0 or 1, then the algorithm stops. Parallel processing is possible at the stage of sorting edges by weight; however, the basic part of the algorithm is serial. | |
| − | |||
=== Serial complexity of the algorithm === | === Serial complexity of the algorithm === | ||
| − | + | The serial complexity of Borůvka's algorithm for a graph with <math>|V|</math> vertices and <math>|E|</math> edges is <math>O(|E| \ln(|V|))</math> operations. | |
=== Information graph === | === Information graph === | ||
| − | + | There are two levels of parallelism in the above description: the parallelism in the classical Borůvka's algorithm (lower level) and the parallelism in the processing of a graph that does not fit in the memory. | |
| − | ''' | + | '''Lower level of parallelism''': search for minimum outgoing edges can be performed independently for each fragment, which permits to efficiently parallelize (both on GPU and CPU) this stage of the process. The merging of fragments can also be executed in parallel with the use of the above algorithm Union-Find. |
| − | ''' | + | '''Upper level of parallelism''': constructions of separate minimum spanning trees for each edge list can be performed in parallel. For instance, the overall list of edges can be partitioned into two parts of which one is processed on GPU, while the other is in parallel processed on CPU. |
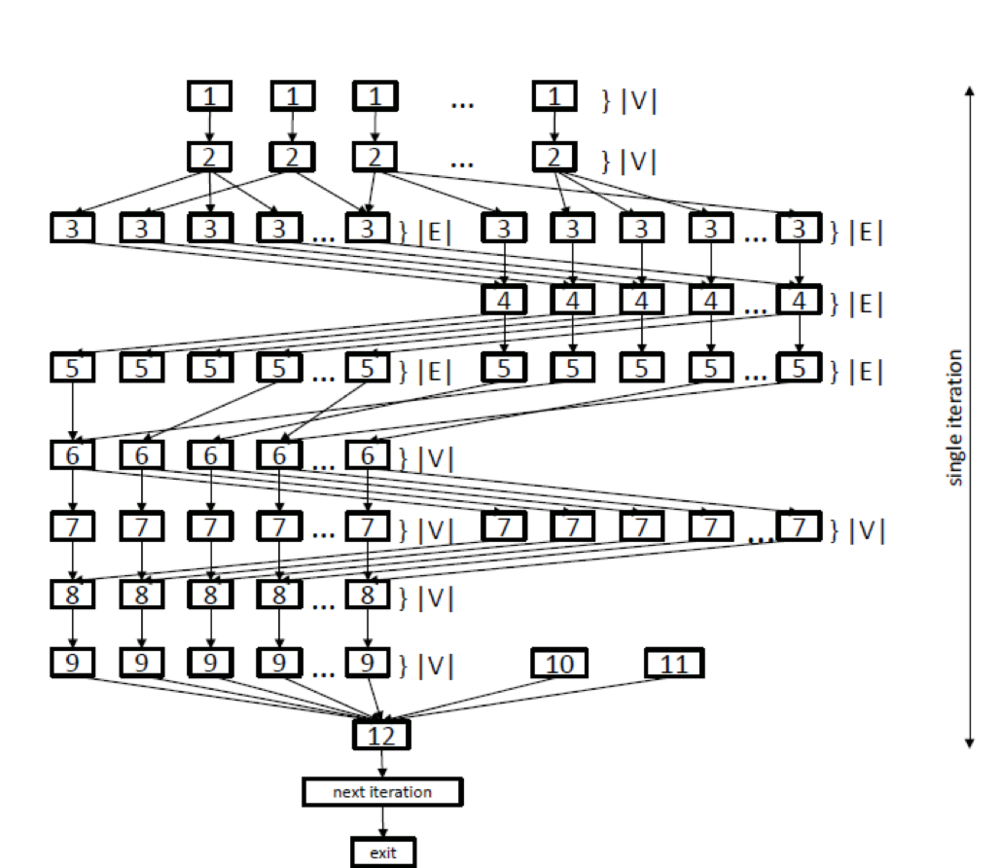
| − | [[file:MST low.png|thumb|center|1000px| | + | [[file:MST low.png|thumb|center|1000px|Figure 1. Information graph of the lower level of parallelism]] |
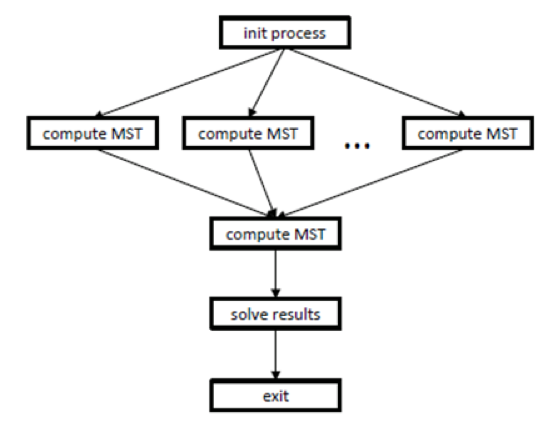
| − | + | Consider the information graphs and their detailed descriptions. One can think that figure 1 shows the information graph of the classical Borůvka's algorithm, while figure 2 shows the information graph of the processing algorithm. | |
| − | + | In the graph shown in figure 1, the lower level of parallelism is represented by levels {3, 4, 5}, which correspond to parallel search operations for minimum outgoing edges, and by levels {6, 7, 8}, which correspond to parallel operations of merging trees. Various copying operations {1, 2, 8, 9} are also performed in parallel. After the body of the loop has been executed, test {12} verifies how many trees are left at the current step. If this number was not changed, the loop terminates; otherwise, the algorithm passes to the next iteration. | |
| − | + | As already said, the upper level of parallelism, illustrated by figure 2, refers to the parallel computation of minimum spanning trees (operation "compute mst") for different parts of the original graph. Prior to this computation, the initialization process ("init process") is performed, and its data are used by the subsequent parallel operations "compute mst". After these parallel computations, the ultimate spanning tree is calculated, and the result obtained is saved to memory ("save results"). | |
| − | [[file:MST up.png|thumb|center|1000px| | + | [[file:MST up.png|thumb|center|1000px|Figure 2. Information graph of the upper level of parallelism]] |
=== Parallelization resource of the algorithm === | === Parallelization resource of the algorithm === | ||
| − | + | Thus, Borůvka's algorithm has two levels of parallelism. | |
| − | + | At the upper level, the minimum spanning trees may be searched for separate parts of the list of graph edges (parallel operations "compute_MST" in figure 2). However, then the final union должно последовать финальное объединение полученных ребер и вычисление минимального остовного дерева для полученного графа, которое будет производиться последовательно. | |
| − | + | Besides, the computation of each minimum spanning tree (parallel operations "compute_MST" in figure 2) has an intrinsic resource of parallelism discussed below. The operations of initialization and copying data (see [1], [2], and [9] in figure 1) can be performed in parallel in <math>O(|V|)</math> steps. The operations of searching for minimum outgoing edges (see [3],[4], and [5]) can also be executed in parallel. при том для каждой дуги и обратной к ней независимо, что даёт <math>2*O(|E|)</math> параллельных операций. Помимо этого, операции объединения деревьев [6], [7], [8] могут так же производиться параллельно за <math>O(|V|)</math> операций. | |
| − | + | As a result, the width of the parallel form of the classical Borůvka's algorithm is | |
| + | <math>O(|E|)</math>. The height of the parallel form depends on the number of steps in the algorithm and is bounded above by <math>O(ln(|V|))</math>. | ||
=== Input and output data of the algorithm === | === Input and output data of the algorithm === | ||
| − | ''' | + | '''Input data''': weighted graph <math>(V, E, W)</math> (<math>|V|</math> vertices <math>v_i</math> and <math>|E|</math> edges <math>e_j = (v^{(1)}_{j}, |
| − | v^{(2)}_{j})</math> | + | v^{(2)}_{j})</math> with weights <math>f_j</math>). |
| − | ''' | + | '''Size of the input data''': <math>O(|V| + |E|)</math>. |
| − | ''' | + | '''Output data''': the list of edges of the minimum spanning tree (for a disconnected graph, the list of minimum spanning trees for all connected components). |
| − | ''' | + | '''Size of the output data''': <math>O(|V|)</math>. |
=== Properties of the algorithm === | === Properties of the algorithm === | ||
| − | # | + | # The algorithm terminates in a finite number of steps because, at each step, the number of fragments reduces by at least one. |
| − | # | + | # Moreover, the number of fragments at least halves at each step; consequently, the total number of steps is at most <math>\log_2 n</math>. This implies an estimate for the complexity of the algorithm. |
== Software implementation of the algorithm == | == Software implementation of the algorithm == | ||
=== Implementation peculiarities of the serial algorithm === | === Implementation peculiarities of the serial algorithm === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Possible methods and considerations for parallel implementation of the algorithm === | === Possible methods and considerations for parallel implementation of the algorithm === | ||
| − | + | A program implementing Borůvka's algorithm consists of two parts: | |
| − | 1. | + | 1. the part that is responsible for the general coordination of computations; |
| − | 2. | + | 2. the part that is responsible for the parallel computations on a multi-core CPU or GPU. |
| − | + | The serial algorithm described above cannot be used in a parallel program: in an implementation of <math>MERGE</math>, the results of operations <math>FIND(u)</math> and <math>FIND(v)</math> may permanently vary, which results in a race condition. A parallel variant of the algorithm is described in paper | |
| − | 1. | + | 1. Each vertex v is assigned the record <math>A[v] = { parent, rank }</math>. At first, <math>A[v] := { v, 0 }</math>. |
| − | 2. | + | 2. The auxiliary operation <math>UPDATE(v, rank_v, u, rank_u)</math>: |
old := A[v] | old := A[v] | ||
| Line 215: | Line 171: | ||
return CAS(A[v], old, new) | return CAS(A[v], old, new) | ||
| − | 3. | + | 3. The operation <math>FIND(v)</math>: |
while v != A[v].parent do | while v != A[v].parent do | ||
| Line 223: | Line 179: | ||
return v | return v | ||
| − | 4. | + | 4. The operation UNION(u, v): |
while true do | while true do | ||
| Line 236: | Line 192: | ||
return true | return true | ||
| − | + | This variant of the algorithm is guaranteed to have the "wait-free" property. In practice, one may use a simplified version with no count of ranks. It has a weaker "lock-free" property but, in a number of cases, wins in speed. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | === Run results === | ||
=== Conclusions for different classes of computer architecture === | === Conclusions for different classes of computer architecture === | ||
| − | |||
| − | |||
| − | |||
== References == | == References == | ||
Latest revision as of 13:54, 5 July 2022
| Алгоритм Борувки | |
| Sequential algorithm | |
| Serial complexity | [math]O(|E|ln(|V|))[/math] |
| Input data | [math]O(|V| + |E|)[/math] |
| Output data | [math]O(|V|)[/math] |
| Parallel algorithm | |
| Parallel form height | [math]max O(ln(|V|)) [/math] |
| Parallel form width | [math]O(|E|)[/math] |
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
The Borůvka algorithm[1][2] was designed for constructing the minimum spanning tree in a weighted undirected graph. It is well parallelizable and is a foundation of the distributed GHS algorithm.
1.2 Mathematical description of the algorithm
Let [math]G = (V, E)[/math] be a connected undirected graph with the edge weights [math]f(e)[/math]. It is assumed that all the edges have distinct weights (otherwise, the edges can be sorted first by weight and then by index).
The Borůvka's algorithm is based on the following two facts:
- Minimum edge of a fragment. Let [math]F[/math] be a fragment of the minimum spanning tree, and let [math]e_F[/math] be an edge with the least weight outgoing from [math]F[/math] (that is, exactly one of its ends is a vertex in [math]F[/math]). If such an edge [math]e_F[/math] is unique, then it belongs to the minimum spanning tree.
- Merging fragments. Let [math]F[/math] be a fragment of the minimum spanning tree of [math]G[/math], while the graph [math]G'[/math] is obtained from [math]G[/math] by merging the vertices that belong to [math]F[/math]. Then the union of [math]F[/math] and the minimum spanning tree of [math]G'[/math] yields the minimum spanning tree of the original graph [math]G[/math].
At the start of the algorithm, each vertex of [math]G[/math] is a separate fragment. At the current step, the outgoing edge with the least weight (if such an edge exists) is chosen for each fragment. The chosen edges are added to the minimum spanning tree, and the corresponding fragments are merged.
1.3 Computational kernel of the algorithm
The basic operations of the algorithm are:
- Search for the outgoing edge with the least weight in each fragment.
- Merging fragments.
1.4 Macro structure of the algorithm
For a given connected undirected graph, the problem is to find the tree that connects all the vertices and has the minimum total weight.
The classical example (taken from Borůvka's paper) is to design the cheapest electrical network if the price for each piece of electric line is known.
Let [math]G=(V,E)[/math] be a connected graph with the vertices [math]V = ( v_{1}, v_{2}, ..., v_{n} )[/math] and the edges [math]E = ( e_{1}, e_{2}, ..., e_{m} )[/math]. Each edge [math]e \in E[/math] is assigned the weight [math]w(e)[/math].
It is required to construct the tree [math]T^* \subseteq E[/math] that connects all the vertices and has the least possible weight among all such trees:
[math] w(T^* )= \min_T( w(T)) [/math].
The weight of a set of edges is the sum of their weights:
[math]w(T)=\sum_{e \in T} (w(T))[/math]
If [math]G[/math] is not connected, then there is no tree connecting all of its vertices.
In this case, it is required to find the minimum spanning tree for each connected component of [math]G[/math]. The collection of such trees is called the minimum spanning forest (abbreviated as MSF).
1.4.1 Auxiliary algorithm: system of disjoint sets (Union-Find)
Every algorithm for solving this problem must be able to decide which of the already constructed fragments contains a given vertex of the graph. To this end, the data structure called a «system of disjoint sets» (Union-Find) is used. This structure supports the following two operations:
1. [math]FIND(v) = w[/math] – for a given vertex v, returns the vertex w, which is the root of the fragment that contains v. It is guaranteed that u and v belong to the same fragment if and only if [math]FIND(u) = FIND(v)[/math].
2. [math]MERGE(u, v)[/math] – combines two fragments that contain the vertices [math]u[/math] and [math]v.[/math] (If these vertices already belong to the same fragment, then nothing happens.) It is convenient that, in a practical implementation, this operation would return the value "true" if the fragments were combined and the value "false," otherwise.
1.4.2 Последовательная версия
The classical serial algorithm Union-Find is described in a Tarjan's paper. Each vertex v is assigned the indicator to the parent vertex [math]parent(v)[/math].
1. At first, [math]parent(v) := v[/math] for all the vertices.
2. [math]FIND(v)[/math] is executed as follows: set [math]u := v[/math]; then follow the indicators [math]u := parent(u)[/math] until the relation [math]u = parent(u)[/math] is obtained. This is the result of the operation. An additional option is the merging of tree: for all the visited vertices, set [math]parent(u_i) := u[/math] or perform the merging operation along the way: [math]parent(u) := parent(parent(u)))[/math].
3. [math]MERGE(u, v)[/math] is executed as follows: first, find the root vertices [math]u := FIND(u), v := FIND(v)[/math]. If [math]u = v[/math], then the original vertices belong to the same fragment and no merging occurs. Otherwise, set either [math]parent(u) := v[/math] or [math]parent(v) := u[/math]. In addition, one can keep track of the number of vertices in each fragment in order to add the smaller fragment to the greater one rather than otherwise. (Complexity estimates are derived exactly for such an implementation; however, in practice, the algorithm performs well even without counting the number of vertices.)
1.5 Implementation scheme of the serial algorithm
In Borůvka's algorithm, the fragments of the minimum spanning tree are build up gradually by joining minimum edges outgoing from each fragment.
1. At the start of the algorithm, each vertex is a separate fragment.
2. At each step:
- For each fragment, the outgoing edge with the minimum weight is determined.
- Minimum edges are added to the minimum spanning tree, and the corresponding fragments are combined.
3. The algorithm terminates when only one fragment is left or no fragment has outgoing edges.
The search for minimum outgoing edges can be performed independently for each fragment. Therefore, this stage of computations can be efficiently parallelized (including the use of the mass parallelism of graphic accelerators).
The merging of fragments can also be implemented in parallel by using the parallel version of the algorithm Union-Find, which was described above.
An accurate count of the number of active fragments permits to terminate Borůvka's algorithm at one step earlier compared to the above description:
1. At the start of the algorithm, the counter of active fragments is set to zero.
2. At the stage of search for minimum edges, the counter is increased by one for each fragment that has outgoing edges.
3. At the stage of combining fragments, the counter is decreased by one each time when the operation [math]MERGE(u, v)[/math] returns the value "true".
If, at the end of an iteration, the value of the counter is 0 or 1, then the algorithm stops. Parallel processing is possible at the stage of sorting edges by weight; however, the basic part of the algorithm is serial.
1.6 Serial complexity of the algorithm
The serial complexity of Borůvka's algorithm for a graph with [math]|V|[/math] vertices and [math]|E|[/math] edges is [math]O(|E| \ln(|V|))[/math] operations.
1.7 Information graph
There are two levels of parallelism in the above description: the parallelism in the classical Borůvka's algorithm (lower level) and the parallelism in the processing of a graph that does not fit in the memory.
Lower level of parallelism: search for minimum outgoing edges can be performed independently for each fragment, which permits to efficiently parallelize (both on GPU and CPU) this stage of the process. The merging of fragments can also be executed in parallel with the use of the above algorithm Union-Find.
Upper level of parallelism: constructions of separate minimum spanning trees for each edge list can be performed in parallel. For instance, the overall list of edges can be partitioned into two parts of which one is processed on GPU, while the other is in parallel processed on CPU.
Consider the information graphs and their detailed descriptions. One can think that figure 1 shows the information graph of the classical Borůvka's algorithm, while figure 2 shows the information graph of the processing algorithm.
In the graph shown in figure 1, the lower level of parallelism is represented by levels {3, 4, 5}, which correspond to parallel search operations for minimum outgoing edges, and by levels {6, 7, 8}, which correspond to parallel operations of merging trees. Various copying operations {1, 2, 8, 9} are also performed in parallel. After the body of the loop has been executed, test {12} verifies how many trees are left at the current step. If this number was not changed, the loop terminates; otherwise, the algorithm passes to the next iteration.
As already said, the upper level of parallelism, illustrated by figure 2, refers to the parallel computation of minimum spanning trees (operation "compute mst") for different parts of the original graph. Prior to this computation, the initialization process ("init process") is performed, and its data are used by the subsequent parallel operations "compute mst". After these parallel computations, the ultimate spanning tree is calculated, and the result obtained is saved to memory ("save results").
1.8 Parallelization resource of the algorithm
Thus, Borůvka's algorithm has two levels of parallelism.
At the upper level, the minimum spanning trees may be searched for separate parts of the list of graph edges (parallel operations "compute_MST" in figure 2). However, then the final union должно последовать финальное объединение полученных ребер и вычисление минимального остовного дерева для полученного графа, которое будет производиться последовательно.
Besides, the computation of each minimum spanning tree (parallel operations "compute_MST" in figure 2) has an intrinsic resource of parallelism discussed below. The operations of initialization and copying data (see [1], [2], and [9] in figure 1) can be performed in parallel in [math]O(|V|)[/math] steps. The operations of searching for minimum outgoing edges (see [3],[4], and [5]) can also be executed in parallel. при том для каждой дуги и обратной к ней независимо, что даёт [math]2*O(|E|)[/math] параллельных операций. Помимо этого, операции объединения деревьев [6], [7], [8] могут так же производиться параллельно за [math]O(|V|)[/math] операций.
As a result, the width of the parallel form of the classical Borůvka's algorithm is [math]O(|E|)[/math]. The height of the parallel form depends on the number of steps in the algorithm and is bounded above by [math]O(ln(|V|))[/math].
1.9 Input and output data of the algorithm
Input data: weighted graph [math](V, E, W)[/math] ([math]|V|[/math] vertices [math]v_i[/math] and [math]|E|[/math] edges [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math] with weights [math]f_j[/math]).
Size of the input data: [math]O(|V| + |E|)[/math].
Output data: the list of edges of the minimum spanning tree (for a disconnected graph, the list of minimum spanning trees for all connected components).
Size of the output data: [math]O(|V|)[/math].
1.10 Properties of the algorithm
- The algorithm terminates in a finite number of steps because, at each step, the number of fragments reduces by at least one.
- Moreover, the number of fragments at least halves at each step; consequently, the total number of steps is at most [math]\log_2 n[/math]. This implies an estimate for the complexity of the algorithm.
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
2.2 Possible methods and considerations for parallel implementation of the algorithm
A program implementing Borůvka's algorithm consists of two parts:
1. the part that is responsible for the general coordination of computations;
2. the part that is responsible for the parallel computations on a multi-core CPU or GPU.
The serial algorithm described above cannot be used in a parallel program: in an implementation of [math]MERGE[/math], the results of operations [math]FIND(u)[/math] and [math]FIND(v)[/math] may permanently vary, which results in a race condition. A parallel variant of the algorithm is described in paper
1. Each vertex v is assigned the record [math]A[v] = { parent, rank }[/math]. At first, [math]A[v] := { v, 0 }[/math].
2. The auxiliary operation [math]UPDATE(v, rank_v, u, rank_u)[/math]:
old := A[v]
if old.parent != v or old.rank != rank_v then return false
new := { u, rank_u }
return CAS(A[v], old, new)
3. The operation [math]FIND(v)[/math]:
while v != A[v].parent do
u := A[v].parent
CAS(A[v].parent, u, A[u].parent)
v := A[u].parent
return v
4. The operation UNION(u, v):
while true do
(u, v) := (FIND(u), FIND(v))
if u = v then return false
(rank_u, rank_v) := (A[u].rank, A[v].rank)
if (A[u].rank, u) > (A[v].rank, v) then
swap((u, rank_u), (v, rank_v))
if UPDATE(u, rank_u, v, rank_u) then
if rank_u = rank_v then
UPDATE(v, rank_v, v, rank_v + 1)
return true
This variant of the algorithm is guaranteed to have the "wait-free" property. In practice, one may use a simplified version with no count of ranks. It has a weaker "lock-free" property but, in a number of cases, wins in speed.