Difference between revisions of "Dot product"
| [unchecked revision] | [checked revision] |
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{level-a}} | |
| − | + | Primary authors of this description: [[:ru:Участник:Frolov|A.V.Frolov]]. | |
| − | == | + | == Properties and structure of the algorithm == |
| − | + | === General description of the algorithm === | |
| − | + | '''The dot product of vectors''' is one of the basic operations in a number of methods. It is used in two versions: as the proper dot product of <math>n</math>-dimensional vectors (one-dimensional arrays of size <math>n</math>) and as the scalar product of rows, columns, and other linear subsets of multidimensional arrays. The latter differs from the former in that the corresponding subroutine receives not only the initial addresses of vectors but also parameters of the displacement of the subsequent components with respect to the preceding ones (for the former version, all the displacements are equal to one). Formulas defining the dot product are different for real and complex arithmetic. Here, we deal only with real arithmetic and the serial-parallel implementation. | |
| − | + | === Mathematical description of the algorithm === | |
| − | + | Input data: two one-dimensional numeric arrays of size n. | |
| − | + | Output data: the sum of pairwise products of the corresponding elements of both arrays. | |
| − | + | ||
| + | Formulas of the method: | ||
| + | the number <math>n</math> is expressed in the form | ||
<math>n = (p - 1) k + q</math>, | <math>n = (p - 1) k + q</math>, | ||
| − | + | where <math>p</math> is the number of processors, <math>k = \lceil \frac{n}{p} \rceil</math>, and | |
| − | <math>q = n - k (p - 1)</math>. | + | <math>q = n - k (p - 1)</math>. Then the <math>i</math>-th processor (<math>i < p</math>) calculates in the serial mode the partial dot product of the subarrays formed of the elements with indices from <math>(i - 1) k + 1</math> to <math>ik</math>. |
| − | |||
:<math>S_i = \sum_{j = 1}^k a_{k (i - 1) + j} b_{k (i - 1) + j}</math> | :<math>S_i = \sum_{j = 1}^k a_{k (i - 1) + j} b_{k (i - 1) + j}</math> | ||
| − | + | The <math>p</math>-th processor calculates in the serial mode the partial dot product of the subarrays formed of the elements with indices from <math>(p - 1) k + 1</math> to <math>(p - 1) k + q</math>. | |
:<math>S_p = \sum_{j = 1}^q a_{k (p - 1) + j} b_{k (p - 1) + j}</math> | :<math>S_p = \sum_{j = 1}^q a_{k (p - 1) + j} b_{k (p - 1) + j}</math> | ||
| − | + | Upon ending this process, the processors exchange their data, and then one of them (or all of them simultaneously if they need the result later on) add the partial sums in the serial mode. | |
:<math>\sum_{i = 1}^p S_i</math> | :<math>\sum_{i = 1}^p S_i</math> | ||
| − | + | In the serial-parallel version, all the sums are calculated in the serial mode (usually in the increasing order of indices). | |
| − | === | + | === Computational kernel of the algorithm === |
| − | + | The computational kernel of the dot product in the serial-parallel version can be represented as <math>p</math> calculations of partial dot products with the subsequent serial summation of <math>p</math> partial results. | |
| − | === | + | === Macro structure of the algorithm === |
| − | + | As already noted in the description of the kernel, the basic part of the algorithm consists of the parallel computation of partial dot products, calculated in the serial mode, and the subsequent summation of these partial dot products. | |
| − | === | + | === Implementation scheme of the serial algorithm === |
| − | + | The formulas of the method are given above. The order of summation can be different, both in the increasing and decreasing order of indices. If no special reason is pursued, then, usually, the natural order of increasing indices is used. | |
| − | === | + | === Serial complexity of the algorithm === |
| − | + | In any implementation of the dot product for arrays consisting of <math>n</math> elements the number of scalar multiplications is invariably equal to <math>n</math>, while the number of additions is <math>n - 1</math>. Consequently, in terms of the number of serial operations, the algorithm should be qualified as a ''linear'' complexity algorithm. | |
| − | === | + | === Information graph === |
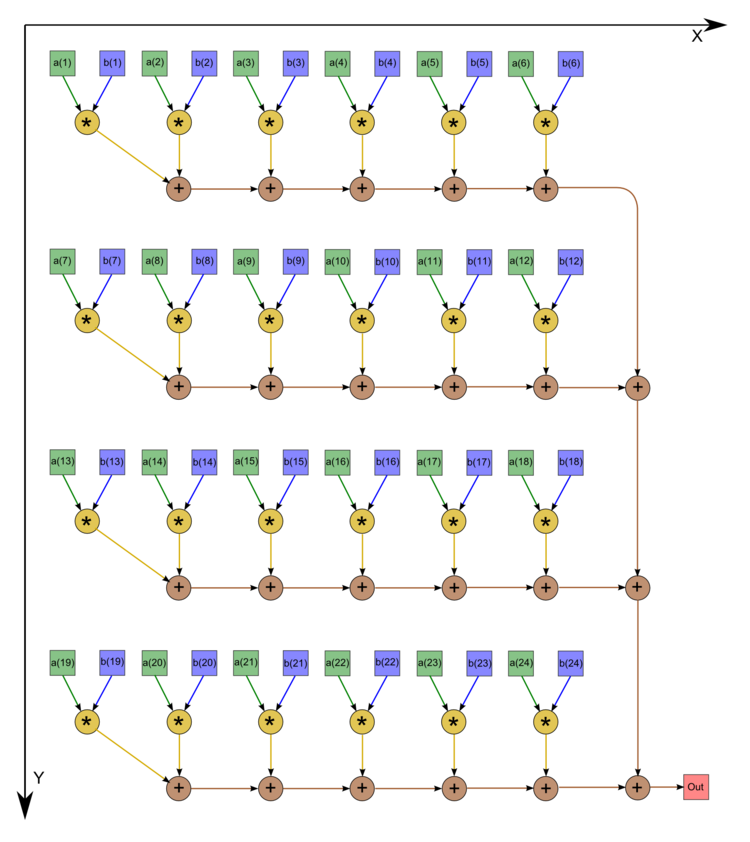
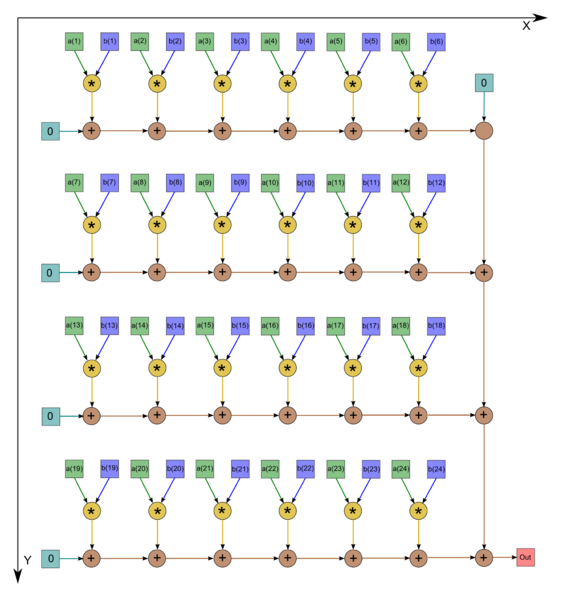
| − | + | We describe the graph of the algorithm graphically (see the first figure). It should be noted, however, that, in most cases, programmers prefer to assign zero initial values to variables chosen for summation, which increases the number of additions by one. In such cases, the graph is as shown in the second figure (n=24). | |
{| align="left" | {| align="left" | ||
|- valign="top" | |- valign="top" | ||
| − | | [[file:series- | + | | [[file:series-parallel_dot_product_graph.png|thumb|750px|Figure 1. Serial-parallel calculation of the dot product with saving in the number of additions]] |
| − | | [[file:Series- | + | | [[file:Series-parallel_dot_product_graph_straight.png|thumb|790px|Figure 2. Serial-parallel calculation of the dot product without saving in the number of additions]] |
|} | |} | ||
| − | === | + | === Parallelization resource of the algorithm === |
| + | |||
| + | The parallel version of the serial-parallel method for calculating the dot product of arrays of size <math>n</math> requires that the following layers be successively executed: | ||
| + | * 1 layer of calculating pairwise products, | ||
| + | * <math>k - 1</math> layers of summation for partial dot products (<math>p</math> branches), | ||
| + | * <math>p - 1</math> layers of summation (one serial branch). | ||
| + | |||
| + | Therefore, the critical path of the algorithm in the parallel version (and the corresponding height of the CPF) depends on the chosen partition of the arrays. In the optimal case (<math>p = \sqrt{n}</math>), the height of the CPF is <math> 2 \sqrt{n} - 1</math>. Thus, in terms of the height of the CPF, the serial-parallel method is qualified as a square-root complexity algorithm. In terms of the width of the CPF, it is also a square-root complexity algorithm. | ||
| + | |||
| + | === Input and output data of the algorithm === | ||
| + | |||
| + | Input data: array<math>a</math> (with elements <math>a_i</math>), array <math>b</math> (with elements <math>b_i</math>). | ||
| + | |||
| + | Further restrictions: none. | ||
| + | |||
| + | Size of the input data: <nowiki/><math>2 n</math>. | ||
| + | |||
| + | Output data: the sum of pairwise products of the corresponding elements of two arrays. | ||
| + | |||
| + | Size of the output data: single scalar. | ||
| + | |||
| + | === Properties of the algorithm === | ||
| + | |||
| + | It is clear that, in the case of unlimited resources, the ratio of the serial to parallel complexity is expressed by the ''square root'' of n (since this is the ratio of the linear to square-root complexity). The computational power of the algorithm, understood as the ratio of the number of operations to the total size of the input and output data, is only ''1 (the size of the input and output data is almost equal to the number of operations; more exactly, the former number exceeds the latter by 2)''. For a given partition of <math>n</math>, the algorithm is completely determined. The edges of the information graph are local. In a number of algorithms using dot products of single precision and the accumulation mode, these products are calculated in double precision in order to reduce round-off errors. However, even without accumulation mode, the serial-parallel method for calculating the dot product reduces the effect of round-off errors <math>\sqrt{n}</math>-fold "on the average". | ||
| − | + | == Software implementation of the algorithm == | |
| − | |||
| − | |||
| − | |||
| − | + | === Implementation peculiarities of the serial algorithm === | |
| − | + | The simplest variation (without a summation inversion) in Fortran can be written as follows: | |
| − | + | <source lang="fortran"> | |
| + | DO I = 1, P | ||
| + | S (I) = A(K*(I-1)+1)*B(K*(I-1)+1) | ||
| + | IF (I.LQ.P) THEN | ||
| + | DO J = 2,K | ||
| + | S(I)=S(I)+A(K*(I-1)+J)*B(K*(I-1)+J) | ||
| + | END DO | ||
| + | ELSE | ||
| + | DO J = 2,Q | ||
| + | S(I)=S(I)+A(K*(I-1)+J)*B(K*(I-1)+J) | ||
| + | END DO | ||
| + | END IF | ||
| + | END DO | ||
| + | SCP = S(1) | ||
| + | DO I = 2, P | ||
| + | SCP = SCP + S(I) | ||
| + | END DO | ||
| + | </source> | ||
| − | + | Similar versions can be written with an inverted summation. It should be noted that the algorithm chart [[#Information graph|is the same for both versions]]! The initial cycle body as a whole can be replaced with a call to the scalar product function, if its serial version has been implemented. | |
| − | + | === Possible methods and considerations for parallel implementation of the algorithm === | |
| − | + | In addition to [[#Implementation peculiarities of the sequential algorithm|the simplest implementation described above]], there are more complex codes for implementing the same algorithm. It should be noted that a number of the implementations (in the same BLAS) use the decomposition of <math>n</math> into a small and large number. In this case, nested cycles are not used, as the summation of a small number of multiplication operations is performed “manually” by expanding the initial cycle. Some implementations of the serial-parallel computation method are not written as individual subprograms, but scattered around the code producing scalar multiplication, despite effectively representing this kind of implementation. Examples of this approach include block implementations of various decompositions (Cholesky decomposition, Gaussian decomposition, etc.). | |
| − | + | === Run results === | |
| + | === Conclusions for different classes of computer architecture === | ||
| − | == | + | == References == |
| − | + | <references /> | |
| − | [[Category: | + | [[Category:Finished articles]] |
[[Ru:Скалярное произведение векторов, вещественная версия, последовательно-параллельный вариант]] | [[Ru:Скалярное произведение векторов, вещественная версия, последовательно-параллельный вариант]] | ||
Latest revision as of 14:49, 8 July 2022
Primary authors of this description: A.V.Frolov.
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
The dot product of vectors is one of the basic operations in a number of methods. It is used in two versions: as the proper dot product of [math]n[/math]-dimensional vectors (one-dimensional arrays of size [math]n[/math]) and as the scalar product of rows, columns, and other linear subsets of multidimensional arrays. The latter differs from the former in that the corresponding subroutine receives not only the initial addresses of vectors but also parameters of the displacement of the subsequent components with respect to the preceding ones (for the former version, all the displacements are equal to one). Formulas defining the dot product are different for real and complex arithmetic. Here, we deal only with real arithmetic and the serial-parallel implementation.
1.2 Mathematical description of the algorithm
Input data: two one-dimensional numeric arrays of size n.
Output data: the sum of pairwise products of the corresponding elements of both arrays.
Formulas of the method: the number [math]n[/math] is expressed in the form [math]n = (p - 1) k + q[/math], where [math]p[/math] is the number of processors, [math]k = \lceil \frac{n}{p} \rceil[/math], and [math]q = n - k (p - 1)[/math]. Then the [math]i[/math]-th processor ([math]i \lt p[/math]) calculates in the serial mode the partial dot product of the subarrays formed of the elements with indices from [math](i - 1) k + 1[/math] to [math]ik[/math].
- [math]S_i = \sum_{j = 1}^k a_{k (i - 1) + j} b_{k (i - 1) + j}[/math]
The [math]p[/math]-th processor calculates in the serial mode the partial dot product of the subarrays formed of the elements with indices from [math](p - 1) k + 1[/math] to [math](p - 1) k + q[/math].
- [math]S_p = \sum_{j = 1}^q a_{k (p - 1) + j} b_{k (p - 1) + j}[/math]
Upon ending this process, the processors exchange their data, and then one of them (or all of them simultaneously if they need the result later on) add the partial sums in the serial mode.
- [math]\sum_{i = 1}^p S_i[/math]
In the serial-parallel version, all the sums are calculated in the serial mode (usually in the increasing order of indices).
1.3 Computational kernel of the algorithm
The computational kernel of the dot product in the serial-parallel version can be represented as [math]p[/math] calculations of partial dot products with the subsequent serial summation of [math]p[/math] partial results.
1.4 Macro structure of the algorithm
As already noted in the description of the kernel, the basic part of the algorithm consists of the parallel computation of partial dot products, calculated in the serial mode, and the subsequent summation of these partial dot products.
1.5 Implementation scheme of the serial algorithm
The formulas of the method are given above. The order of summation can be different, both in the increasing and decreasing order of indices. If no special reason is pursued, then, usually, the natural order of increasing indices is used.
1.6 Serial complexity of the algorithm
In any implementation of the dot product for arrays consisting of [math]n[/math] elements the number of scalar multiplications is invariably equal to [math]n[/math], while the number of additions is [math]n - 1[/math]. Consequently, in terms of the number of serial operations, the algorithm should be qualified as a linear complexity algorithm.
1.7 Information graph
We describe the graph of the algorithm graphically (see the first figure). It should be noted, however, that, in most cases, programmers prefer to assign zero initial values to variables chosen for summation, which increases the number of additions by one. In such cases, the graph is as shown in the second figure (n=24).
1.8 Parallelization resource of the algorithm
The parallel version of the serial-parallel method for calculating the dot product of arrays of size [math]n[/math] requires that the following layers be successively executed:
- 1 layer of calculating pairwise products,
- [math]k - 1[/math] layers of summation for partial dot products ([math]p[/math] branches),
- [math]p - 1[/math] layers of summation (one serial branch).
Therefore, the critical path of the algorithm in the parallel version (and the corresponding height of the CPF) depends on the chosen partition of the arrays. In the optimal case ([math]p = \sqrt{n}[/math]), the height of the CPF is [math] 2 \sqrt{n} - 1[/math]. Thus, in terms of the height of the CPF, the serial-parallel method is qualified as a square-root complexity algorithm. In terms of the width of the CPF, it is also a square-root complexity algorithm.
1.9 Input and output data of the algorithm
Input data: array[math]a[/math] (with elements [math]a_i[/math]), array [math]b[/math] (with elements [math]b_i[/math]).
Further restrictions: none.
Size of the input data: [math]2 n[/math].
Output data: the sum of pairwise products of the corresponding elements of two arrays.
Size of the output data: single scalar.
1.10 Properties of the algorithm
It is clear that, in the case of unlimited resources, the ratio of the serial to parallel complexity is expressed by the square root of n (since this is the ratio of the linear to square-root complexity). The computational power of the algorithm, understood as the ratio of the number of operations to the total size of the input and output data, is only 1 (the size of the input and output data is almost equal to the number of operations; more exactly, the former number exceeds the latter by 2). For a given partition of [math]n[/math], the algorithm is completely determined. The edges of the information graph are local. In a number of algorithms using dot products of single precision and the accumulation mode, these products are calculated in double precision in order to reduce round-off errors. However, even without accumulation mode, the serial-parallel method for calculating the dot product reduces the effect of round-off errors [math]\sqrt{n}[/math]-fold "on the average".
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
The simplest variation (without a summation inversion) in Fortran can be written as follows:
DO I = 1, P
S (I) = A(K*(I-1)+1)*B(K*(I-1)+1)
IF (I.LQ.P) THEN
DO J = 2,K
S(I)=S(I)+A(K*(I-1)+J)*B(K*(I-1)+J)
END DO
ELSE
DO J = 2,Q
S(I)=S(I)+A(K*(I-1)+J)*B(K*(I-1)+J)
END DO
END IF
END DO
SCP = S(1)
DO I = 2, P
SCP = SCP + S(I)
END DO
Similar versions can be written with an inverted summation. It should be noted that the algorithm chart is the same for both versions! The initial cycle body as a whole can be replaced with a call to the scalar product function, if its serial version has been implemented.
2.2 Possible methods and considerations for parallel implementation of the algorithm
In addition to the simplest implementation described above, there are more complex codes for implementing the same algorithm. It should be noted that a number of the implementations (in the same BLAS) use the decomposition of [math]n[/math] into a small and large number. In this case, nested cycles are not used, as the summation of a small number of multiplication operations is performed “manually” by expanding the initial cycle. Some implementations of the serial-parallel computation method are not written as individual subprograms, but scattered around the code producing scalar multiplication, despite effectively representing this kind of implementation. Examples of this approach include block implementations of various decompositions (Cholesky decomposition, Gaussian decomposition, etc.).