Cholesky decomposition, SCALAPACK
Primary author of this description: Alexey Teplov (Section 4).
Contents
1 Links
For our experiments we used the ScaLAPACK implementation for the Cholesky decomposition from the MKL library (the pdpotrf method).
2 Locality of data and computations
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
2.1.2 Quantitative estimation of locality
3 Scalability of the algorithm and its implementations
3.1 Scalability of the algorithm
3.2 Scalability of of the algorithm implementation
4 Dynamic characteristics and efficiency of the algorithm implementation
All results were obtained on the "Lomonosov" supercomputer[1] installed at the Research Computing Center of Moscow State University. For the experiments we used the Intel Xeon X5570 processors with 94 Gflops peak performance and the Intel compiler with -O2 option.
The figures below illustrate the Cholesky decomposition implementation efficiency (the case of lower triangular matrices) for the matrix order 80000 and 256 processes.
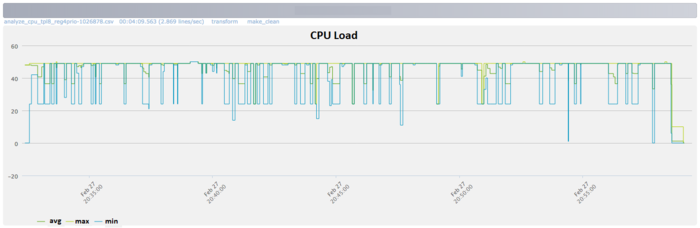
Fig.1 shows that, during the runtime of the program, the processor usage level is about 50%. That is a good result for programs executed without the usage of the Hyper Threading technology.
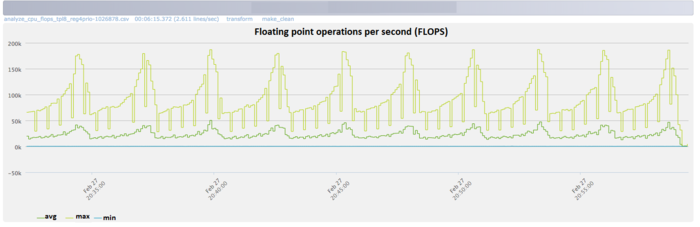
Fig.2 shows the number of floating point operations per second during the Cholesky decomposition exection time. To the end of each iteration, the number of opertations increases intensively.
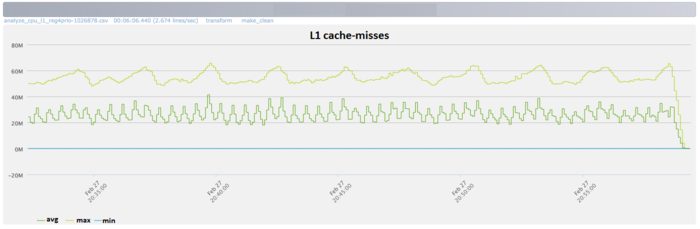
From Fig.3 it follows that the number of L1 cache-misses is large enough (about 25 millions per second on the average for all nodes).
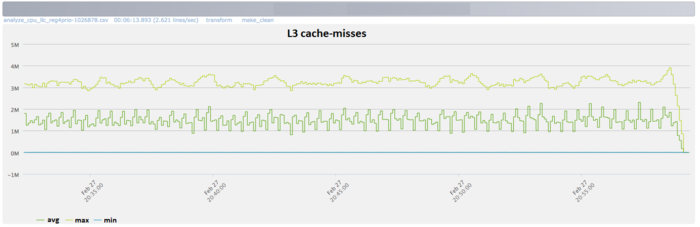
From Fig.4 it follows that the number of L3 cache-misses is still large (about 1.5 millions/second). This fact indicates that the matrix order is large and the data do not fit in the cache.
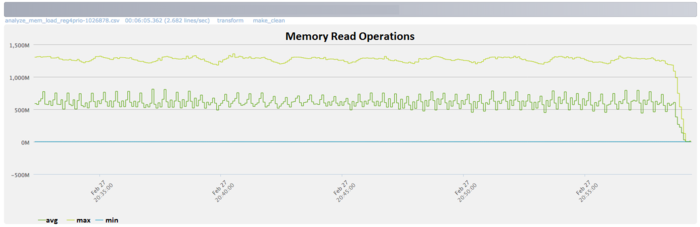
From Fig.5 it follows that, during the execution time, the memory access is intensive enough and remains on approximately the same level.
From Fig.6 it follows that, to the end of each iteration, the number of memory write operations decreases rather considerably. This situation corelates with the increase in the number of floating point operations and can be explained by the fact the overheads are reduced and the efficiency increases when the number of memory write operations decreases.
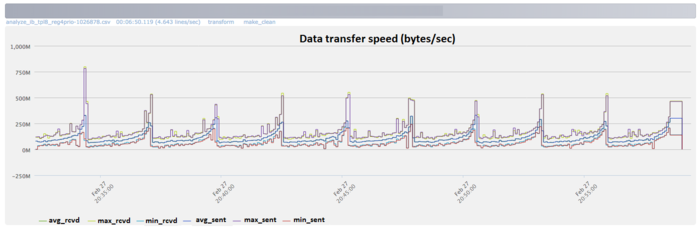
From Fig.7 follows that the communication network is intensively used at each interation. To the end of each iteration, the data transfer intensity increases significantly. This fact indicates that, to the end of each iteration, the data exchange increases among the processes.
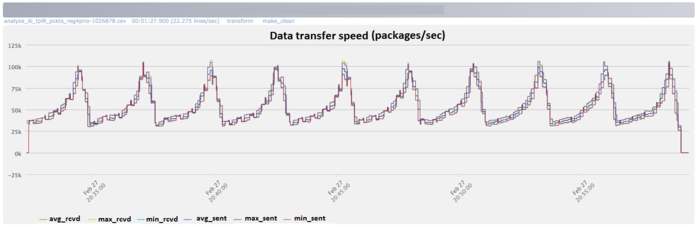
The Infiniband data transfer rate in packets per second shows a relatively uniform dispersion of maximum, minimum and average values compared to the bytes-per-second diagram. This shows that the processes are probably exchanging messages of varying lengths: an indication of unevenly distributed data. Network utilization is also intensified by the end of each iteration.
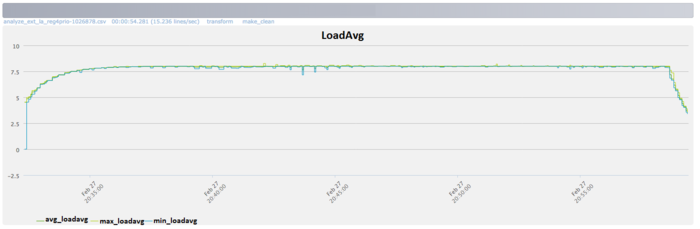
Fig.9 shows that the number of processes ready for the execution (LoadAvg) remains constant and is equal to 8 throughout the program run. This shows that the program is operating in a stable manner, with eight processes on each node. When the octa-core computing nodes are used, this indicates a rational and static loading of hardware resources by computing processes.
Overall, the data obtained from the monitoring system allows one to come to the conclusion that the program under study was working in an efficient and stable manner. The memory and communication environment usage is intensive, which can lead to an efficiency reduction with an increase of the matrix order or the number of processors in use.
5 Run results
6 References
- ↑ Voevodin Vl.V., Zhumatii S.A., Sobolev S.I., Antonov A.S., Bryzgalov P.A., Nikitenko D.A., Stefanov K.S., Voevodin Vad.V. The Lomonosov supercomputer in practice. Otkrytye Sistemy (2012) No. 7, 36-39.