Bellman-Ford algorithm
| Алгоритм Беллмана-Форда | |
| Sequential algorithm | |
| Serial complexity | [math]O(|V||E|)[/math] |
| Input data | [math]O(|V| + |E|)[/math] |
| Output data | [math]O(|V|^2)[/math] |
| Parallel algorithm | |
| Parallel form height | [math]N/A, max O(|V|) [/math] |
| Parallel form width | [math]O(|E|)[/math] |
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 2.1 Implementation peculiarities of the serial algorithm
- 2.2 Locality of data and computations
- 2.3 Possible methods and considerations for parallel implementation of the algorithm
- 2.4 Scalability of the algorithm and its implementations
- 2.5 Dynamic characteristics and efficiency of the algorithm implementation
- 2.6 Conclusions for different classes of computer architecture
- 2.7 Existing implementations of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
The Bellman-Ford algorithm[1][2][3] was designed for finding the shortest paths between nodes in a graph. For a given weighted digraph, the algorithm finds the shortest paths between a singled-out source node and the other nodes of the graph. The Bellman-Ford algorithm scales worse than other algorithms for solving this problem (the complexity is [math]O(|V||E|)[/math] against [math]O(|E| + |V|\ln(|V|))[/math] for Dijkstra's algorithm). However, its distinguishing feature is the applicability to graphs with arbitrary (including negative) weights.
1.2 Mathematical description of the algorithm
Let [math]G = (V, E)[/math] be a given graph with arc weights [math]f(e)[/math] f(e) and the single-out source node [math]u[/math]. Denote by [math]d(v)[/math] the shortest distance between the source node [math]u[/math] and the node [math]v[/math].
The Bellman-Ford algorithm finds the value [math]d(v)[/math] as the unique solution to the equation
- [math] d(v) = \min \{ d(w) + f(e) \mid e = (w, v) \in E \}, \quad \forall v \ne u, [/math]
with the initial condition [math]d(u) = 0[/math].
1.3 Computational kernel of the algorithm
The algorithm is based on the principle of arc relaxation: if [math]e = (w, v) \in E[/math] and [math]d(v) \gt d(w) + f(e)[/math], then the assignment [math]d(v) \leftarrow d(w) + f(e)[/math] is performed.
1.4 Macro structure of the algorithm
The algorithm successively refines the values of the function [math]d(v)[/math].
- At the very start, the assignment [math]d(u) = 0[/math], [math]d(v) = \infty[/math], [math]\forall v \ne u[/math] is performed.
- Then [math]|V|-1[/math] iteration steps are executed. At each step, all the arcs of the graph undergo the relaxation.
The structure of the algorithm can be described as follows:
1. Initialization: all the nodes are assigned the expected distance [math]t(v)=\infty[/math]. The only exception is the source node for which [math]t(u)=0[/math] .
2. Relaxation of the set of arcs [math]E[/math]:
(a) For each arc [math]e=(v,z) \in E[/math], the new expected distance is calculated: [math]t^' (z)=t(v)+ w(e)[/math].
(b) If [math]t^' (z)\lt t(z)[/math], then the assignment [math]t(z) := t' (z)[/math] (relaxation of the arc [math]e[/math]) is performed.
3. The algorithm continues to work as long as at least one arc undergoes relaxation.
Suppose that the relaxation of some arcs was still performed at the [math]|V|[/math]-th iteration step. Then the graph contains a cycle of negative length. An arc [math]e=(v,z)[/math] lying on such cycle can be found by testing the condition [math]t(v)+w(e)\lt d(z)[/math] (this condition can be verified for all the arcs in linear time).
1.5 Implementation scheme of the serial algorithm
The serial algorithm is implemented by the following pseudo-code:
Input data:
graph with nodes V and arcs E with weights f(e);
source node u.
Output data: distances d(v) from the source node u to each node v ∈ V.
for each v ∈ V do d(v) := ∞
d(u) = 0
for i from 1 to |V| - 1:
for each e = (w, v) ∈ E:
if d(v) > d(w) + f(e):
d(v) := d(w) + f(e)
1.6 Serial complexity of the algorithm
The algorithm performs [math]|V|-1[/math] iteration steps; at each step, [math]|E|[/math] arcs are relaxed. Thus, the total work is [math]O(|V||E|)[/math] operations.
The constant in the complexity estimate can be reduced by using the following two conventional techniques:
- Algorithm terminates if no successful relaxation occurred at the current iteration step.
- At the current step, not all the arcs are inspected but only the arcs outgoing from nodes that were involved in successful relaxations at the preceding step. (At the first step, only the arcs outgoing from the source node are examined.)
1.7 Information graph
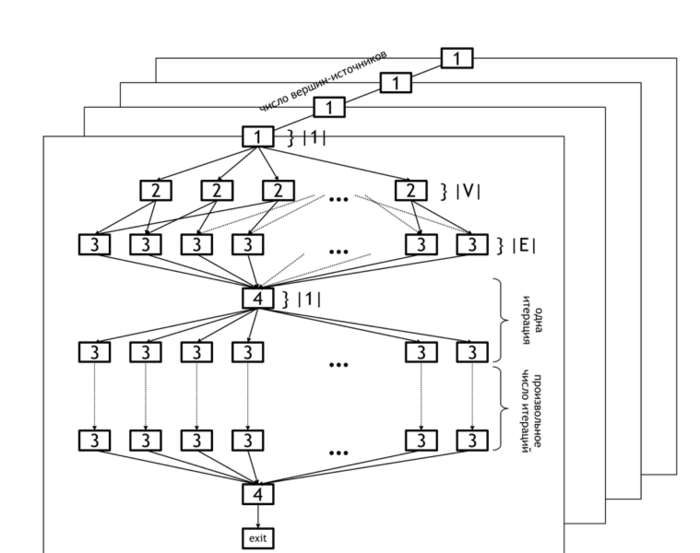
The information graph of the Bellman-Ford algorithm is shown in figure 1. It demonstrates the levels of parallelism in this algorithm.
The lower level of parallelism refers to operations executed within each horizontal plane. The set of all planes represents the upper level of parallelism (because operations in different planes can be carried out concurrently).
The lower level of parallelism in the algorithm graph corresponds to levels [2] and [3], which represent the operations of initialization of the distance array ([2]) and updating of this array based on the data in arcs array ([3]). Operation [4] refers to the test whether any changes occurred at the current iteration and the loop termination if no changes were done.
As already said, the upper level of parallelism consists in the parallel calculation of distances for different source nodes. In the figure, it is illustrated by the set of distinct planes.
1.8 Parallelization resource of the algorithm
The Bellman-Ford algorithm has a considerable parallelization resource. First, the search for shortest paths can be independently performed for all the nodes (parallel vertical planes in figure 1). Second, the search for shortest paths beginning in a fixed node [math]u[/math] can also be made in parallel: the initialization of the original paths ([2]) requires [math]|V|[/math] parallel operations, and the relaxation of all arcs costs [math]O(|E|)[/math] parallel operations.
Thus, if [math]O(|E|)[/math] processors are available, then the algorithm terminates after at most [math]|V|[/math] steps. Actually, a smaller number of steps are usually required, namely, [math]O(r)[/math] steps. (This number is the maximum length of the shortest paths outgoing from the chosen source node [math]u[/math]).
It follows that the width of the parallel form of the Bellman-Ford algorithm is [math]O(|E|)[/math], while its height is [math]O(r) | r \lt |V|[/math].
The algorithm of Δ-stepping can be regarded as a parallel version of the Bellman-Ford algorithm.
1.9 Input and output data of the algorithm
Input data: weighted graph [math](V, E, W)[/math] ([math]|V|[/math] nodes [math]v_i[/math] and [math]|E|[/math] arcs [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math] with weights [math]f_j[/math]), source node [math]u[/math].
Size of input data: [math]O(|V| + |E|)[/math].
Output data (возможные варианты):
- для каждой вершины [math]v[/math] исходного графа – последнее ребро [math]e^*_v = (w, v)[/math], лежащее на кратчайшем пути от вершины [math]u[/math] к [math]v[/math], или соответствующая вершина [math]w[/math];
- для каждой вершины [math]v[/math] исходного графа – суммарный вес [math]f^*(v)[/math] кратчайшего пути от от вершины [math]u[/math] к [math]v[/math].
Size of output data: [math]O(|V|)[/math].
1.10 Properties of the algorithm
Алгоритм может распознавать наличие отрицательных циклов в графе. Ребро [math]e = (v, w)[/math] лежит на таком цикле, если вычисленные алгоритмом кратчайшие расстояния [math]d(v)[/math] удовлетворяют условию
- [math] d(v) + f(e) \lt d(w), [/math]
где [math]f(e)[/math] – вес ребра [math]e[/math]. Условие может быть проверено для всех рёбер графа за время [math]O(|E|)[/math].
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
2.2 Locality of data and computations
2.2.1 Locality of implementation
2.2.1.1 Structure of memory access and a qualitative estimation of locality
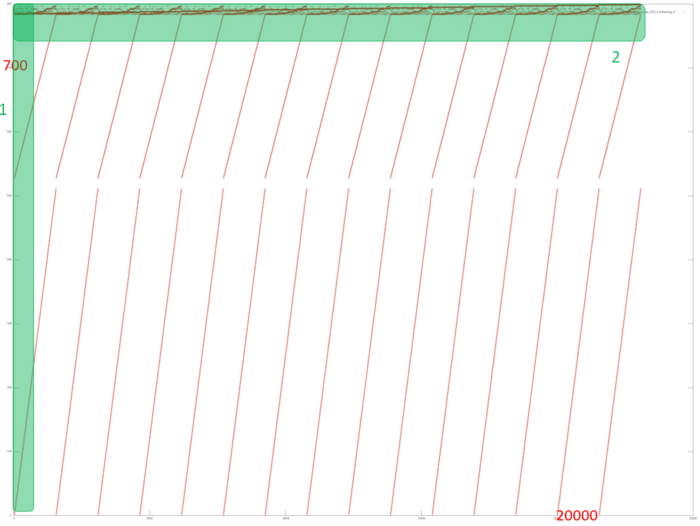
На рис. 2 представлен профиль обращений в память для реализации алгоритма Беллмана-Форда. Первое, что сразу стоит отметить – число обращений в память гораздо больше числа задействованных данных. Это говорит о частом повторном использовании одних и тех же данных, что обычно приводит к высокой временной локальности. Далее, видна явная регулярная структура производимых обращений в память, видны повторяющиеся итерации работы алгоритма. Практически все обращения образуют фрагменты, похожие на последовательный перебор, кроме самой верхней части, где наблюдается более сложная структура.
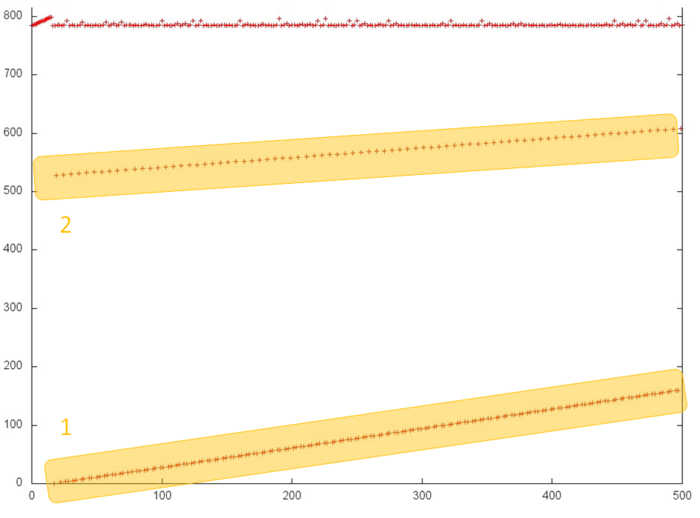
Рассмотрим более детально отдельные фрагменты общего профиля, чтобы лучше разобраться в его структуре. На рис. 3 представлен фрагмент 1 (выделен на рис. 2), на котором показаны первые 500 обращений в память (отметим, что другой наклон двух последовательных переборов связан с измененным отношением сторон в рассматриваемой области). Данный рисунок показывает, что выделенные желтым части 1 и 2 являются практические идентичными последовательными переборами; отличие между ними только в том, что в части 1 обращения выполняются в два раза чаще, поэтому на рис. 3 эта часть представлена большим числом точек. Как мы знаем, подобные профили характеризуются высокой пространственной и низкой временной локальностью.
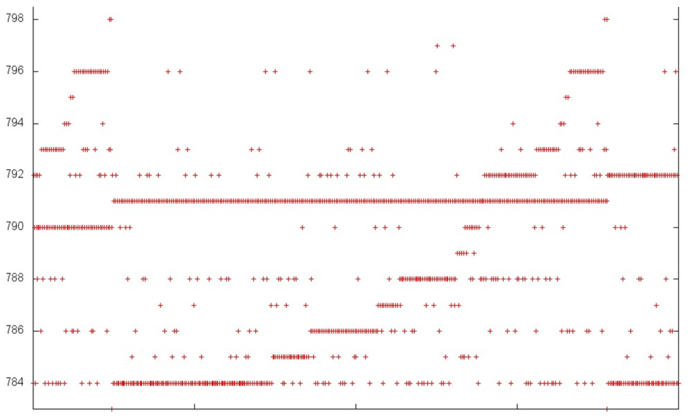
Далее рассмотрим более интересный фрагмент 2, отмеченный на рис. 2 (см. рис. 4). Здесь можно снова увидеть подтверждение регулярности обращений в нижней области профиля, однако верхняя область явно устроена гораздо сложнее; хотя и здесь просматривается регулярность. В частности, также видны те же самые итерации, в которых здесь можно выделить большие последовательности обращений к одним и тем же данным. Пример такого поведения, оптимального с точки зрения локальности, выделен на рисунке желтым.
Чтобы понять структуру обращений в память в верхней части, можно рассмотреть ее еще подробнее. Приведем визуализацию небольшой области фрагмента 1, выделенную на рис. 4 зеленым. Однако в данном случае дальнейшее приближение (рис. 5) не привносит большей ясности: видна нерегулярная структура внутри итерации, характер которой достаточно сложно описать. Но в данном случае этого и не требуется – можно заметить, что по вертикали отложено всего 15 элементов, при этом обращений к ним выполняется гораздо больше. Независимо от структуры обращений, такой профиль обладает очень высокой как пространственной, так и временной локальностью.
А так как основная масса обращений приходится именно на фрагмент 2, можно утверждать, что и весь общий профиль обладает высокой пространственной и временной локальностью.
2.2.1.2 Quantitative estimation of locality
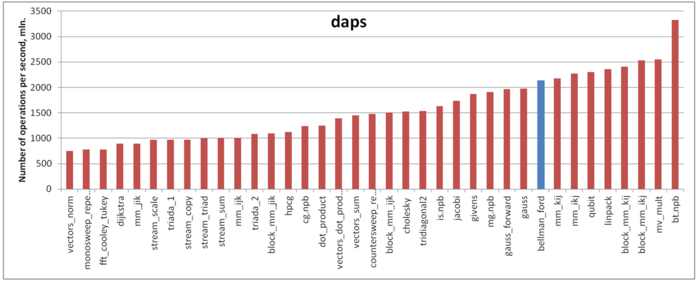
Оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рисунке 6 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что по производительности работы с памятью данная реализация алгоритма показывает очень хорошие результаты. В частности, значение daps сравнимо с оценкой для теста Linpack, который известен высокой эффективностью взаимодействия с подсистемой памяти.
2.3 Possible methods and considerations for parallel implementation of the algorithm
Программа, реализующая алгоритм поиска кратчайших путей, состоит из двух частей: части, отвечающей за общую координацию вычислений, а так же параллельные вычисления на многоядерных CPU, и GPU части, отвечающей только за вычисления на графическом ускорителе.
2.4 Scalability of the algorithm and its implementations
2.4.1 Scalability of the algorithm
Алгоритм обладает значительным потенциалом масштабируемости, так как каждое ребро обрабатывается независимо и можно поручить каждому вычислительному процессу свою часть рёбер графа. Узким местом является доступ к разделяемому всеми процессами массиву расстояний. Алгоритм позволяет ослабить требования к синхронизации данных этого массива между процессами (когда один процесс может не сразу увидеть новое значение расстояния, записанное другим процессом), за счёт, может быть, большего количества глобальных итераций.
2.4.2 Scalability of of the algorithm implementation
Проведём исследование масштабируемости параллельной реализации алгоритма Беллмана-Форда согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов-2 Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [1 : 28] с шагом 1;
- размер графа [2^20 : 2^27].
Проведем отдельные исследования сильной масштабируемости вширь реализации алгоритма Беллмана-Форда.
Производительность определена как TEPS (от англ. Traversed Edges Per Second), то есть число ребер графа, который алгоритм обрабатывает в секунду. С помощью данной метрики можно сравнивать производительность для различных размеров графа, оценивая, насколько понижается эффективность обработки графа при увеличении его размера.
2.5 Dynamic characteristics and efficiency of the algorithm implementation
Для проведения экспериментов использовалась реализация алгоритма Беллмана-Форда, реализованная для CPU. Все результаты получены на суперкомпьютере «Ломоносов-2». Использовались процессоры Intel Xeon E5-2697v3, задача решалась для графа большого размера на одном узле. На рисунках показана эффективность реализации алгоритма Беллмана-Форда, запуск проводился на 1 узле для графа 2^27, выполнялась 1 итерация.
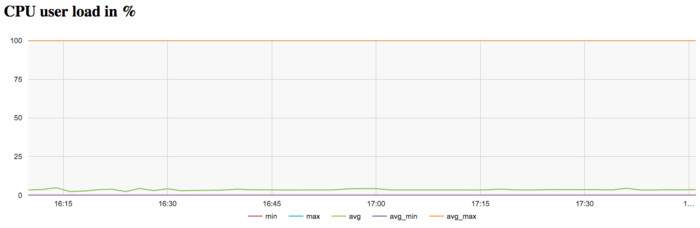
На графике загрузки процессора видно, что почти все время работы программы не загружены и средний уровень загрузки составляет около 5%. Это достаточно неэффективная картина даже для программ, запущенных c использованием одного ядра в реализации.
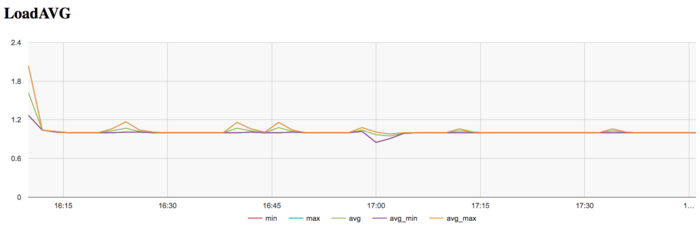
На графике числа процессов, ожидающих вхождения в стадию счета (Loadavg), видно, что на протяжении всей работы программы значение этого параметра постоянно на уровне 1. Это указывает на постоянную загрузку аппаратных ресурсов не более чем 1 процессом, однако их число для узла слишком мало, что с одной стороны может указывать на не очень рациональные использование ресурсов.
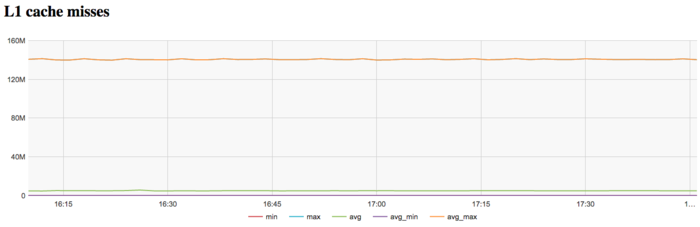
На графике кэш-промахов первого уровня видно, что число промахов очень высокое и находится на уровне 140 млн/сек это очень высокий показатель, показывающие потенциальную причину неэффективности.
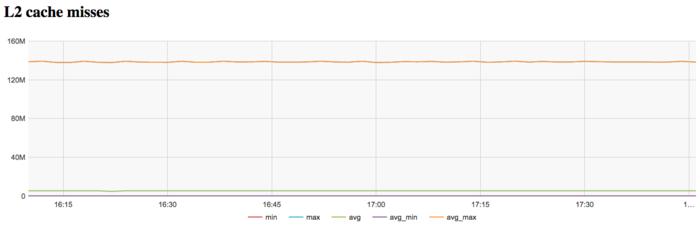
На графике кэш-промахов второго уровня видно, что число промахов достаточно тоже крайне высокое и находится на уровне 140 млн/сек, что указывает на крайне неэффективную работу с памятью.
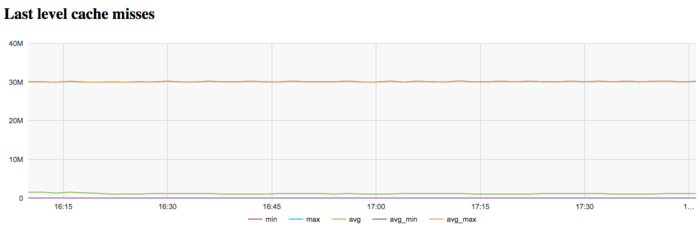
На графике кэш-промахов последнего уровня видно, что число промахов тоже достаточно большое и составляет около 30 млн/сек по всем узлам. Это указывает на то, что задача очень плохо укладывается в кэш-память, и программа постоянно работает с оперативной памятью, что объясняется очень большим размером использованного графа.
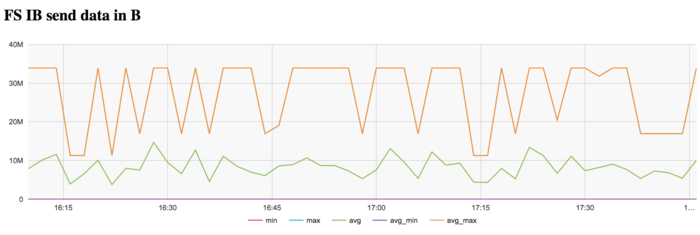
На графике скорости передачи данных по сети Infiniband наблюдается достаточно высокая интенсивность использования сети на кпервом этапе. Это объясняется программной логикой, которая предполагает чтение графа из файла с диска, коммуникации с которым происходят на Ломоносов-2 через выделенную для этих задач сеть Infiniband.
На графике скорости передачи данных в пакетах в секунду наблюдается аналогичная картина очень высокой интенсивности на первом этапе выполнения задачи. Далее сеть почти не используется.
В целом, по данным системного мониторинга работы программы можно сделать вывод о том, что программа работала стабильно интенсивно, однако очень неэффективно использовала память из-за очень большого размера графа.
2.6 Conclusions for different classes of computer architecture
2.7 Existing implementations of the algorithm
- C++: Boost Graph Library (функция
bellman_ford_shortest). - Python: NetworkX (функция
bellman_ford). - Java: JGraphT (класс
BellmanFordShortestPath).