Back substitution

Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (раздел 2.2)

1 Properties and structure of the algorithm

1.1 General description

Backward substitution is a procedure of solving a system of linear algebraic equations [math]Ux = y[/math], where [math]U[/math] is an upper triangular matrix whose diagonal elements are not equal to zero. The matrix [math]U[/math] can be a factor of another matrix [math]A[/math] in its decomposition (or factorization) [math]LU[/math], where [math]L[/math] is a lower triangular matrix. This decomposition can be obtained by many methods (for example, the Gaussian elimination method with or without pivoting, the Gaussian compact scheme, the Cholesky decomposition, etc.). Here we also should mention the [math]QR[/math] decomposition when the matrix [math]A[/math] is represented in the form [math]A=QR[/math], where [math]Q[/math] is an orthogonal matrix and [math]R[/math] is an upper triangular matrix. Since the matrix [math]U[/math] is triangular, a procedure of solving a linear system with the matrix [math]U[/math] is a modification of the general substitution method and can be written using simple formulas.

A similar procedure of solving a linear system with a lower triangular matrix is called the forward substitution (see [1]). Note that the backward substitution discussed here can be considered as a part of the backward Gaussian elimination in the Gaussian elimination method for solving linear systems.

There exists a similar method called the backward substitution with normalization. The scheme of this modification is more complex, since a number of special operations are performed to reduce the effect of round-off errors on the results. This modified method is not discussed here.

1.2 Mathematical description

Input data: an upper triangular matrix [math]U[/math] whose elements are denoted by [math]u_{ij}[/math]); a right-hand vector [math]y[/math] whose components are denoted by [math]y_{i}[/math]).

Output data: the solution vector [math]x[/math] whose components are denoted by [math]x_{i}[/math]).

The backward substitution algorithm can be represented as

[math] \begin{align} x_{n} & = y_{n}/u_{nn} \\ x_{i} & = \left (y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} \right ) / u_{ii}, \quad i \in [1, n - 1]. \end{align} [/math]

There exists a block version of this algorithm; however, here we consider only its “dot” version.

1.3 Computational kernel of the algorithm

The computational kernel of the backward substitution algorithm can be composed of [math]n-1[/math] dot products of subrows of the matrix [math]U[/math] with the computed part of the vector [math]x[/math]:

[math] \sum_{j = i+1}^{n} u_{ij} x_{j} [/math].

Here the dot products can be accumulated in double precision for additional accuracy. These dot products are subtracted from the components of the vector [math]y[/math] and the results are divided by the diagonal elements of the matrix [math]U[/math]. In some implementations, however, this approach is not used. In these implementations, the operation

[math] y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} [/math]

is performed by subtracting the componentwise products as part of dot products from [math]y_{i}[/math] instead of subtracting the entire dot product from [math]y_{i}[/math]. Hence, the operation

[math] y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} [/math]

and the division of the results by the diagonal elements of the matrix should be considered as a computational kernel instead of the dot product operations. Here the accumulation in double precision can also be used.

1.4 Macrostructure of the algorithm

As is stated in description of algorithm’s kernel, the major part of the algorithm consists of computing the ([math]n-1[/math]) sums

[math]y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} [/math]

and dividing the results by the diagonal elements of the matrix. The accumulation in double precision can also be used.

1.5 The implementation scheme of the sequential algorithm

The first stage of this scheme can be represented as

1. [math]x_{n} = y_{n}/u_{nn}[/math].

At the second stage, for all [math]i[/math] form [math]n-1[/math] to [math]1[/math], the following operations should be performed:

2. [math]x_{i} = \left (y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} \right ) / u_{ii}[/math].

Note that the computations of the sums [math]y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j}[/math] are performed in the accumulation mode by subtracting the products [math]u_{ij} x_{j}[/math] from [math]y_{i}[/math] for [math]j[/math] from [math]n[/math] to [math]i + 1[/math] with decreasing [math]j[/math]. Other orders of summation lead to a severe degradation of parallel properties of the algorithm. As an example, we can mention a program fragment given in [2], where the backward substitution is discussed in the form of the backward Gaussian elimination performed with increasing summation index because of the restrictions imposed by old versions of Fortran.

1.6 Sequential complexity of the algorithm

The following number of operations should be performed for the backward substitution in the case of solving a linear system with an upper triangular matrix of order [math]n[/math] using a sequential most fast algorithm:

• [math]n[/math] divisions
• [math]\frac{n^2-n}{2}[/math] additions (subtractions),
• [math]\frac{n^2-n}{2}[/math] multiplications.

The main amount of computational work consists of multiplications and .additions (subtractions)

In the accumulation mode, the multiplication and subtraction operations should be made in double precision (or by using the corresponding function, like the DPROD function in Fortran), which increases the overall computation time of the algorithm.

Thus, the computational complexity of the backward substitution algorithm is equal to [math]O(n^2)[/math].

1.7 Information graph of the algorithm

Let us describe the algorithm’s graph analytically and in the form of a figure.

Граф алгоритма обратной подстановки состоит из двух групп вершин, расположенных в целочисленных узлах двух областей разной размерности. The graph of the backward substitution algorithm]consists of two groups of vertices positioned in the integer-valued nodes of two domains of different dimension.

450px|thumb|left|Fig. 1. Backward substitution.

The first group of vertices belongs to the one-dimensional domain corresponding to the division operation. The only coordinate [math]i[/math] of each vertex changes in the range from [math]n[/math] to [math]1[/math] and takes all the integer values from this range.

The dividend of this division operation:

• for [math]i = n[/math]: the input data element [math]y_{n}[/math];
• for [math]i \lt n[/math]: the result of the operation corresponding to the vertex of the second group with coordinates [math]i[/math], [math]i+1[/math].

The divisor of this division operation is the input data element [math]u_{nn}[/math].

The result of this operation is the output data element [math]x_{i}[/math].

The second group of vertices belongs to the two-dimensional domain corresponding to the operation [math]a-bc[/math].

The coordinates of this domain are as follows:

• the coordinate [math]i[/math] changes in the range from [math]n-1[/math] to [math]1[/math] and takes all the integer values from this range;
• the coordinate [math]j[/math] changes in the range from [math]n[/math] to [math]i+1[/math] and takes all the integer values from this range.

The arguments of this operation:

• [math]a[/math]:
  • for [math]j = n[/math]: the input data element [math]y_{i}[/math];
  • for [math]j \lt n[/math]: the result of the operation corresponding to the vertex of the second group with coordinates [math]i, j+1[/math];
• [math]b[/math]: the input data element [math]u_{ij}[/math];
• [math]c[/math]: the result of the operation corresponding to the vertex of the first group with coordinate [math]j[/math];

The result of this operation is intermediate for the backward substitution algorithm.

The above graph is illustrated in Fig. 1 for [math]n = 5[/math]. In this figure, the vertices of the first group are highlighted in yellow and are marked by the division sign; the vertices of the second group are highlighted in green and are marked by the letter f. The graph shows the input data transfer from the vector [math]y[/math], whereas the transfer of the matrix elements [math]u_{ij}[/math] to the vertices is not shown.

1.8 Parallelization resources of the algorithm

In order to implement the backward substitution algorithm for a linear system with an upper triangular matrix of order [math]n[/math], a parallel version of this algorithm should perform the following layers of operations:

• [math]n[/math] layers of divisions (one division on each of the layers),
• [math]n - 1[/math] layers of multiplications and [math]n - 1[/math] layers of addition/subtraction (on each of the layers, the number of these operations is linear and varies from [math]1[/math] to [math]n-1[/math].

Contrary to a sequential version, in a parallel version the division operations require a significant part of overall computational time. The existence of isolated divisions on some layers of the parallel form may cause other difficulties for particular parallel computing architectures. In the case of programmable logic devices (PLD), for example, the operations of multiplication and addition/subtraction can be conveyorized, which is efficient in resource saving for programmable boards, whereas the isolated division operations acquire resources of such boards and force them to be out of action for a significant period of time.

In addition, we should mention the fact that the accumulation mode requires multiplications and subtraction in double precision. In a parallel version, this means that almost all intermediate computations should be performed with data given in their double precision format. Contrary to a sequential version, hence, the amount of the necessary memory increases to some extent.

Thus, the backward substitution algorithm belongs to the class of algorithms of linear complexity in the sense of the height of its parallel form; its complexity is also linear in the sense of the width of its parallel form.

1.9 Описание входных и выходных данных

Входные данные: верхняя треугольная матрица [math]U[/math] (элементы [math]u_{ij}[/math]), вектор правой части [math]y[/math] (элементы [math]y_{i}[/math]).

Объём входных данных: :[math]\frac{n (n + 3)}{2}[/math] (в силу треугольности достаточно хранить только ненулевые элементы матрицы [math]U[/math]).

Выходные данные: вектор решения [math]x[/math] (элементы [math]x_{i}[/math]).

Объём выходных данных: :[math]n~.[/math]

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение квадратической к линейной).

При этом вычислительная мощность алгоритма обратной подстановки, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь константа.

При этом алгоритм обратной подстановки полностью детерминирован. Использование другого порядка выполнения ассоциативных операций в данной версии нами не рассматривается, поскольку в корне меняет структуру алгоритма и меняет сложность с параллельной на квадратичную.

Наличие линейного количества ярусов ЯПФ, состоящих из одного-единственного деления, потенциально замедляющее параллельные реализации алгоритма, является его характерным "узким местом", особенно в сравнении со схожей по решаемой математической задаче прямой подстановке, где диагональные элементы единичны. В связи с этим для решения СЛАУ предпочтительны такие разложения, содержащие треугольные матрицы, где в треугольных матрицах диагональные элементы единичны. В тех же случаях, когда получаются неособенные треугольные матрицы, их желательно предварительно, до решения СЛАУ с ними, преобразовать в произведение диагональной и треугольной с единичными диагональными элементами.

У алгоритма обратной подстановки существует несколько блочных вариантов. Граф некоторых из них совпадает с графом точечного варианта, различия связаны в основном с порядком прохождения основных циклов алгоритма, а именно - с их развёртыванием и перестановкой. Эти приёмы могут помочь в оптимизации обменов на конкретных вычислительных системах.

2 Программная реализация

2.1 Особенности реализации последовательного алгоритма

В простейшем варианте метод обратной подстановки на Фортране можно записать так:

        X(N) = Y(N) / U (N, N)
	DO  I = N-1, 1, -1
		S = Y(I)
		DO  J = N, I+1, -1
			S = S - DPROD(U(I,J), X(J))
		END DO
		X(I) = S / U(I,I)		
	END DO

При этом для реализации режима накопления переменная [math]S[/math] должна быть двойной точности.

2.2 Описание локальности данных и вычислений

2.2.1 Описание локальности реализации алгоритма

2.2.1.1 Описание структуры обращений в память и качественная оценка локальности

Рисунок 12.1. Обратный ход метода Гаусса решения СЛАУ. Общий профиль обращений в память

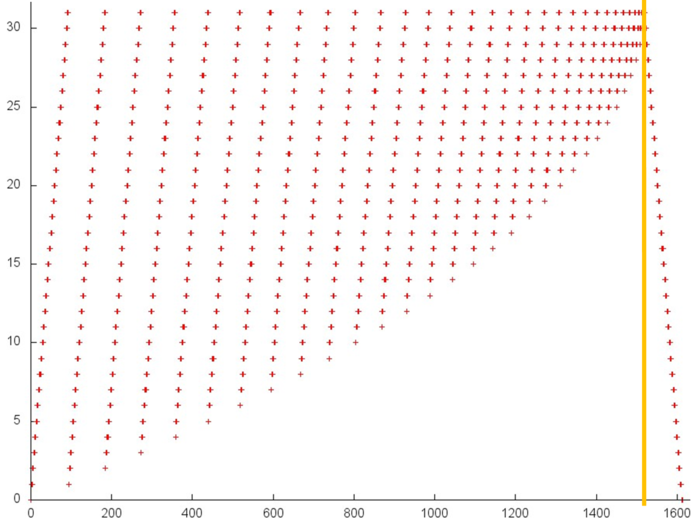
На рисунке 12.1 представлен профиль обращений в память для обратного хода метода Гаусса решения СЛАУ. Хорошо видно, что профиль состоит из двух этапов, идущих друг за другом (граница между ними выделена оранжевой линией). Это соответствует двум циклам, из которых собственно состоит исходный код обратного хода метода Гаусса. Из самого рисунка это заметить достаточно сложно, но анализ исходного кода показывает, что профиль образуется из обращений к 4 массивам. Три из них выделены на рис. 12.1 зеленым; к четвертому относятся все остальные обращения. Сразу отметим, что в данном профиле общее число обращений всего в несколько раз больше числа задействованных элементов массивов (4500 против 1000), а в таких условиях сложно добиться высокой локальности.

Чтобы выяснить это, перейдем к подробному рассмотрению каждого из массивов в отдельности.

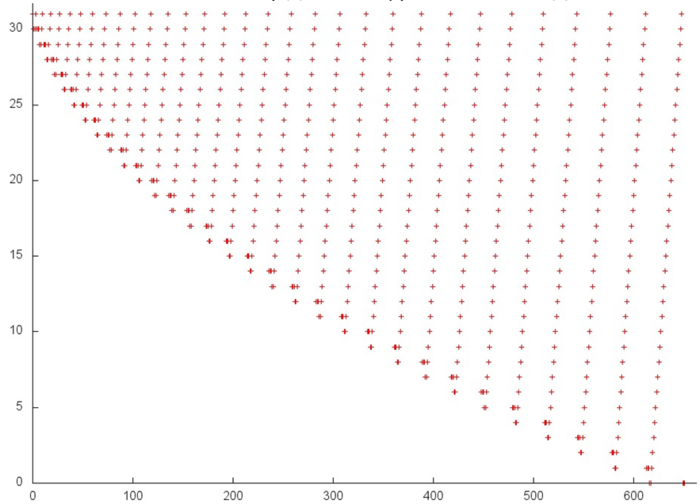
На рис. 12.2 представлен фрагмент 1. Оранжевой линей также проведено разделение 2 этапов. Видно, что второй этап устроен очень просто и представляет собой последовательный перебор в обратном порядке. Первый этап имеет итерационный характер, причем на каждой итерации отбрасывается элемент массива с наименьшим номером. Подобный профиль характеризуется высокой пространственной локальностью, поскольку элементы перебираются подряд; достаточно высокой временной локальностью, поскольку на каждой итерации происходит повторное обращение к тем же элементам.

Рисунок 12.2. Фрагмент 1 (профиль обращений к первому массиву)

На рис. 12.3 представлен фрагмент 2, показывающий обращения ко второму массиву. Сразу заметим, что данный фрагмент еще меньше предыдущего – здесь задействовано всего 600 обращений в память. По сути, данный фрагмент является аналогичным этапу 1 фрагмент 1, с единственной разницей – здесь итерации расположены в обратном порядке. Однако это изменение не оказывает особого влияния ни на пространственную, ни не временную локальность, поэтому данный фрагмент обладает теми же свойствами.

Рисунок 12.3. Фрагмент 2 (профиль обращений ко второму массиву)

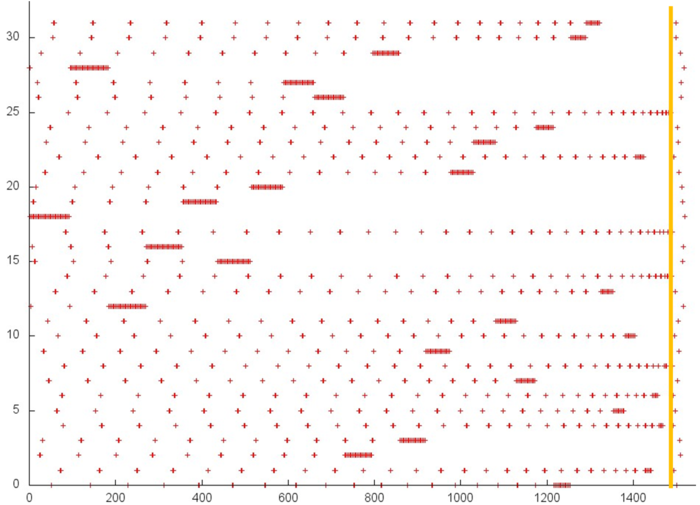
Далее рассмотрим фрагмент 3 (рис. 12.4). Здесь также оранжевой линией проведено разделение между двумя этапами, и также на второй этап приходится совсем немного обращений. Обращения на первом этапе образуют аналог случайного доступа, достаточно часто встречающийся, например, в случае косвенной адресации. При этом в некоторый момент к определенному элементу происходит достаточно много обращений подряд, после чего этот элемент более не используется. Такой профиль обычно характеризуется низкой пространственной и временной локальностью, что, однако, в данном случае в достаточной степени нивелируется малым числом задействованных элементов.

Рисунок 12.4. Фрагмент 3 (профиль обращений к третьему массиву)

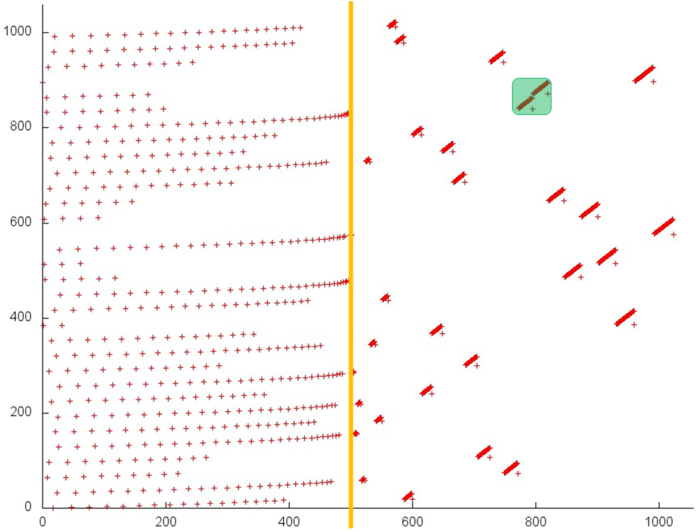
Далее перейдем к фрагменту, занимающему основную часть рис. 12.1. Данный профиль отображен на рис. 12.5. В первую очередь стоит отметить особенность данного профиля – здесь задействовано более 1000 элементов, в то время как в остальных профилям – порядка 30. При этом число обращений даже меньше, чем обращений к первому или третьему массиву.

Отметим также, что здесь большая часть обращений сосредоточена на втором этапе. Первый же этап является подобием первого этапа предыдущего массива (рис. 12.4) , за тем лишь исключением, что в данном профиле отсутствуют множественные обращения подряд к одному элементу перед тем, как элемент перестанет использоваться. С учетом того, что первый этап состоит всего из порядка 500 обращений, достаточно равномерно распределенных на отрезке в 1000 элементов, это говорит об очень низкой как пространственной, так и временной локальности.

Другой характер обращений можно наблюдать на втором этапе. Видно, что он обладает более высокой пространственной локальностью, так как обращения явно сгруппированы в кластеры, при этом кластеры обладают подобным строением. Однако структура самого кластера видно плохо, поэтому требуется дальнейшее приближение.

Рисунок 12.5. Фрагмент 4 (профиль обращений к четвертому массиву)

На рис. 12.6 показаны два кластера, выделенные на рис. 12.5 зеленым цветом. Такой масштаб позволяет сразу увидеть, что каждый кластер представляет собой последовательный перебор с небольшим шагом определенного набора элементов массива.

Следовательно, можно говорить о том, что второй этап фрагмента 4 обладает достаточно высокой пространственной локальностью (поскольку каждый кластер содержит последовательный перебор), но низкой временной локальностью (повторные обращения практически отсутствуют).

Рисунок 12.6. Два кластера из фрагмента 4

В целом по всему профилю можно сделать следующий вывод: первый три рассмотренных массива (особенно №1 и №2) обладают достаточно высокой локальностью, однако достаточно низкая пространственная и очень низкая временная локальность последнего массива в значительной степени снижают общую локальность всей программы.

2.2.1.2 Количественная оценка локальности

Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel2). Условия запуска описаны здесь.

Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

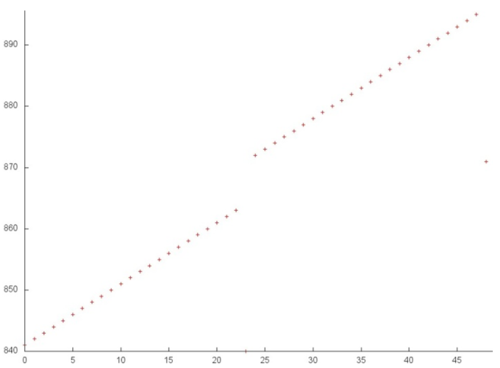
На рисунке 12.7 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что, в соответствии с высказанным в предыдущем разделе предположением о негативном влиянии одного из массивов, данная программа показывает достаточно низкую производительность, заметно ниже, чем у прямого хода метода Гаусса.

File:Gauss back daps ru.PNG

Рисунок 12.7. Сравнение значений оценки daps

Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.

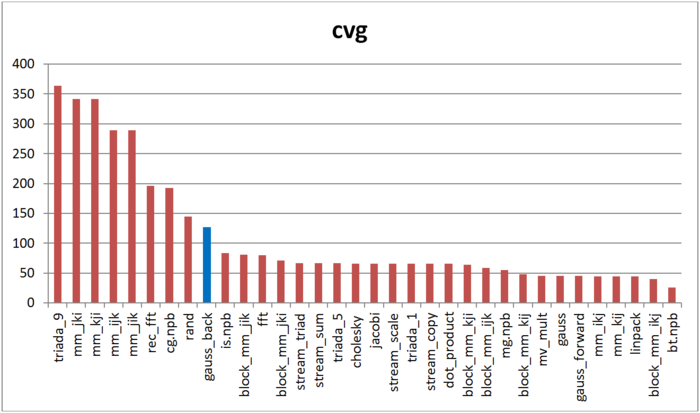
На рисунке 12.8 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, профиль обращений обладает низкой локальностью, лишь немногим лучше профиля программы со случайным доступом в память. Это повторяет выводы, сделанные на основе оценки daps.

Рисунок 12.8. Сравнение значений оценки cvg

2.3 Возможные способы и особенности реализации параллельного алгоритма

Вариантов параллельной реализации алгоритма не так уж и много, если не использовать то, что оба главных цикла можно развернуть, перейдя, таким образом, к блочной версии. Версии без развёртывания циклов возможны как с полностью параллельными циклами по I:

        DO  PARALLEL I = 1, N
           X(I) = Y(I)
        END DO
        DO J = N, 1, -1
           X(J) = X(J) / U(J,J)
           DO PARALLEL I = 1, J-1
              X(I) = X(I) - U(I,J)*X(J)
           END DO
        END DO

так и с использованием "скошенного параллелизма" в главном гнезде циклов.

2.6 Выводы для классов архитектур

Если исходить из структуры алгоритма, то при реализации на суперкомпьютерах следует выполнить две вещи. Во-первых, для минимизации обменов между узлами следует избрать блочный вариант, в котором или все элементы матрицы доступны на всех узлах, или заранее распределены по узлам. В таком случае количество передаваемых между узлами данных будет невелико по сравнению с количеством арифметических операций. Но при такой организации работы получится, что наибольшие временные затраты будут связаны с неоптимальностью обработки отдельных блоков. Поэтому, видимо, следует сначала оптимизировать не блочный алгоритм в целом, а подпрограммы, используемые на отдельных процессорах: точечный метод обратной подстановки, перемножения матриц и др. подпрограммы. Ниже содержится информация о возможном направлении такой оптимизации.

2.7 Существующие реализации алгоритма

Вещественный вариант обратной подстановки реализован как в основных библиотеках программ отечественных организаций, так и в западных пакетах LINPACK, LAPACK, SCALAPACK и др. При этом в отечественных реализациях, как правило, выполнены стандартные требования к методу с точки зрения ошибок округления, то есть, реализован режим накопления, и обычно нет лишних операций. Реализация точечного метода Холецкого в современных западных пакетах обычно происходит из одной и той же реализации метода в LINPACK, а та использует пакет BLAS.

Для большинства пакетов существует блочный вариант обратной подстановки, в том числе и тот, граф которого топологически тождествен графу точечного варианта. Из-за того, что количество читаемых данных примерно равно количеству операций, блочность может дать некоторое ускорение работы благодаря лучшему использованию кэшей процессоров. Именно в направлении оптимизации кэширования и следует сосредоточить основные усилия при оптимизации работы программы.

3 References

1. V.V. Voevodin, Yu.A. Kuznetsov. Matrices and computations. Moscow: Nauka, 1984 (in Russian).
2. G. Forsythe and C. Moler. Computer Solution of Linear Algebraic Systems. Englewood Cliffs: Prentice Hall, 1967 (Russian translation: Дж.Форсайт, К.Моллер. Численное решение систем линейных алгебраических уравнений.М.: Мир, 1969).