Boruvka's, scalability
Primary author of this description: I.V.Afanasyev.
Contents
1 Links
The experiments were conducted with Borůvka's algorithm implemented for CPU.
2 Locality of data and computations
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
2.1.2 Quantitative estimation of locality
3 Scalability of the algorithm and its implementations
3.1 Scalability of the algorithm
The possibility of processing fragments independently of each other implies a good scalability of the algorithm. The restraining factors are:
- memory bandwidth while reading information on the graph;
- rivalry of data streams while performing atomic operations with memory;
- barrier synchronization after each half step of the algorithm.
3.2 Scalability of of the algorithm implementation
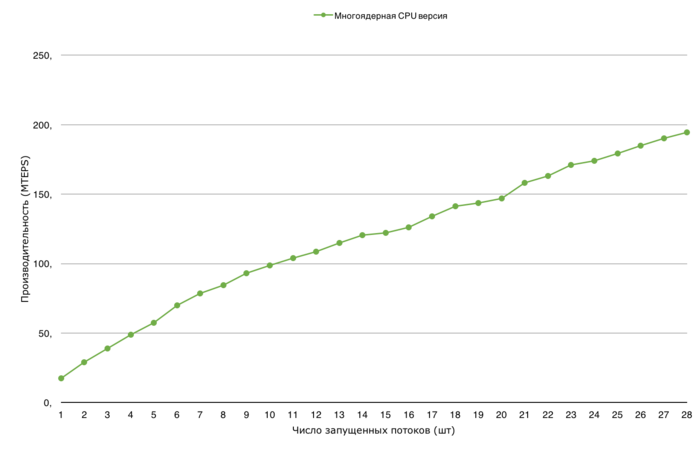
Let us study scalability for the parallel implementation of Borůvka's algorithm in accordance with Scalability methodology. This study was conducted using the Lomonosov-2 supercomputer of the Moscow University Supercomputing Center.
Variable parameters for the start-up of the algorithm implementation and the limits of parameter variations:
- number of processors [1 : 28] with the step 1;
- graph size [2^20 : 2^27].
We perform separate analyses of strong scalability and scaling-out of the implementation of Borůvka's algorithm.
The performance is defined as TEPS (an abbreviation for Traversed Edges Per Second), that is, the number of graph arcs processed by the algorithm in a second. Using this characteristic, one can compare the performance for graphs of different sizes and estimate how the performance gets worse when the graph size increases.
4 Dynamic characteristics and efficiency of the algorithm implementation
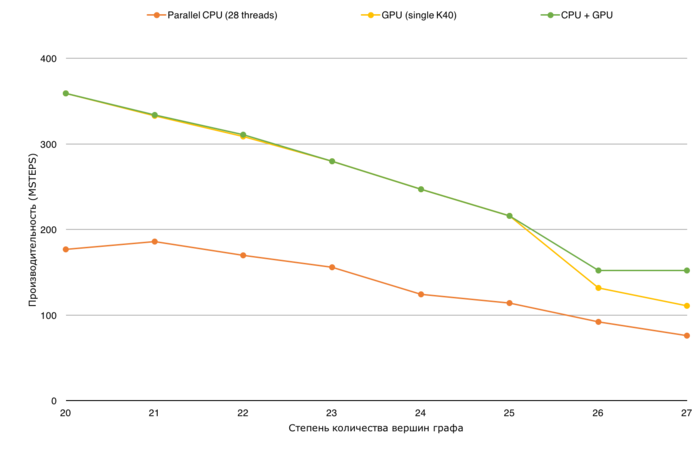
All the results were obtained with the «Lomonosov-2» supercomputer. We used Intel Xeon E5-2697v3 processors. The problem was solved for a large graph (of size 2^27) on a single node. Only one iteration was performed. The figures below illustrate the efficiency of this implementation.
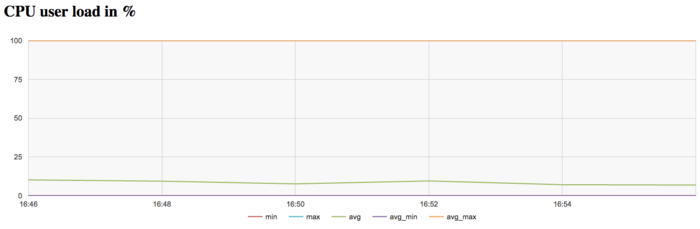
The graph of CPU loading shows that the processor is idle almost all the time: the average level of loading is about 10 percent. This is an ordinary result for programs launched with the use of only one core.
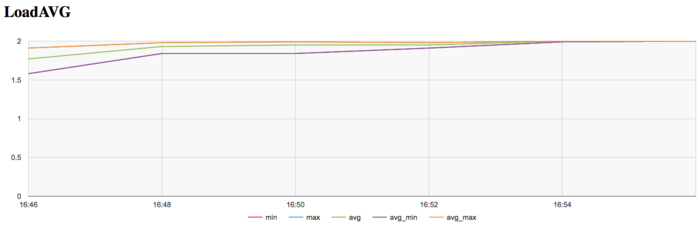
The graph of the number of processes expecting the beginning of the calculation stage (Loadavg) shows that the value of this parameter in the course of the program execution is always close to 2. This indicates that the hardware resources are all the time loaded by at most two processes. Such a small number points to a not very reasonable use of resources.
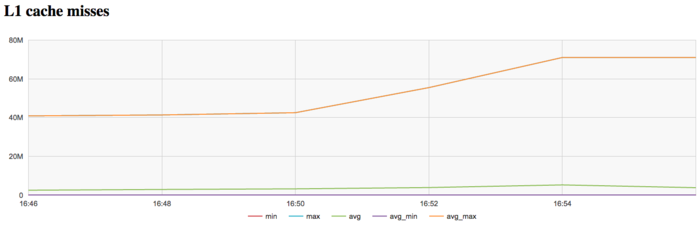
The graph of L1 cache misses shows that the number of misses is very large (on the level of 40 millions per second). It is interesting that this number increases to the level of 70 millions per second to the end of iteration.
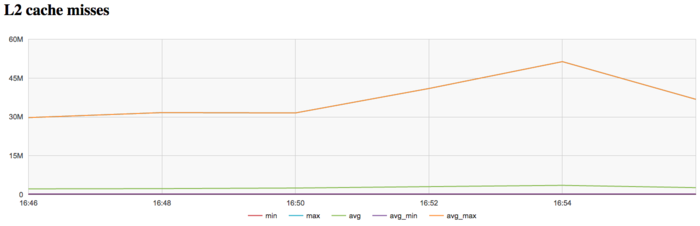
The graph of L2 cache misses shows that the number of such misses is also very large (on the level of 30 millions per second). This number increases to the end of iteration (to the level of 50 millions per second). Such an increase is more evident here than in figure 13.
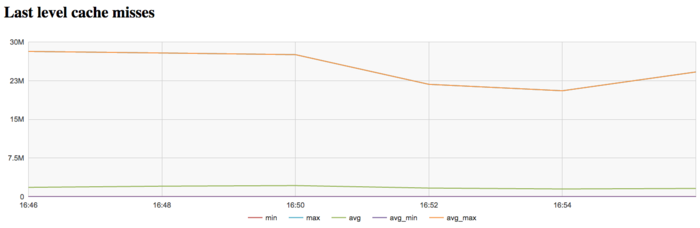
The graph of L3 cache misses shows that the number of these misses is again large; it is about 30 millions per second. This indicates that the problem fits very badly into cache memory, and the program is compelled to work all the time with RAM, which is explained by the very large size of the input graph.
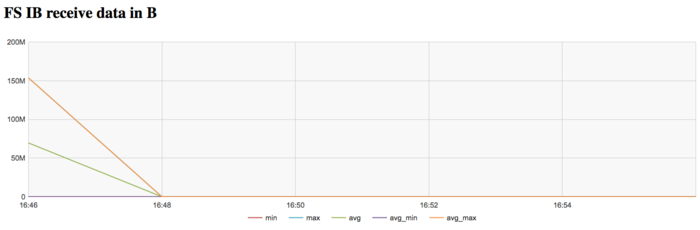
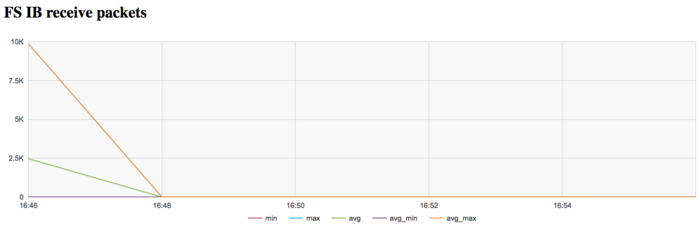
The graph of the data rate through Infiniband network shows a fairly high intensity of using this network at the first stage. This is explained by the program logic, which assumes the reading of the graph from a disc file. On Lomonosov-2, communications with this disc are performed through a dedicated Infiniband network.
The graph of the data rate measured in packets per second demonstrates a similar picture of very high intensity at the first stage of executing the problem. Later on, the network is almost not used.
On the whole, the data of system monitoring make it possible to conclude that the program worked with a stable intensity. However, it used the memory very inefficiently due to the extremely large size of the graph.