Boruvka's, locality
Primary author of this description: I.V.Afanasyev.
Contents
1 Links
The basic fragment of the implementation used for obtaining quantitative estimates is given here (function Kernel).
2 Locality of data and computations
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
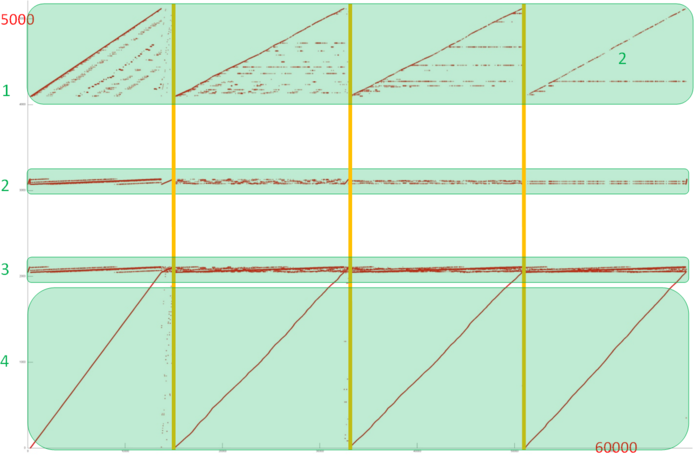
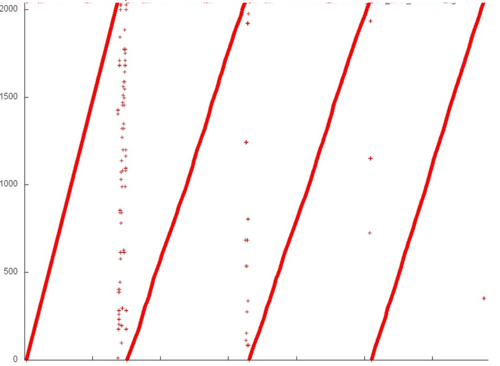
Fig.1 shows the memory access profile for an implementation of Borůvka's algorithm. Similarly to most of the graph algorithms, this one has an irregular structure. Note right away that, for implementations of such algorithms, the locality depends in many ways on the structure of the input graph and may change significantly. Here, we consider only one of the possible variants.
One can see that the overall profile consists of four rather similar stages (which are separated by vertical lines in fig.1). Since the structure of this profile is irregular, it is better to examine all the stages.
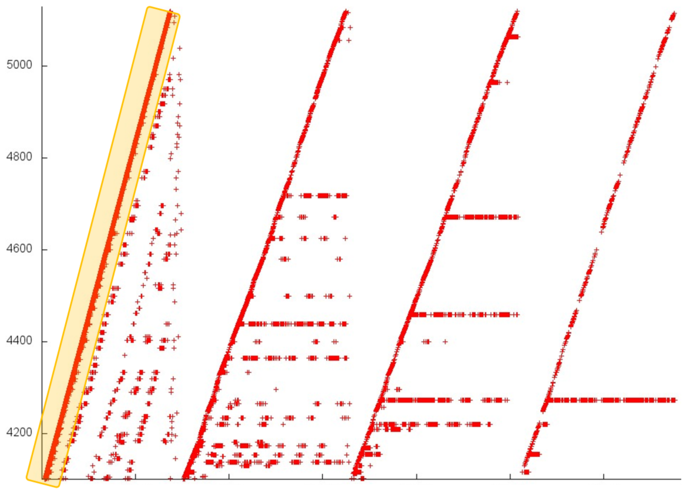
We begin with the analysis of the upper part of the profile (fragment 1 in fig.1). It is shown in fig.2. At each stage, the major portion of memory accesses are successive searches through the elements of this fragment (set out in yellow in fig.2). Other accesses are structured variously at different stages. At the first stage, the accesses are scattered rather far from each other, which implies a low locality (both spatial and temporal). By contrast, at the last stage, almost all accesses (off the successive search) are performed to one and the same element, which, naturally, ensures a very high locality. Such a structure of the entire fragment most likely results in moderate values of both the spatial and temporal locality.
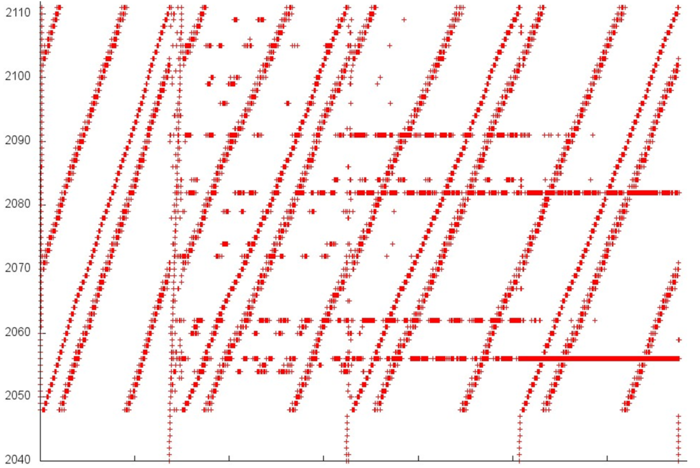
Now, we turn to the analysis of fragment 2 (fig.3). Here, one can see that all the four stages differ widely in structure. Similarly to the situation with fragment 1, each next stage has a higher locality, but, here, this feature is more evident. Note that this fragment involves only about 60 elements, whereas these elements are accessed fairly often. Consequently, the locality in this case is high.
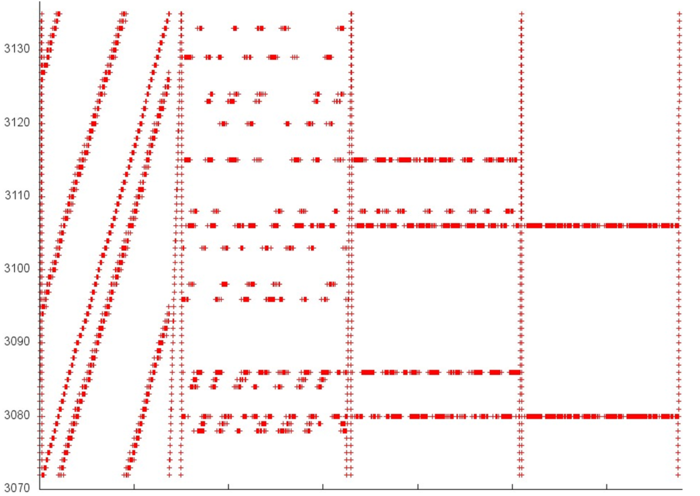
On the whole, a similar picture is observed in fragment 3. In fig.4, one can see four stages with a resembling structure, and, again, about 60 elements are involved. This allows us to assert the high locality of this fragment.
A separate examination of fragment 4 (see fig.5) allows one to see that the locality is determined here by four successive searches through all the elements of this fragment. These searches have the conventional structure: step through memory equal to 1, and a sole access to each element. A small distortion of the searches is caused by an irregular activity in other fragments, which results in the contortion of the visual representation of the profile. Such a set of accesses has a high spatial locality but a low temporal one.
Thus, fragments 2 and 4 are characterized by a high locality, while the other two fragments have a modest locality. Since the majority of accesses are exactly those to fragments 2 and 3, it seems likely that the overall locality is rather high.
2.1.2 Quantitative estimation of locality
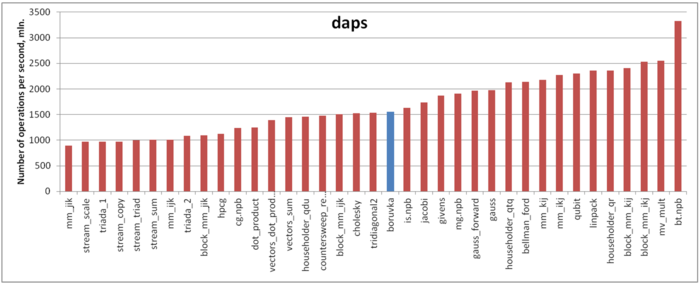
Our estimate is based on daps, which assesses the number of memory accesses (reads and writes) per second. Similarly to flops, daps is used to evaluate memory access performance rather than locality. Yet, it is a good source of information, particularly for comparison with the results provided by the estimate cvg.
Fig.6 shows daps values for implementations of popular algorithms, sorted in ascending order (the higher the daps, the better the performance in general). One can see that the memory access performance of this implementation is not bad. In particular, its daps value is, for instance, comparable with that for the implementation of the Cholesky method. However, it is considerably smaller than those for the most productive implementations (for example, one of the Linpack benchmark). On the whole, this is not surprising in the case of graph algorithms with their tradition of the inefficient use of memory.