Cholesky decomposition, scalability
Jump to navigation
Jump to search
Primary author of this description: Alexey Teplov (Section 3).
Contents
1 Links
The C language implementation of the parallel Cholesky decomposition.
2 Locality of data and computations
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
2.1.2 Quantitative estimation of locality
3 Scalability of the algorithm and its implementations
3.1 Scalability of the algorithm
3.2 Scalability of of the algorithm implementation
The research was performed with the use of the Lomonosov supercomputer[1] installed at the Research Computing Center of Moscow State University.
Let us perform a scalability analysis of a particular implementation of the Cholesky algorithm according to the scalability methodology.
- the number of processors [4 : 256] with the step equal to 4;
- the orders of matrices [1024 : 5120].
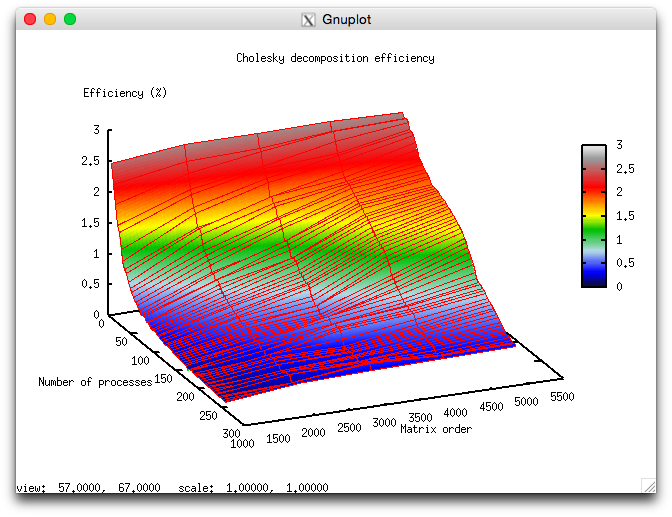
- minimum 0,11%;
- maximum 2,65%.
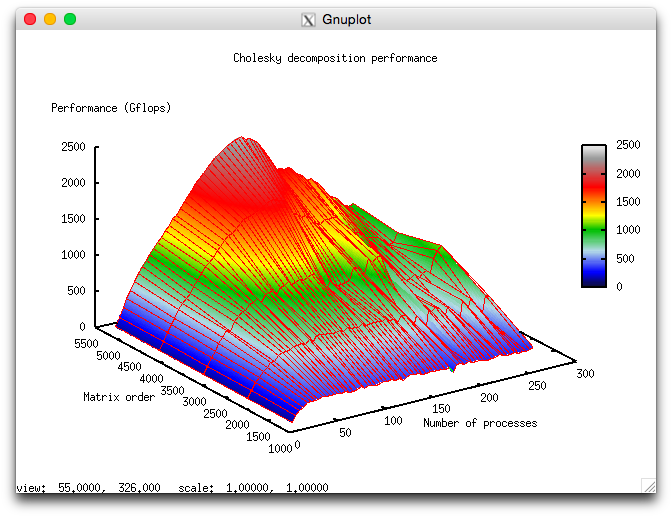
Figures 1 and 2 illustrate the performance and efficiency of the chosen parallel implementation of the Cholesky algorithm, depending on the startup parameters.
Below we discuss some estimations of scalability for the chosen implementation of the Cholesky decomposition.
- In accordance with the number of processes: -0,000593. If the number of processes increases, then the efficiency is reduced for the chosen range of the startup parameters, but this efficiency reduction is not very fast. Such a small reduction in performance variation can be explained by the fact that the general performance efficiency is very low (its maximum is equal to 2,65%); as a result, the algorithm’s efficiency is reduced down to one-tenth percent. Hence, this efficiency reduction is not intensive for the most part of the startup parameter range and becomes not fast with an increase of computational complexity. The efficiency reduction can also be explained by a fast increase in the excessive consumption of computational resources due to the management of parallel execution. When the computational complexity increases, the efficiency reduction is also fast if the number of processes is large. This confirms our assumption that the excessive consumption of computational resources prevail significantly over the computational cost.
- In accordance with the matrix order: 0,06017. When the matrix order increases, the performance efficiency also increases. This increase is faster if the number of processes used for solving the problem increases. This fact confirms our assumption that the matrix order essentially influences the performance efficiency. Our estimations shows that this efficiency significantly increases with an increase of the matrix order for the above range of the startup parameters. Taking into account the difference between the maximum and minimum efficiency (about 2,5%), we can conclude that such a growth of the efficiency is observed for the most part of the startup parameter range.
- In accordance with the two directions of parameter variation: 0,000403. If the computational complexity and the number of processes become larger, then the performance efficiency increases slowly with small jumps.
4 Dynamic characteristics and efficiency of the algorithm implementation
5 Run results
6 References
- ↑ Voevodin Vl.V., Zhumatii S.A., Sobolev S.I., Antonov A.S., Bryzgalov P.A., Nikitenko D.A., Stefanov K.S., Voevodin Vad.V. The Lomonosov supercomputer in practice. Otkrytye Sistemy (2012) No. 7, 36-39.