Dot product, scalability

Primary author of this description: A.M.Teplov (Section 3).

1 Links

Studied parallel implementation in C.

3 Scalability of the algorithm and its implementations

3.2 Scalability of of the algorithm implementation

Figure 1. Parallel implementation of the scalar product of vectors, maximum performance.

Figure 2. Parallel implementation of the scalar product of vectors, maximum efficiency.

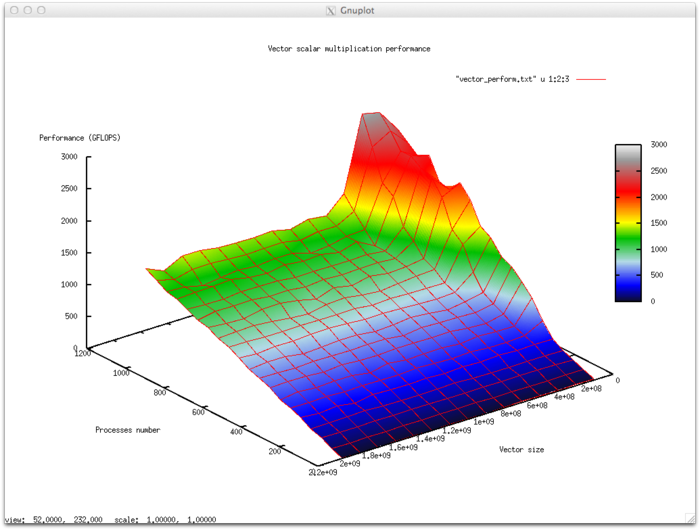
Variable parameters for implementation algorithm execution and the limits of parameter variations:

• number of processors [4 : 1024]
• vector size [134217728 : 2013265920]

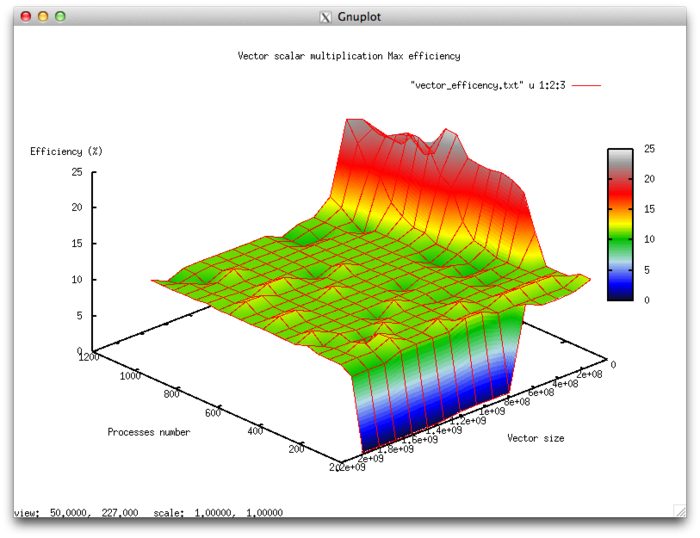
Efficiency of algorithm implementation execution

• Minimum efficiency: 9.54 %
• Maximum efficiency: 24.52%

Scalability assessment

• By the number of processes: 0.00414 – as the number of processes increases within the given range of execution parameters, so does the efficiency. But overall, the increase is not very intensive. The increase in efficiency at the given range of variable parameters for the parallel program is explained by the fact that as the number of processors increases, at some point data begins to fit better into cache memory, thanks to decomposition. This is confirmed by the phenomenon manifesting itself with a shift over the number of processes, and consistently with an increase in the computing complexity of the task.
• By size of the task: -0.01385 – as the task size increases, its efficiency generally falls within the given range of execution parameters. This is explained by the fact that the data fits well in cache memory for smaller tasks, resulting in high application efficiency. As the task size increases, efficiency drops as the cache memory limits are exceeded.
• By two dimensions: -0.000169 – as both computing complexity and the number of processes increase through the given range of execution parameters, efficiency is reduced, though at a very small rate. Combined with a difference of almost 15% between the maximum and minimum efficiency, this shows that there are areas on the surface with very small efficiency changes, but they are small in size. On the rest of the surface, efficiency changes are insignificant, staying around the same level.