The serial-parallel summation method, locality

Primary author of this description: Vad.V.Voevodin (Section 3).

1 Links

The main implementation fragment, which is used in all quantitative assessments, is shown here [1](KernelOpSeqpar function).

2 Locality of data and computations

2.1 Locality of implementation

2.1.1 Structure of memory access and a qualitative estimation of locality

Figure 1. Summing the elements of an array. Overall memory address profile

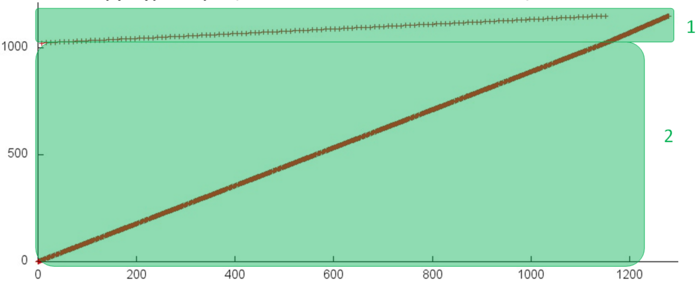
Fig.1 shows the memory address profile for summing the elements of an array. This profile consists of accesses to two arrays; the fragments for individual arrays are highlighted in green in Fig.1. Since we discuss the serial implementation of the serial-parallel summation method, the profile structure is practically independent of the number of branches chosen – only the number of elements involved in fragment 1 will be different.

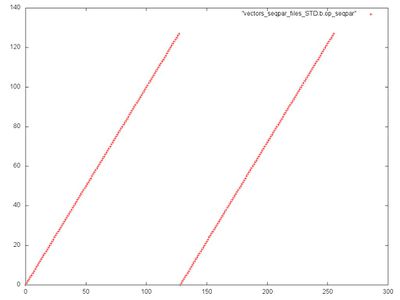
Fragment 2 has a very simple structure; it represents a serial search of all array elements. Fragment 1 consists of two identical serial searches of all array elements. This is clearly seen in Fig.2, which gives a separate picture of this fragment.

Figure 2. Fragment 1 (first array address profile)

This fragment is characterized by high spatial locality and low temporal locality since practically no repeated calls to elements are done.

2.1.2 Quantitative estimation of locality

Launch conditions are described here [2].

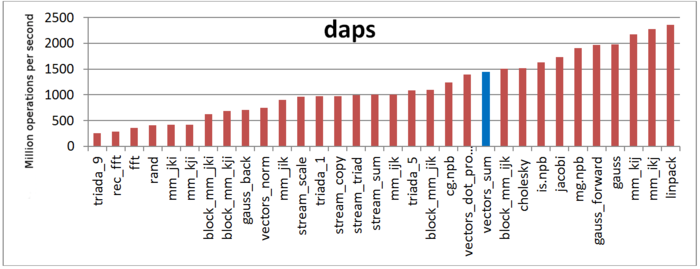
The first estimate is based on daps, which assesses the number of memory access operations (reads and writes) per second. Similar to flops, daps is used to evaluate memory access performance rather than locality. Yet, it is a good source of information, particularly for comparison with the results provided by the next estimate cvg.

Fig.3 shows daps values for implementations of popular algorithms, sorted in ascending order (the higher the daps, the better the performance in general). It is seen that these values are sufficiently high, and they are close to those for the serial-parallel dot product of two vectors. This is not surprising because both procedures execute operations of the same type.

Figure 3. Comparison of daps values

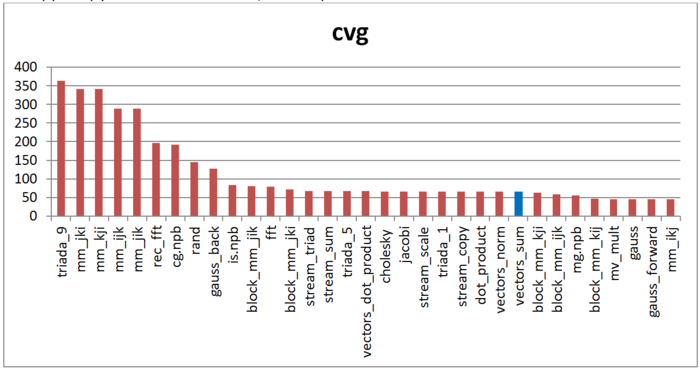
The second tool – cvg – is intended for obtaining a more machine-independent locality assessment. It determines how often a program needs to pull data to cache memory. Accordingly, the smaller the cvg value, the less frequently data need to be called to cache, and the better the locality.

Fig.4 shows the cvg values for the same set of implementations sorted in descending order (the smaller the cvg, the higher the locality in general). One can see that, according to this assessment, the locality profile is sufficiently high, which correlates with the daps values.

Figure 4. Comparison of cvg values