The serial-parallel summation method, scalability
Revision as of 15:08, 8 July 2022 by ASA (talk | contribs) (Created page with "{{level-i}} Primary author of this description: A.M.Teplov (раздел Section 3)....")
Primary author of this description: A.M.Teplov (раздел Section 3).
Contents
1 Links
The algorithm implemented in C.
2 Locality of data and computations
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
2.1.2 Quantitative estimation of locality
3 Scalability of the algorithm and its implementations
3.1 Scalability of the algorithm
3.2 Scalability of of the algorithm implementation
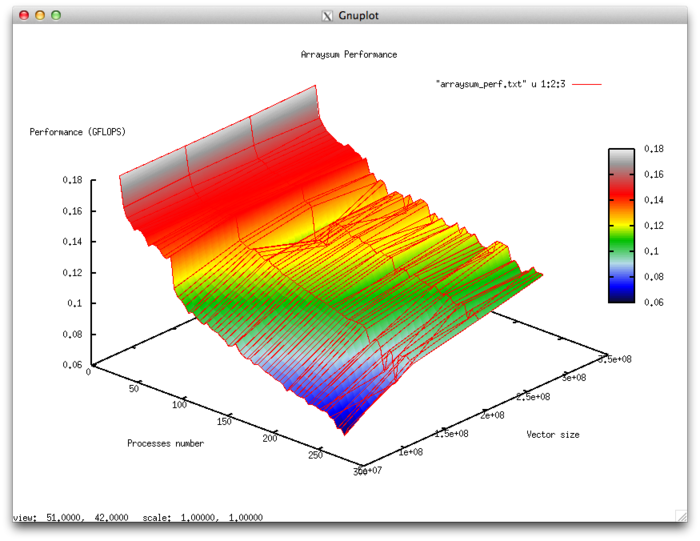
Variable parameters for the launch of the algorithm implementation and the limits of parameter variations:
- number of processors [2 : 256]
- vector size [80000000:320000000]
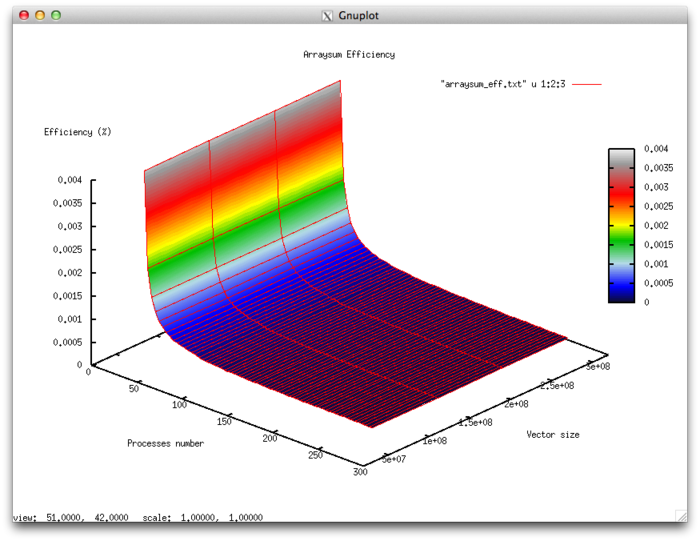
Efficiency of the algorithm implementation
- Minimum efficiency 0,00004%
- Maximum efficiency 0,0037%
Scalability assessment
- By the number of processes: -9.432e-07 – as the number of processes increases, the efficiency (within the given range for the launch parameters) is reduced. But overall, the reduction is not very intensive. This is explained by the fact that an increase in the number of processors entails a strong increase of the costs for the organization of the doubling scheme for summation. However, the overall efficiency is only fractions of percentage; consequently, the intensity is only strong when, instead of the processes within a single physical node, we consider the use of a communication network. For the other values of the launch parameters, the efficiency is close to zero because an extremely small fraction of the overall calculation falls on each single process. Most of the productive time is taken by the organization of the processes .
- By the size of a problem: 1.881e-06 – as the size of the problem increases, the overall efficiency (within the region under discussion) increases very slightly. This is explained by an overall increase in the computational complexity of the problem due to increasing dimensionality. However, the computational complexity of the algorithm, equal to [math](N-1)[/math], does not allow to significantly increase the portion of time spent on calculations.
- Along two directions: -1.423e-07 – Suppose that both the computational complexity and the number of processes increase over the entire region under discussion. Then the efficiency decreases; however, the reduction in efficiency is insignificant. For the parameters under discussion, the difference between the maximum and minimum efficiency is negligible. This says that there are regions on this surface with a very intensive change of efficiency for 2 to 16 processes; however, the area of these regions is very small. On the rest of the surface, the changes in efficiency are minor and have about the same level.