Linpack, HPL
Revision as of 16:11, 12 July 2022 by ASA (talk | contribs) (Created page with "{{level-i}} Primary author of this description: A.M.Teplov (раздел Section 3)....")
Primary author of this description: A.M.Teplov (раздел Section 3).
Contents
1 Links
Study of a test implementation.
2 Locality of data and computations
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
2.1.2 Quantitative estimation of locality
3 Scalability of the algorithm and its implementations
3.1 Scalability of the algorithm
3.2 Scalability of of the algorithm implementation
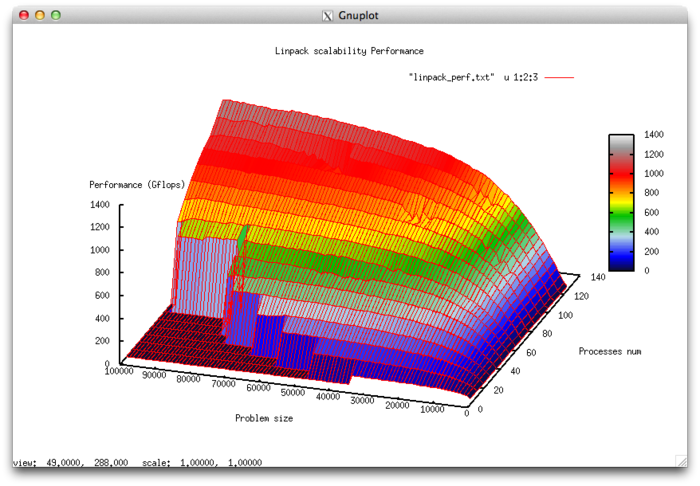
Let us study scalability for the implementation of the HPL Linpack test in accordance with Scalability methodology. This study was conducted using the Lomonosov supercomputer of the Moscow University Supercomputing Center.
Variable parameters for the launch of the algorithm implementation and the limits of parameter variations:
- number of processors [8 : 128] with the step 8;
- matrix size [1000 : 100000] with the step 1000.
The experiments resulted in the following range of implementation efficiency:
- minimum implementation efficiency 0.039%;
- maximum implementation efficiency 86,7%.
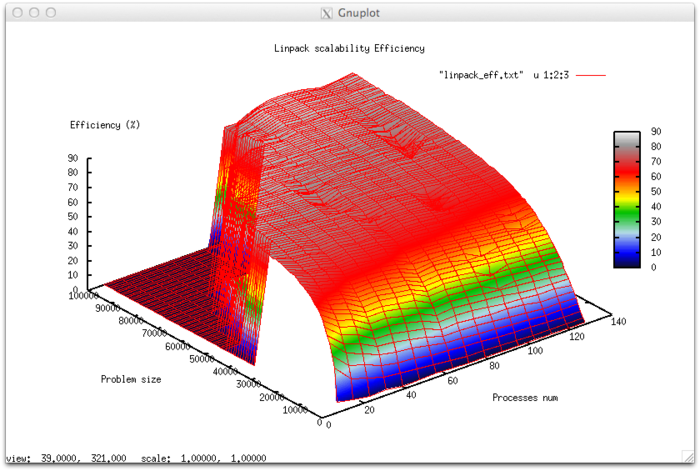
The following figures show the graphs of the performance and efficiency for the HPL test as functions of the variable launch parameters.
Let us assess the scalability of the Linpack test:
- By the number of processes: -0.061256. As the number of processes increases, the efficiency (within the given range for the launch parameters) is reduced . But, overall, the reduction is not very rapid. The small intensity of the change is explained by the fact that, for large size problems, the overall efficiency is high. However, efficiency uniformly decreases with a rise in the number of processes. Another reason is that a rise in the computational complexity makes the reduction of efficiency not so fast. For the range covered, the decrease in the efficiency of the parallel program is explained by the growth of expenses on the organization of parallel execution. The reduction in efficiency is equally fast when the computational complexity increases and the number of processes is large. This confirms the surmise that the overhead expenses begin to strongly prevail over computations.
- By the size of a problem: 0.010134. Efficiency increases with the growth in the size of a problem. The increase is the faster the more processes are executed. This confirms the surmise that the problem size strongly affects the efficiency of execution. The estimate indicates that, within the given range for the launch parameters, efficiency markedly increases with the growth in the problem size. Taking into account that the difference between maximum and minimum efficiency is nearly 80 percent, we can also make the conclusion that the increase in efficiency regarded as a function of problem size is observed over the greater part of the range covered.
- Along two directions: 0.0000284. Suppose that both the computational complexity and the number of processes increase over the entire region under discussion. Then the efficiency increases; however, the increase in efficiency is not very significant.