Tarjan-Vishkin biconnected components algorithm
| Алгоритм Тарьяна-Вишкина поиска компонент двусвязности/мостов в графе | |
| Sequential algorithm | |
| Serial complexity | [math]O(|V| + |E|)[/math] |
| Input data | [math]O(|V| + |E|)[/math] |
| Output data | [math]max O(|V|)[/math] |
| Parallel algorithm | |
| Parallel form height | [math]N/A [/math] |
| Parallel form width | [math] O(|V|) [/math] |
Primary author of this description: I.V.Afanasyev.
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 2.1 Implementation peculiarities of the serial algorithm
- 2.2 Locality of data and computations
- 2.3 Possible methods and considerations for parallel implementation of the algorithm
- 2.4 Scalability of the algorithm and its implementations
- 2.5 Dynamic characteristics and efficiency of the algorithm implementation
- 2.6 Conclusions for different classes of computer architecture
- 2.7 Existing implementations of the algorithm
- 2.8 Conclusions for different classes of computer architecture
- 2.9 Existing implementations of the algorithm
1 Properties and structure of the algorithm
1.1 General description of the algorithm
Параллельный алгоритм Тарьяна-Вишкина [1] находит компоненты двухсвязности неориентированного графа за время [math]O(\ln |V|)[/math] на [math]O(|V| + |E|)[/math] процессорах. Алгоритм может быть адаптирован для поиска мостов. Эффективность алгоритма Тарьяна-Вишкина подтверждена в последнее время[2][3] как на системах архитектуры SMP, так и при вычислениях на GPU.
1.2 Mathematical description of the algorithm
1. Для каждой компоненты связности графа найти какое-либо остовное дерево [math]T[/math].
2. Перенумеровать вершины [math]T[/math] в порядке обратного обхода.
3. В порядке возрастания номера вершины выполнить следующие действия:
a. [math]D(v) := 1+ \sum_{v \rightarrow w}D(w) [/math]
b. [math] L(v) := \min { \{N(v) - D(v)+1 \} \cup \{ L(w) | v \rightarrow w \} \cup \{ N(w) | v \cdots w \} }[/math]
c. [math] H(v) := \max { \{ N(v) \} \cup \{ H(w) | v \rightarrow w \} \cup \{ N(w) | v \cdots w \} }[/math]
d. Пометить ребро [math]v \rightarrow w[/math] мостом, если [math]H(w)\lt =N(w)[/math] и [math]L(w)\gt N(w)-D(w)[/math].
1.3 Computational kernel of the algorithm
Вычислительно затратной частью алгоритма является поиск в ширину, вычисляющий величины [math]N(v)[/math], вычислительным ядром которого является обход вершин, смежной к выбранной вершине [math]v[/math] с последующем добавлением еще не посещенных вершин в множество [math]P[/math]. Данная операция выполняться на каждом шаге для каждой вершины [math]v[/math] графа.
1.4 Macro structure of the algorithm
На первом шаге работы алгоритма строится остовный лес графа с использованием модифицированного алгоритма Шилоаха-Вишкина.
Для этого для каждой вершины [math]v[/math] определяется указатель на родительскую вершину [math]P(v)[/math]; на шаге инициализации [math]P(v):=v[/math]. Далее остовный лес строится чередованием двух параллельных операций:
• Удвоение указателей: [math]P(v):=P(P(v))[/math] ;
• Соединение: [math]P(P(v)):=P(w)[/math], где [math]v[/math] – вершина [math]P[/math]-дерева ( [math]P(v)=v[/math]на текущем шаге), [math]w[/math]– некоторая вершина, для которой существует ребро [math](v,w)\in E[/math]. Ребро помечается, как принадлежащее остовному лесу .
Далее производятся следующие шаги:
• перенумерация вершин в обратном порядке обхода (post-order);
• вычисление количества потомков [math]D(v)[/math] для каждой вершины;
• вычисление значений [math]L(v)[/math] и [math]H(v)[/math] для каждой вершины;
• пометка рёбер [math]v \rightarrow w[/math] мостами, если [math]H(w)\lt =N(w)[/math] и [math]L(w)\gt N(w)-D(w)[/math].
Основной идеей для обеспечения завершения работы алгоритма за [math]O( \ln |V|)[/math] шагов является систематическое использование операции удвоения указателей.
1.5 Implementation scheme of the serial algorithm
На первом шаге работы алгоритма строится остовный лес графа при помощи последовательных вызовов поисков в ширину от еще не посещенных на предыдущих шагах вершин. При необходимости может быть выполнен шаг Trim, выделяющий вершины, принадлежащие связанным компонентам единичного размера.
После этого производится построение островного дерева при помощи поиска в глубину, с подсчетом величин [math]D(v)[/math].
Затем производятся вычисления величин [math]L[/math] и [math]H[/math] по формулам, приведенным в пунктах b,c в предыдущем разделе.
1.6 Serial complexity of the algorithm
Последовательный вариант алгоритма аналогичен алгоритму Тарьяна[4] и имеет линейную сложность [math]O(|E| + |V|)[/math].
1.7 Information graph
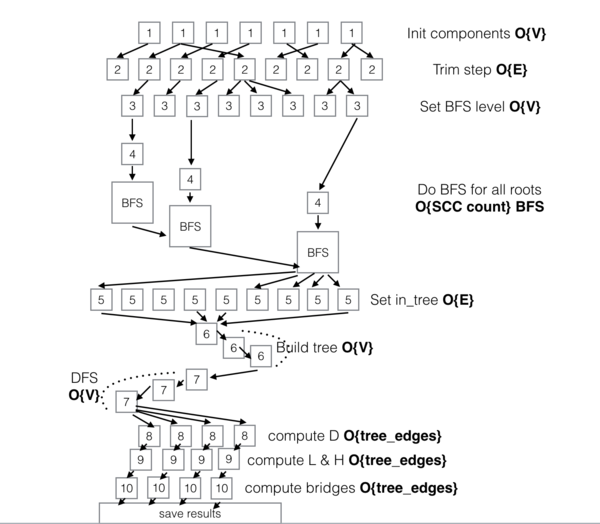
Далее на рисунке 1 представлен информационный граф алгоритма, демонстрирующий его основные уровни параллелизма.
В начале работы производится инциализация связанных компонент графа [1] и выделение тривиальных компонент (размера 1 и 2) [2], затем инициализация уровней для всех вершин [3] и последовательные поиски в ширину [4],[BFS] до тех пор, пока все вершины не будут размечены различными уровнями.
Далее происходит поиск ребер, которые войдут в остовное дерево [5] и последовательное построение данного дерева на основе поиска в глубину [6],[7]. Затем друг за другом вычисляются необходимые метрики для каждой их вершин L, H и D [8],[9]. В конце на основе данных метрик вычисляются мосты в графе [10].
1.8 Parallelization resource of the algorithm
Алгоритм изначально параллельный, время работы [math]O(\ln(|V|))[/math] на [math]O(|V| + |E|)[/math] процессорах.
Изначальные инициализации компонент и уровней вершин [1] и [3] могут выполняться параллельно за [math]O(|V|)[/math] операций. Шаг трим [2] так же может быть выполнен за [math]O(|E|)[/math] параллельных атомарных операций. Поиски в ширину от каждой корневой вершины [4],[BFS] производятся последовательно друг за другом, однако сами поиски в ширину обладают значительным образом параллелизма, описанным в соответствующем разделе.
Нумерация вершин [math]D(v)[/math] в порядке обходе графа поиском в глубину [5],[6] должно выполняться сугубо последовательно за [math]O(|V|)[/math] операций, и может, вообще говоря, серьезно снизить производительность реализации на параллельных архитектурах.
Вычисление величин [math]L[/math], [math]H[/math] и ребер, являющихся мостами [8],[9],[10] может выполняться каждое за [math]O(|V|)[/math] операций.
Таким образом, ширина ярусно-параллельной формы алгоритма равна [math]O(|E|)[/math], а высота ЯПФ, вообще говоря, зависит от структуры входного графа (числа связанных компонент, и, как следствие, числа необходимых поисков в ширину).
1.9 Input and output data of the algorithm
Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math].
Объём входных данных: [math]O(|V| + |E|)[/math].
Выходные данные
Список ребер, являющихся мостами в графе.
Объём выходных данных:
1. [math]O(|E|)[/math] в случае хранения массива принадлежности каждого ребра к множеству мостов в графе
2. [math]max O(|V|)[/math] в случае хранения мостов в виде списка пар вершин
1.10 Properties of the algorithm
1. Компонента сильной связности – подграф, любые две вершины которого принадлежат какому-либо циклу, и содержащий все такие циклы для своих вершин.
2. Компонента сильной связности является объединением всех циклом, проходящих через её вершины.
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
2.2 Locality of data and computations
2.2.1 Locality of implementation
2.2.1.1 Structure of memory access and a qualitative estimation of locality
2.2.1.2 Quantitative estimation of locality
2.3 Possible methods and considerations for parallel implementation of the algorithm
Программа, реализующая алгоритм Тарьяна-Вышкина, состоит из двух частей: CPU части, отвечающей за параллельные вычисления на многоядерных CPU, а так же копирование данных на GPU и общее управлениями вычислениями, и GPU части, отвечающей только за вычисления на графическом ускорителе.
2.4 Scalability of the algorithm and its implementations
2.4.1 Scalability of the algorithm
2.4.2 Scalability of of the algorithm implementation
Проведём исследование масштабируемости параллельной реализации алгоритма Тарьяна-Вишкина согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов-2 Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- размер графа [2^18 : 2^26].
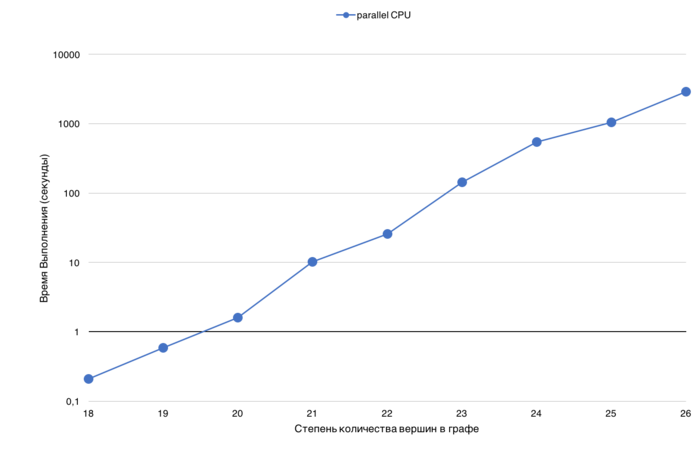
Проведем отдельные исследования масштабируемости вширь реализации алгоритма Тарьяна-Вишкина.
Основной характеристикой для сравнения было выбрано время выполнения, так как производительность (определения как TEPS то есть число ребер графа, которое алгоритм обрабатывает в секунду) для данной операции не отражает реальную эффективность обработки.
Анализируя время выполнения можно оценить, насколько понижается эффективность обработки графа при увеличении его размера (данные перестают помещаться в кэш, в память GPU, узла и т.д.).
2.5 Dynamic characteristics and efficiency of the algorithm implementation
2.6 Conclusions for different classes of computer architecture
2.7 Existing implementations of the algorithm
2.8 Conclusions for different classes of computer architecture
2.9 Existing implementations of the algorithm
- ↑ Tarjan, Robert Endre, and Uzi Vishkin. “An Efficient Parallel Biconnectivity Algorithm.” SIAM Journal on Computing 14, no. 4 (1985): 862–74.
- ↑ Edwards, James A, and Uzi Vishkin. “Better Speedups Using Simpler Parallel Programming for Graph Connectivity and Biconnectivity,” PMAM’12, 103–114, New York, USA: ACM Press, 2012. doi:10.1145/2141702.2141714
- ↑ Guojing Cong, and David A Bader. “An Experimental Study of Parallel Biconnected Components Algorithms on Symmetric Multiprocessors (SMPs),” 45b, IEEE, 2005. doi:10.1109/IPDPS.2005.100.
- ↑ Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.