Poisson equation, solving with DFT, scalability

Primary author of this description: V.M.Stepanenko, E.V.Mortikov.

1 Links

For the experiments, we used the implementation of the algorithm for solving the Poisson equation by the discrete Fourier transform.

3 Scalability of the algorithm and its implementations

3.2 Scalability of of the algorithm implementation

The variable start-up parameters of this implementation and their ranges are as follows:

• the number of processors is a squared integer in the range [4 : 100];
• the domain size varies in the range [100x100x100 : 250x100x100] with the step 50x100x100.

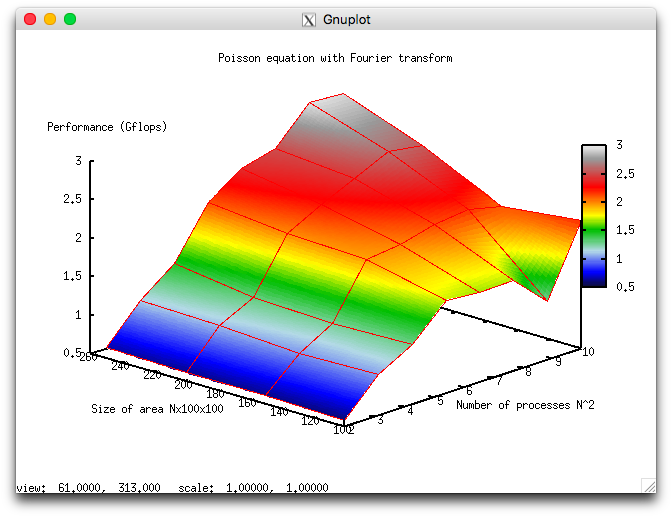
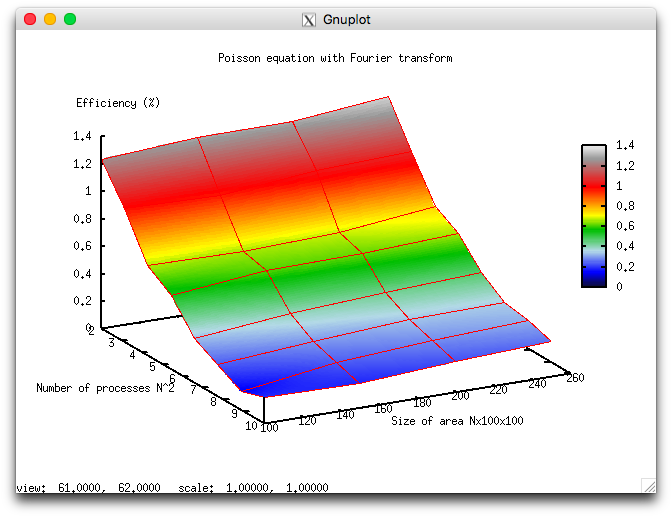
The experiments resulted in the following range for the implementation efficiency of this algorithm:

• the minimum efficiency is 0,132%;
• the maximum efficiency is 1,34%.

The following two figures show how the performance and efficiency of this implementation depend on the variable start-up parameters.

Figure 1. Parallel implementation of the algorithm. Performance as a function of the number of processors and the domain size.

Figure 2. Parallel implementation of the algorithm. Efficiency as a function of the number of processors and the domain size.

These results are in good qualitative agreement with the estimates given in the preceding section. For instance, one can see from fig. 8 that the scalability of the algorithm improves with the growth of [math]N[/math]; that is, the performance improves faster with the growing number of cores. This is consistent with the fact that [math]\alpha[/math] decreases with the growth of [math]N[/math], although the dependence revealed by the expression [math]\alpha=12/(6\log_2 N+1)[/math] is considerably more weak. On the whole, the scalability of the algorithm is rather weak. Suppose that the domain has the size 250х100х100. When the number of cores increases by a factor 25 (from 4 to 100), the performance of calculations increases only sixfold.