DCSC algorithm for finding the strongly connected components

Алгоритм DCSC поиска компонент сильной связности
Sequential algorithm
Serial complexity	[math]O(|V| \ln(|V|))[/math]
Input data	[math]O(|V| + |E|)[/math]
Output data	[math]O(|V|)[/math]
Parallel algorithm
Parallel form height	[math]C * O(ln(u))[/math]
Parallel form width	[math]O(|E|)[/math]

Primary author of this description: I.V.Afanasyev.

1 Properties and structure of the algorithm

1.1 General description of the algorithm

Алгоритм DCSC (Divide and Conquer Strong Components) finds strongly connected components of a directed graph with the expected complexity [math]O(|V| \ln |V|)[/math] (assuming that the node degrees are bounded by a constant).

In the literature on GPU implementations of the algorithm, it is typically called the Forward-Backward algorithm (shortly, the FB-algorithm).

From the outset, the algorithm was designed for parallel realization. Indeed, at each step, it finds a strongly connected component and selects up to three subsets in the graph that contain other connected components and can be processed in parallel. Moreover, the selection of these subsets and the strongly connected component can be done in parallel (using parallel breadth-first searches). It should be noted that the iterations of breadth-first searches need not to be synchronized because their aim is to determine reachable nodes rather than to find the distances to these nodes.

The algorithm is well suitable for graphs that consist of a small number of large strongly connected components. A significant increase in the number of strongly connected components implies that the complexity of the algorithm also increases significantly (proportionally to the number of components). For this reason, the algorithm may become less efficient than Tarjan's algorithm, which selects strongly connected components in the course of one graph traversal.

The following modification of the algorithm was proposed to improve its efficiency for graphs with a large number of trivial (that is, of size 1 or 2) strongly connected components: prior to executing the classical algorithm, the so-called Trim step is performed. This step, described in a later section, allows one to select all the trivial strongly connected components. For instance, for RMAT graphs, an application of the Trim step leaves in the graph only a few large strongly connected components. For such components, the complexity of the algorithm is not large.

1.2 Mathematical description of the algorithm

Let [math]v[/math] be a node of the graph. Define the following sets of nodes:

⎯ [math]Fwd(v)[/math] – the nodes reachable from [math]v[/math] .

⎯ [math]Pred(v)[/math] – the nodes from which [math]v[/math] is reachable (equivalently, the nodes reachable from [math]v[/math] in the graph obtained by reverting all the arcs in [math]G[/math]).

By using these sets, all the nodes of the graph can be partitioned into four regions:

⎯ [math]V_1 = Fwd(v) \cap Pred(v) [/math]

⎯ [math]V_2 = Fwd(v) \setminus Pred(v) [/math]

⎯ [math]V_3 = Pred(v) \setminus Fwd(v)[/math]

⎯ [math]V_4 = V \setminus Pred(v) \setminus Fwd(v)[/math]

Then one can assert the following:

1. The region [math]V_1[/math] is a strongly connected component.

2. Every other strongly connected component is completely contained in one of the regions [math]V_2[/math], [math]V_3[/math], or [math]V_4[/math].

1.3 Computational kernel of the algorithm

The basic computational operations of the algorithm are the search for nodes reachable from the chosen node [math]v[/math] and the search for nodes from which [math]v[/math] is reachable. Both these operations can be implemented by using breadth-first searches in the following manner:

1. The node [math]v_0[/math] is placed at the beginning of queue and marked as a visited node.

2. Remove the front node [math]v[/math] from the queue. For all the arcs [math](v, u)[/math] outcoming from [math]v[/math], verify whether the node [math]u[/math] was visited. If it was, then [math]u[/math] is placed at the beginning of queue.

3. As long as the queue is not empty, go to step 2.

1.4 Macro structure of the algorithm

The DCSC algorithm consists of the following actions:

1. Place the set [math]V[/math] to a queue.

2. Process the queue in parallel. For each element in [math]V[/math]:

(a) Choose an arbitrary pivot node [math]v \in V[/math].

(b) Compute the sets [math]Fwd(v)[/math] and [math]Pred(v)[/math] (these two computations can be executed in parallel; in addition, as indicated above, each of them is well parallelizable).

(c) Add the set [math] V_1[/math] to the list of strongly connected components.

(d) Add the sets [math] V_2[/math], [math]V_3[/math], and [math]V_4[/math] to the queue.

3. The algorithm terminates when the queue is empty and there are no active processes left.

To improve the balance of loading at the first steps of the algorithm, one can simultaneously choose several pivot nodes rather than a single node. If these pivots belong to different strongly connected components, then the result is a partition of the graph into numerous regions, which thereafter are processed in parallel.

An important modification of the DCSC algorithm consists in executing a Trim step before the basic calculations. The Trim step can be described as follows:

1. Mark all [math]v \in V[/math] as active nodes.

2. For each node [math]v[/math], calculate the number [math]in(v)[/math] of incoming arcs and the number [math]out(v)[/math] of outcoming arcs [math](v, u) \in E[/math] such that [math]u[/math] is an active node.

3. Mark as nonactive all the nodes [math]v \in V[/math] for which at least one of the numbers [math]in(v)[/math] and [math]out(v)[/math] is zero.

4. Go to step 2 until the number of active nodes ceases to very.

Moreover, the chosen scheme for storing the graph may require that the transpose of this graph be first constructed. This may make more efficient the implementation of the Trim step and the search (within the computational kernel of the algorithm) for nodes from which the given node [math]v[/math] is reachable.

1.5 Implementation scheme of the serial algorithm

The serial algorithm is implemented by the following pseudocode:

Input data:
  graph with nodes V and arcs E;
Output data: indices of the strongly connected components c(v) for each node v ∈ V.

compute_scc_with_trim(G)
{
	G’ = transpose(G)
	G = trim(G)
	compute_scc()
}

compute_scc(V, G, G’)
{
	p = pivot(V)

	fwd = bfs(G, p);
	pred = bfs(G’, p);

	compute_scc(fwd / pred, G, G’)
	compute_scc(pred / fwd, G, G’)
	compute_scc(V / pred / fwd, G, G’)
}

pivot(V)
{
	return random v in V
}

trim(G)
{
	for each v in V(G)
		active[v] = true

	changes = false
	do
	{
		for each v in V
			in_deg(v) = compute_in_degree(v)
			out_deg(v) = compute_out_degree(v)
		
		for each v in V
			if (in_deg[v] == 0 || out_deg[v] == 0)
				active[v] = false
				changes = true
	} while (!changes)
	return active
}

Here, bfs are conventional breadth-first searches described in the corresponding section. Such a search results in finding all the nodes of the graph [math] G [/math] that are reachable from the given node [math] p [/math].

1.6 Serial complexity of the algorithm

Assume that all the nodes of a graph have degrees bounded by a constant. Then the expected serial complexity of the algorithm is [math]O(|V| \ln(|V|))[/math].

1.7 Information graph

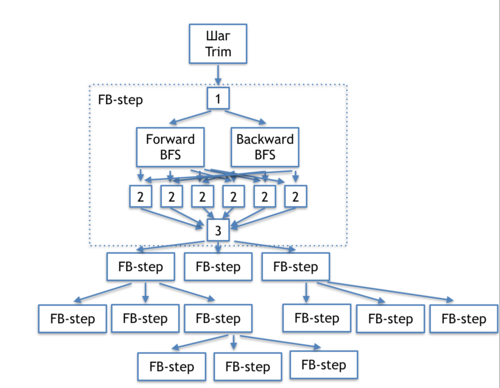
The information graph of the DCSC algorithm shown in figure 1 demonstrates relations between the basic parts of the algorithm.

Figure 1. Information graph of the DCSC algorithm (Forward-Backward-Trim).

These basic parts are: initial Trim step; choice of the pivot node [1]; breadth-first searches performed in the direct graph and its transpose (forward и backward BFS); handling the results of searches [2]; test for the necessity to continue the recursion [3]; and recursive calls of the FB-step. Below, we present more detailed information graphs for each of the parts, as well as the transcript of the corresponding operations. In the next section, we assess the parallelization resource of each part.

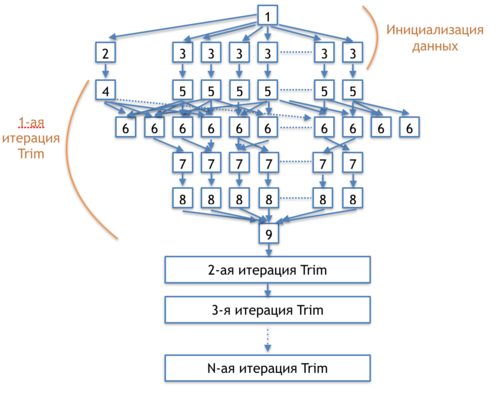
The information graph of the Trim step is shown in figure 2.

Figure 2. Information graph of the Trim step in the DCSC algorithm.

[1] - memory allocation for the arrays storing the numbers of incoming and outcoming arcs and the array of active nodes

[2] - initialization of the variable "change indicator"

[3] - initialization of the array for strongly connected components and the array of active nodes

[4] - assignment of the value "no changes" to the change indicator

[5] - zeroing out the arrays for the numbers of incoming and outcoming arcs

[6] - verification whether the nodes at the ends of each arc are active; increasing the number of incoming/outcoming arcs for the corresponding nodes; update the value of the change indicator

[7] - activity test for all the nodes of the graph

[8] - numbering of the strongly connected components with zero degree of incoming or outcoming arcs

[9] - verification whether any changes occurred at step 6; transition to the next iteration

The information graph of the BFS stage (Forward и Backward BFS) is shown at the corresponding section (Breadth_first_search_(BFS)).

1.8 Parallelization resource of the algorithm

From the outset, the algorithm was designed for parallel realization. It has several levels of parallelism.

На верхнем уровне алгоритм DCSC может параллельно выполнять FB-шаги, продемонстрированные на рисунке 1. Таким образом, на каждом рекурсивном шаге алгоритма могут рекурсивно порождаться до 3 новых параллельных процессов, общее число которых равно числу сильно связанных компонент графа. Кроме того, поиски в ширину в исходном и транспонированном графах независимы и также могут выполняться параллельно друг с другом. Таким образом, на верхнем уровне может выполняться до [math] 2*u/log|u|[/math] параллельных потоков, где [math] u [/math] - это число сильно связанных компонент графа. Важно заметить, что вычисления FB-шагов одного уровня (а также всех последующих рекурсивных) абсолютно независимы по данным, так как производятся в непересекающихся множествах вершин графа, поэтому могут производиться в том числе и на различных узлах. Кроме того, составные шаги алгоритма (поиск в ширину и шаг Trim) также имеют значительный потенциал параллелизма, описанный далее.

Этап Trim алгоритма, информационный граф которого приведен на рисунке 2, обладает значительным ресурсом параллелизма: единственной последовательной частью является инициализация массивов и переменных (1)(2), а так же проверка условия выхода из цикла (9). Операции (3),(5),(7) и (8) абсолютно независимы и могу производиться параллельно, их число составляет [math]O(|V|)[/math]. Проверки и обновления данных в операции (6) так же могут производиться параллельно, однако обновления данных должны производиться атомарно. Число операций (6) равно [math]O(E)[/math]. Таким образом, почти все операции шага Trim могут выполняться параллельно, при том число параллельно выполняемых операций составляет [math]|V|[/math] или [math]|E|[/math]. Учитывая, что величины [math]|V|[/math] и [math]|E|[/math] для графов большого размера крайне велики, потенциал параллелизма данной части алгоритма очень значителен и достаточен для полной загрузки современных вычислительных узлов/сопроцессоров. Кроме того, операции (3),(5),(7),(8) могут быть успешно векторизованы.

Ресурс параллелизма операции поиска в ширину подробно описан в соответвующем разделе (Поиск_в_ширину_(BFS)). В зависимости от выбора формата хранения графа, подход к параллельной реализации поиска в ширину может быть линейным или квадратичным (в худшем случае).

В случае линейного подхода, на каждом алгоритма шаге поиска в ширину может выполняться [math]O(n)[/math] параллельных операций, где [math]n[/math] - это число вершин, добавленных для просмотра на предыдущем шаге. Перед началом работы алгоритма для просмотра добавляется вершина-источник, на первом шаге - все еще не посещенные смежные с ней, на втором - все еще не посещенные смежные с вершинами на первом шаге, и.т.д. Максимальное (или даже среднее) число вершин а каждом шаге оценить проблематично, так как число шагов алгоритма, число достижимых вершин, а так же структура связей между ними определены лишь структурой конкретного входного графа. В случае, если все вершины достижимы, а число шагов поиска в ширину составляет [math] r [/math], то среднее число параллельно обрабатываемых вершин на каждом шаге составляет [math] O(|V|)/r [/math]. Важно заметить, что наибольший уровень параллелизма достигается на средних шагах алгоритма, в то время как число вершин для обработки на начальных и конечных шагах может быть небольшим.

В случае квадратической параллелизации алгоритм поиска в ширину на каждом шаге обходит все ребра графа, таким образом выполняя [math]O(|E|)[/math] параллельных операций, что совпадает с аналогичной оценкой для шага trim. Кроме того, поиск в ширину при реализации с использованием формата списка ребер графа может быть векторизован.

Таким образом, на начальном этапе алгоритма может выполняться [math]O(|V|)[/math] или [math]O(|E|)[/math] параллельных операций. Далее следует [math]O(log(u))[/math] шагов, в каждом из которых в среднем присутствует [math]2*u/O(log(u))[/math] поисков в ширину, которые так же обладают внутренним ресурсом параллелизма: каждый поиск в ширину имеет [math]O(|E|)[/math] параллельных операций на каждом шаге при квадратическом подходе к параллелизации.

Высота и ширина ярусно-параллельной формы зависит от структуры графа (числа и расположения сильно связанных компонент), по причине аналогичной зависимости шагов FB_step от входных данных.

1.9 Input and output data of the algorithm

Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math].

Объём входных данных: [math]O(|V| + |E|)[/math].

Выходные данные: для каждой вершины [math]v[/math] исходного графа – номер компоненты сильной связанности, в которую входит данная вершина [math] c(v) [/math], вершины, принадлежащие одной компоненте сильно связанности имеют одинаковые номера

Объём выходных данных: [math]O(|V|)[/math].

1.10 Properties of the algorithm

Вычислительное ядро алгоритма основано на поисках в ширину, поэтому многие свойства (локальности, масштабируемости) этих алгоритмов так же схожи.

2 Software implementation of the algorithm

2.4 Scalability of the algorithm and its implementations

2.4.1 Scalability of the algorithm

Алгоритм обладает значительным потенциалом масштабируемости, так как, во-первых, поиск в ширину, на котором он основывается, поддается эффективному распараллеливанию либо при помощи квадратичнго подхода, либо при помощи параллельных очередей (по очереди на процессор).

Кроме того, дополнительный ресурс параллелизма можно получить при параллельной обработке трех получающихся множеств вершин на каждом шаге алгоритма, использую задачи и nested parallelism.

2.4.2 Scalability of of the algorithm implementation

Проведём исследование масштабируемости параллельной реализации алгоритма Forward-Backward-Trim согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов-2 Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

число процессоров [1 : 28] с шагом 1; размер графа [2^20 : 2^27].

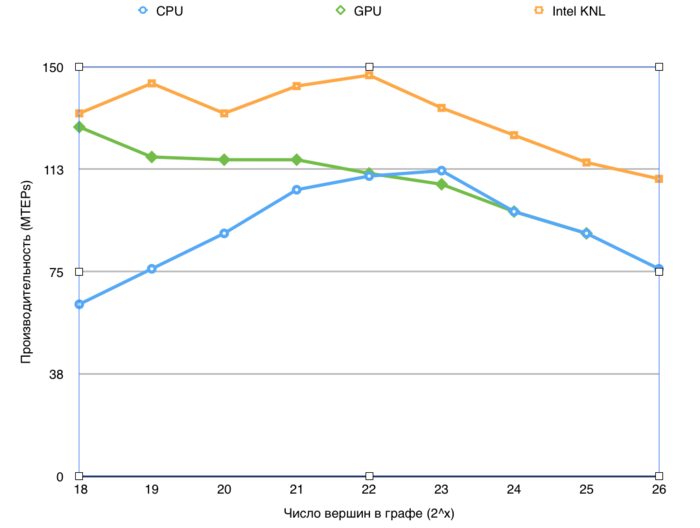
Проведем отдельные исследования сильной масштабируемости вширь указанной реализации.

Производительность определена как TEPS (от англ. Traversed Edges Per Second), то есть число ребер графа, который алгоритм обрабатывает в секунду. С помощью данной метрики можно сравнивать производительность для различных размеров графа, оценивая, насколько понижается эффективность обработки графа при увеличении его размера.

Рисунок 3. Параллельная реализация алгоритма Farward-Backward-Trim, масштабируемость различных версий реализации алгоритма: производительность в зависимости от размера графа

2.7 Existing implementations of the algorithm

• C++, MPI: Parallel Boost Graph Library (функция strong_components), распределённый алгоритм DCSC сочетается с локальным поиском компонент сильной связности алгоритмом Тарьяна.