Cooley–Tukey Fast Fourier Transform, radix-2 case

Primary authors of this description: A.V.Frolov, Vad.V.Voevodin (Section 2.2), A.M.Teplov (Section 2.4)

1 Description of the properties and structure of the algorithm

1.1 General description

Simple Cooley-Tukey algorithm is a variant of Fast Fourier Transform intended for complex vectors of power-of-two size and avoiding special techniques used for sizes equal to power of 4, power of 8, etc. The algorithm repeatedly applies the Fast Fourier Transform and reduces the entire process to a sequence of Fourier transforms of size 2 and multiplications by the so-called twiddle factors. It is slower than Cooley-Tukey algorithms that express a power-of-two size as a power of 4, power of 8, etc. and then use special features of these cases. Nevertheless, this algorithm is widespread for the reason that its program implementation is the simplest of all FFT implementations.

1.2 Mathematical description

Input data: complex vector to be transformed [math]a[/math] (with components [math]a_{i}[/math]).

Output data: complex vector [math]b[/math] (with components [math]b_{i}[/math]), the result of the transform

The size (dimension) of the vectors is [math]n[/math]; moreover, [math]n = 2^l[/math]

1.2.1 Recursive description

The input vector is first written as a sequence of rows, each row containing only two components. Then each row undergoes the Fourier transform of size two. The resulting elements are multiplied by the twiddle factors [math]exp (2 \pi i(m-1)(j-1)/n)[/math] ([math]m[/math] is the row index, and [math]j[/math] is the column index). Finally, each column is processed by the FFT of size [math]n/2[/math]. For the first column, the twiddle factors are equal to 1; hence, no actual multiplication is performed. For the second column, the multiplication by the twiddle factors is combined with the Fourier transform of size two. This combination, called a butterfly by the FFT experts, is the basic operation of the simple Cooley-Tukey algorithm. The butterfly consists in adding two complex numbers and calculating their difference with the subsequent multiplication by another complex number. On the whole, there are [math]n/2[/math] butterflies at each step, while the number of steps is [math]l-1[/math]. Only sums and differences are calculated at the last step [math]l[/math].

1.2.2 Trigonometric functions

Although the calculations described above use the twiddle factors [math]exp (2 \pi i(m-1)(j-1)/n)[/math], it is unreasonable to calculate them while executing the Cooley-Tukey algorithm. Otherwise, the calculations of sines and cosines would constitute the lion's share of all calculations in the algorithm. Usually (and similarly to the other versions of FFT), the twiddle factors are pre-calculated and stored in a separate array. We assume here that the algorithm is executed in exactly this form.

1.3 Computational kernel of the algorithm

The computational kernel of the algorithm is compiled of butterflies. Each butterfly consists in adding two complex numbers and calculating their difference with the subsequent multiplication by another complex number. There are on the whole [math](1/2) n log_{2} n [/math] butterflies. No multiplications are performed in [math]n/2[/math] butterflies.

1.4 Macrostructure of the algorithm

The macrostructure of the algorithm can best of all be described in a recursive manner, namely, as [math]n/2[/math] Fourier transforms of size two, the multiplication of [math]n/2[/math] pairs of complex numbers, and two FFTs of size [math]n/2[/math].

1.5 Implementation scheme of the serial algorithm

Under the nonrecursive organization scheme, the execution of a butterfly is preceded by partitioning the components into [math]n/2[/math] pairs (there are on the whole [math]log_{2} n [/math] butterflies). At each step, the difference of indices of the elements in a pair is doubled. This difference is 1 at the first step and [math]n/2[/math] at the last step. The result of addition is written into the component with a lesser index, while the result of subtraction and subsequent multiplication is written into the component with a larger index.

1.6 Serial complexity of the algorithm

If the serial complexity is determined by considering only the principal terms of the number of operations, then the simple Cooley-Tukey algorithm requires [math]n log_{2} n[/math] complex additions and [math](1/2) n log_{2} n [/math] complex multiplications. Thus, the simple Cooley-Tukey algorithm can be qualified as a linear logarithmic complexity algorithm.

1.7 Information graph

The simple Cooley-Tukey algorithm for n=8. Op+ denotes the addition of two complex numbers, while Op- denotes the subtraction of two complex numbers followed by multiplying the result by another complex number (a twiddle factor). No multiplications occur in the last column. The vertices of the graph correspond to the parameter of the outer loop along the horizontal axis and the components of the array along the vertical axis.

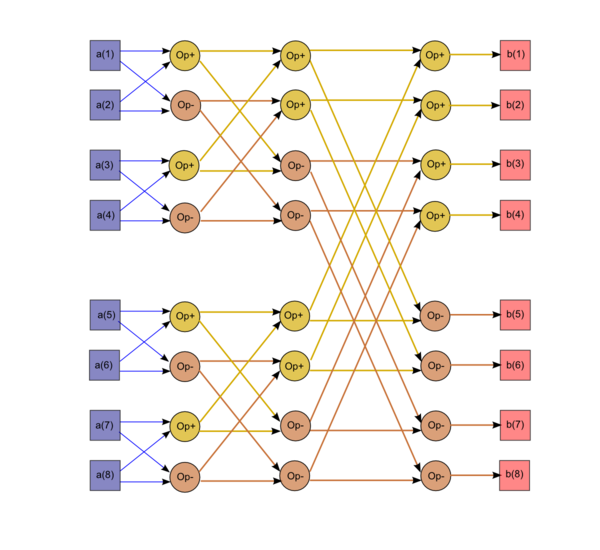
It is evident from the figure that this graph is not linear either in the size or in formulas for its edges. The size of the graph is linear logarithmic, while the edge formulas contain exponentials. At the i-th step, each butterfly involves two components whose indices in their binary representation differ only in the (i-1)-th bit.

1.8 Parallelism resource of the algorithm

If only the principal terms of the number of operations are considered, then the simple Cooley-Tukey algorithm has a critical path formed of [math]log_{2} n [/math] complex additions/subtractions and [math]log_{2} n [/math] complex multiplications. Thus, in terms of parallel complexity, the simple Cooley-Tukey algorithm can be placed into the logarithmic class. In terms of the parallel form width, the complexity of the algorithm is "linear.

1.9 Description of the input and output data

Input data: vector [math]a[/math] (with components [math]a_{i}[/math]).

Size of the input data: [math]n[/math] .

Output data : vector [math]b[/math] (with components [math]b_{i}[/math]).

Size of the output data: [math]n[/math].

1.10 Properties of the algorithm

It is clear that, in the case of unlimited resources, the ratio of the serial to parallel complexity is linear.

The computational power of the algorithm, understood as the ratio of the number of operations to the total size of the input and output data, is logarithmic.

The algorithm is completely determined.

Note that the simple Cooley-Tukey algorithm is not optimal even for vectors of power-of-two size. However, we do not consider any other FFT algorithms here.