Cooley–Tukey Fast Fourier Transform, radix-2 case

Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (раздел 2.2)

1 Описание свойств и структуры алгоритма

1.1 Общее описание алгоритма

Простой алгоритм Кули-Тьюки - один из вариантов быстрого преобразования Фурье для комплексных векторов с размерностью, равной степени двойки, без использования специфичных приёмов, использующихся для степеней четвёрки, восьмёрки и др. Заключается в последовательном применении метода быстрого преобразования Фурье и сведении преобразования к последовательности преобразований Фурье размерности 2 и выполнения умножений на т.н. поворотные множители. Несмотря на то, что проигрывает алгоритмам Кули-Тьюки, разлагающим степени двойки на степени 4, 8 и др. и использующим их специфику, весьма распространён, что связано с самой простой из алгоритмов БПФ записью программной реализации.

1.2 Математическое описание

Исходные данные: преобразуемый комплексный вектор [math]a[/math] (элементы [math]a_{i}[/math]).

Вычисляемые данные: комплексный вектор - результат преобразования [math]b[/math] (элементы [math]b_{i}[/math]).

При этом размерность векторов - [math]n[/math], причём [math]n = 2^l[/math]

1.2.1 Рекурсивное описание

Вектор записывается по строкам по 2 элемента в каждой. После этого над каждой строкой выполняется преобразование Фурье порядка 2, получившиеся элементы умножаются на поворотные множители [math]exp (2 \pi i(m-1)(j-1)/n)[/math] ([math]m[/math] - номер строки, [math]j[/math] - номер столбца), после чего выполняется БПФ порядка [math]n/2[/math] над каждым из столбцов. Поскольку для 1-го столбца поворотные множители равны 1, то реально умножение на них не выполняется, а умножения на поворотные множители элементов второго столбца соединяются с преобразованием Фурье порядка 2. Эта комбинация, называемая "бабочкой" в среде специалистов по БПФ, и является основной операцией в простом алгоритме Кули-Тьюки. "Бабочка" состоит из вычисления суммы двух комплексных чисел, а также из вычисления их разности с последующим умножением на комплексное число. Всего на каждом шаге выполняется [math]n/2[/math] "бабочек", а шагов - [math]l-1[/math]. Последний, [math]l[/math]-й шаг вычисляет только суммы и разности.

1.2.2 Тригонометрические функции

Несмотря на то, что в вычислениях используются поворотные множители [math]exp (2 \pi i(m-1)(j-1)/n)[/math], нецелесообразно вычислять их в процессе выполнения алгоритма Кули-Тьюки, поскольку вычисления косинусов и синусов (в мнимой экспоненте) тогда составили бы львиную долю вычислений алгоритма. Поэтому обычно (как и в других версиях БПФ) поворотные множители вычисляются заранее и хранятся в специальном массиве. Здесь мы будем предполагать, что алгоритм выполняется именно так.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма составляют "бабочки", состоящие из вычисления суммы двух комплексных чисел, а также из вычисления их разности с последующим умножением на комплексное число. Всего их [math](1/2) n log_{2} n [/math] штук, при этом в [math]n/2[/math] из них умножение не выполняется.

1.4 Макроструктура алгоритма

Макроструктура алгоритма лучше всего описывается рекурсивно, как [math]n/2[/math] преобразований Фурье порядка 2, умножение [math]n/2[/math] пар комплексных чисел и затем 2 БПФ порядка [math]n/2[/math].

1.5 Описание схемы реализации последовательного алгоритма

Нерекурсивная схема организации состоит в том, что на каждом шаге (а всего их [math]log_{2} n [/math]) для выполнения "бабочки" все элементы разбиваются на [math]n/2[/math] пар. В зависимости от номера шага, разница координат для каждой пары элементов удваивается. На первом шагу она равна 1, на последнем - [math]n/2[/math]. При этом результат суммы записывается в элемент с меньшим номером, а результат вычитания с последующим умножением - в элемент с большим.

1.6 Последовательная сложность алгоритма

Если считать только главные члены выражений для последовательной сложности алгоритма, то простой алгоритм Кули-Тьюки может быть выполнен за [math]n log_{2} n[/math] операций комплексного сложения и [math](1/2) n log_{2} n [/math]операций комплексного умножения. Таким образом, простой алгоритм Кули-Тьюки может быть отнесён к линейно-логарифмическому классу по последовательной сложности.

1.7 Информационный граф

Простой алгоритм Кули-Тьюки для n=8. Op+ - операция сложения двух комплексных чисел. Op- - операция вычитания двух комплексных чисел и умножения результата вычитания на комплексное число (поворотный множитель). В последнем столбце операций умножение не производится. Привязка вершин выполнена по оси абсцисс - к параметру внешнего цикла, по оси ординат - к обрабатываемым элементам массива

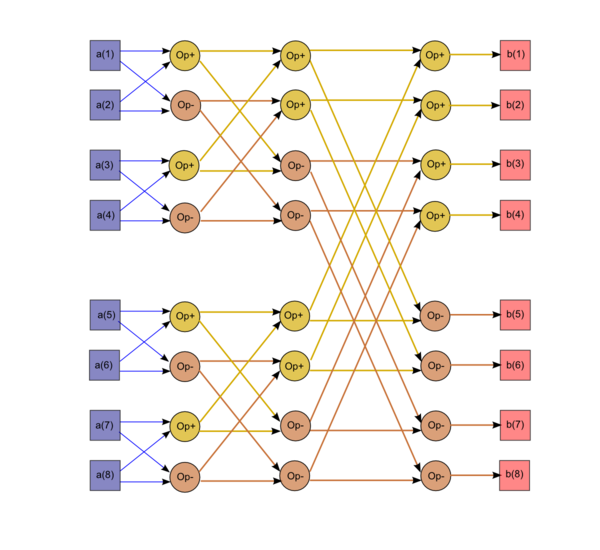
Как видно из рисунка, этот граф не является линейным ни по размерам, ни по формулам для дуг графа. По размерам он линейно-логарифмический, а формулы дуг имеют экспоненциальные компоненты.В элементарной "бабочке" на i-м шаге каждый раз участвует пара элементов массива, у которых запись их номеров, уменьшенных на единицу, в двоичной системе различается только в i-1-м бите.

1.8 Описание ресурса параллелизма алгоритма

Если считать только главные члены выражений, то простой алгоритм Кули-Тьюки имеет критический путь, состоящий из [math]log_{2} n [/math] операций комплексного сложения/вычитания и [math]log_{2} n [/math] операций комплексного умножения. Таким образом, простой алгоритм Кули-Тьюки может быть отнесён к логарифмическому классу по параллельной сложности. По ширине ЯПФ сложность алгоритма линейна.

1.9 Описание входных и выходных данных

Входные данные: вектор [math]a[/math] (элементы [math]a_{i}[/math]).

Объём входных данных: [math]n[/math] .

Выходные данные: вектор [math]b[/math] (элементы [math]b_{i}[/math]).

Объём выходных данных: [math]n[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – логарифмическая.

При этом алгоритм полностью детерминирован.

Заметим, что простой алгоритм Кули-Тьюки не является оптимальным даже для векторов размером степень двойки. Однако здесь мы не рассматриваем другие алгоритмы БПФ.