Poisson equation, solving with DFT, locality
Primary author of this description: Vad.V.Voevodin (section 2).
Contents
1 Links
The basic fragment of the implementation used for obtaining quantitative estimates is given here [1] (the Kernel function).
2 Locality of data and computations
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
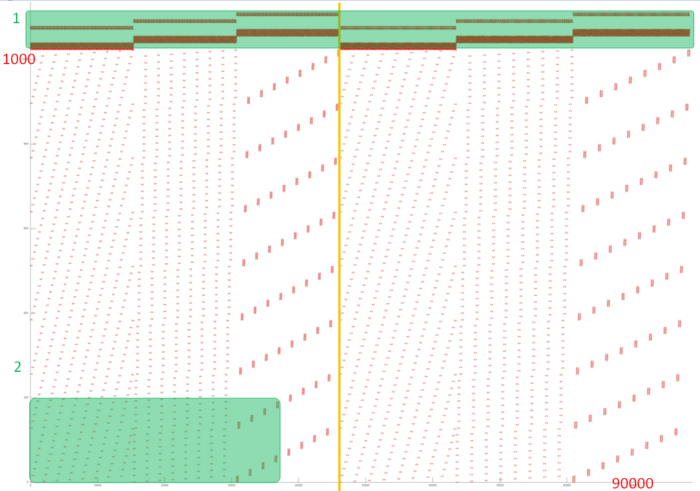
Figure 1 presents the memory access profile for an implementation of the discrete Fourier transform as a method for solving the Poisson equation. This profile includes accesses to several service arrays (fragment 1) and to the main array (fragment 2). One can see that the profile can be split into two virtually identical stages (see the vertical yellow line). On the whole, the overall number of entries is modest (slightly more than 1000 entries); on the other hand, the profile consists of about 100 thousands accesses. It is seen that the density of accesses is higher in the upper part of the profile. This probably indicates a high level of locality; however, the accesses to the main array are fairly scattered. Now consider the locality issue in more detail.
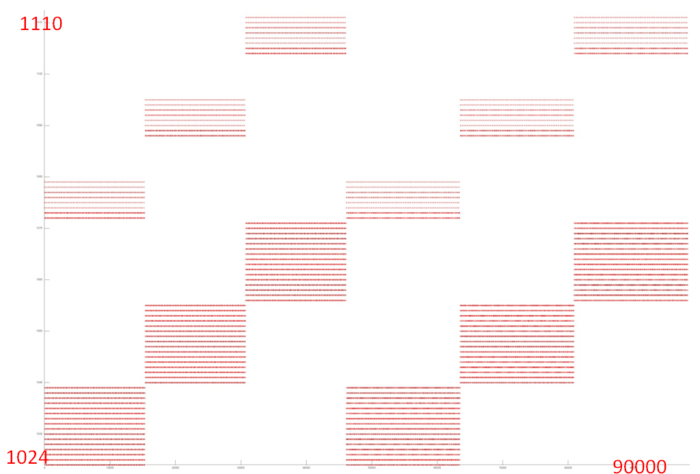
Figure 2 shows fragment 1, which contains all the accesses to the service arrays. From this graph, one cannot say what is the structure of accesses inside the blocks; however, this is not required here. The overall number of referenced addresses is small; there are only about 100 of them used throughout the program. Moreover, they are organized into a block structure, which improves the memory interaction. Thus, one can confidently state, in this case, that the locality (both spatial and temporal) is very high.
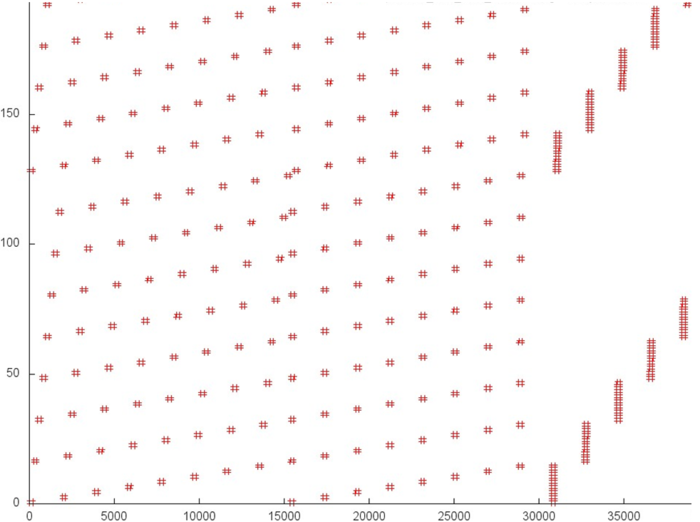
Now, we look at the main array. Figure 3 presents fragment 2 of the general profile shown in fig. 1. One can immediately notice that the graph shows at most several hundreds of accesses, whereas the axis X contains the mark 35000. This means that the vast majority of accesses occurs beyond this fragment; namely, they occur in the service arrays. Thus, on the whole, accesses to the main array occur not very often. An inspection of the original code confirms this conclusion. Indeed, the data stored in the main array are actually only copied to the service arrays. Here, they undergo Fourier transforms, after which the data return to the main array.
According to this fragment, the data that are used in succession are often located close to each other; however, they are rarely used again. Thus, the spatial locality of this fragment is not bad, but its temporal locality is rather low.
Taking into account that the majority of accesses occur to the service arrays and the accesses to the main array have a sufficiently high locality, one can say that, on the whole, the general profile has a high level of locality (both spatial and temporal).
2.1.2 Quantitative estimation of locality
The start-up parameters are described here [2].
The first estimate is produced on the basis of daps, which estimates the number of memory accesses (reading and writing) per second. This characteristic, used for the interaction with memory, is an analog of the flops estimate. It largely estimates the performance of this interaction rather than locality. Nevertheless, this characteristic (in particular, its comparison with the next characteristic cvg) is a good source of information.
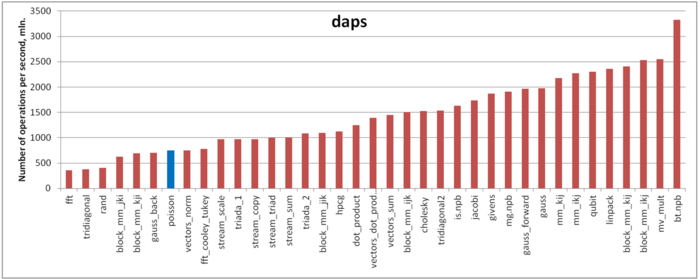
Figure 4 presents the values of daps for implementations of popular algorithms. They are arranged in increasing order (in general, the larger daps, the higher efficiency). Here, we can observe a somewhat unexpected result; namely, despite the assumed high locality, the performance of memory interaction is fairly low.
There seem to be several reasons for this result. The first reason is that the repeated copying of data to and from the service arrays deteriorates both spatial and temporal locality. Second, in the service arrays, the data undergo Fourier transforms based on the Cooley-Tukey algorithm [3]. From this reference, one can see that the performance of memory interaction for the Cooley-Tukey algorithm is very similar to the performance for this Poisson equation solver. The above conclusions about the locality of accesses to the service arrays, where the Fourier transforms are performed, remain also valid for the Cooley-Tukey algorithm; namely, the locality of memory accesses is very high despite a low performance.
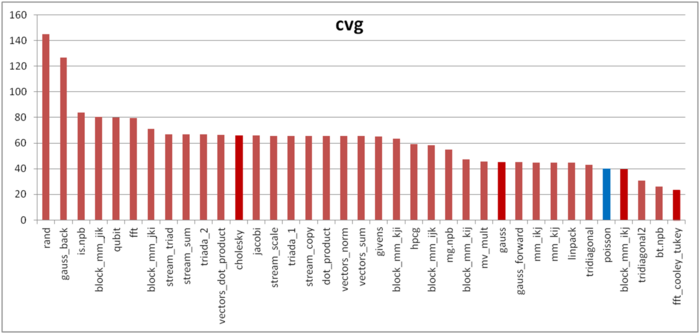
The second characteristic, called cvg, is intended for obtaining a locality estimate that would be more machine independent. It determines how often a program needs to fetch data to the cache memory. Accordingly, smaller values of cvg correspond to less often fetch operations and better locality.
Figure 5 presents the values of cvg for the same set of implementations. They are arranged in decreasing order (in general, the smaller cvg, the higher locality). It can be seen that, similarly to the case of the Cooley-Tukey algorithm, the locality is estimated as very high. The implementation of this algorithm takes up a prominent portion of the general profile for the program under discussion. Consequently, the reasons for this disagreement between locality and performance are identical for both cases (see the detailed discussion of the Cooley-Tukey algorithm).