Difference between revisions of "The serial-parallel summation method"
| [unchecked revision] | [unchecked revision] |
| Line 21: | Line 21: | ||
:<math>S_p = \sum_{j = 1}^q x_{k (p - 1) + j}</math> | :<math>S_p = \sum_{j = 1}^q x_{k (p - 1) + j}</math> | ||
| − | + | When this process is completed, the processors exchange their data, and one of them (or each of them if the result is later needed to all the processors) adds the partial sums in a serial mode. | |
:<math>\sum_{i = 1}^p S_i</math> | :<math>\sum_{i = 1}^p S_i</math> | ||
Revision as of 04:19, 25 October 2017
Primary authors of this description: A.V.Frolov, Vad.V.Voevodin (Section 2.2), A.M.Teplov (раздел Section 2.4)
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 2.1 Implementation peculiarities of the serial algorithm
- 2.2 Locality of data and computations
- 2.3 Possible methods and considerations for parallel implementation of the algorithm
- 2.4 Scalability of the algorithm and its implementations
- 2.5 Dynamic characteristics and efficiency of the algorithm implementation
- 2.6 Conclusions for different classes of computer architecture
- 2.7 Existing implementations of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
The serial-parallel method is used as a substitute for the block implementation of calculating long sequences of associative operations (for instance, mass summations). The method became popular due to the following features: a) it realizes the conversion of single cycles into double ones; b) on serial computers and for certain operations, the method was able to reduce the impact of round-off errors at the results. Here, we describe its version for summing numbers.
1.2 Mathematical description of the algorithm
Input data: one-dimensional array of [math]N[/math] numbers.
Output data: sum of the array's elements.
Formulas of the method: the integer [math]N[/math] is represented as [math]N = (p - 1) k + q[/math], where [math]p[/math] is the number of processors, [math]k = \lceil \frac{N}{p} \rceil[/math], and [math]q = N - k (p - 1)[/math].
Then the [math]i[/math]-th processor (where [math]i \lt p[/math]) calculates, in a serial mode, the sum of array elements with the indices ranging from [math](i - 1) k + 1[/math] to [math]i k[/math].
- [math]S_i = \sum_{j = 1}^k x_{k (i - 1) + j}[/math]
The [math]p[/math]-th processor calculates, in a serial mode, the sum of array elements with the indices ranging from [math](p - 1) k + 1[/math] to [math](p - 1) k + q[/math].
- [math]S_p = \sum_{j = 1}^q x_{k (p - 1) + j}[/math]
When this process is completed, the processors exchange their data, and one of them (or each of them if the result is later needed to all the processors) adds the partial sums in a serial mode.
- [math]\sum_{i = 1}^p S_i[/math]
1.3 Computational kernel of the algorithm
Вычислительное ядро последовательно-параллельного метода суммирования можно составить из множественных (всего [math]p[/math]) вычислений сумм элементов массива:
- [math]S_i = \sum_{j = 1}^k x_{k (i - 1) + j}[/math]
и ещё одного вычисления суммы элементов частичных сумм
- [math]\sum_{i = 1}^p S_i[/math]
1.4 Macro structure of the algorithm
Как уже записано в описании ядра алгоритма, основную часть метода составляют множественные (всего [math]p + 1[/math]) вычисления сумм
- [math]S_i = \sum_{j = 1}^k x_{k (i - 1) + j}[/math]
- [math]\sum_{i = 1}^p S_i[/math]
1.5 Implementation scheme of the serial algorithm
Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов).
1.6 Serial complexity of the algorithm
Для вычисления суммы массива, состоящего из [math]N[/math] элементов, при любых разложениях [math]N[/math] суть алгоритма сводится к простому переставлению скобок в формуле суммирования, и количество операций неизменно и равно [math]N - 1[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.
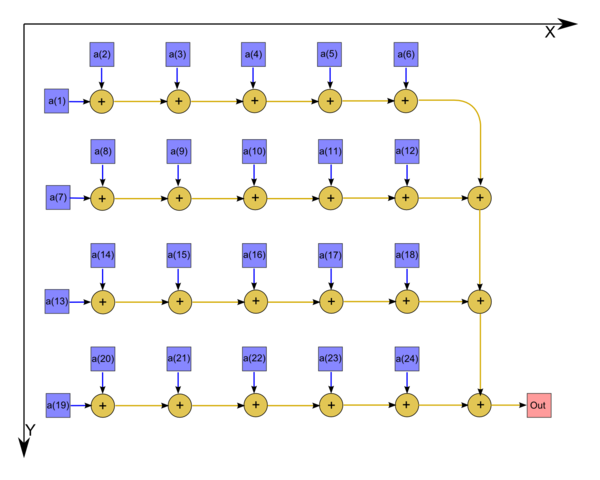
1.7 Information graph
На рис.1 изображён граф алгоритма. В данном случае выполнено суммирование 24 элементов массива.
Интерактивное изображение графа алгоритма без входных и выходных данных для случая суммирования 20 элементов массива
1.8 Parallelization resource of the algorithm
Для суммирования массива порядка [math]n[/math] последовательно-параллельным методом в параллельном варианте требуется последовательно выполнить следующие ярусы:
- [math]k - 1[/math] ярусов суммирования по частям массива ([math]p[/math] ветвей),
- [math]p - 1[/math] ярусов суммирования (одна последовательная ветвь).
Таким образом, в параллельном варианте критический путь алгоритма (и соответствующая ему высота ЯПФ) будет зависеть от произведённого разбиения массива на части. В оптимальном случае ([math]p = \sqrt{n}[/math]) высота ЯПФ будет равна [math]2 \sqrt{n} - 2[/math].
При классификации по высоте ЯПФ, таким образом, последовательно-параллельный метод относится к алгоритмам со сложностью корень квадратный. При классификации по ширине ЯПФ его сложность будет такой же — корень квадратный.
1.9 Input and output data of the algorithm
Входные данные: массив [math]\vec{x}[/math] (элементы [math]x_i[/math]).
Дополнительные ограничения: отсутствуют.
Объём входных данных: [math]N[/math].
Выходные данные: сумма элементов массива.
Объём выходных данных: один скаляр.
1.10 Properties of the algorithm
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является корнем квадратным (отношение линейной к корню квадратному). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных столько же, сколько операций). При этом алгоритм не вполне полностью детерминирован, суммирование может быть проведено в разном порядке. Использование другого порядка выполнения ассоциативных операций может дать, с учётом особенностей входных данных, уменьшение влияния ошибок округления на результат. Дуги информационного графа локальны.
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
В простейшем (без перестановок суммирования) варианте на Фортране можно записать так:
DO I = 1, P
S (I) = X(K*(I-1)+1)
IF (I.LQ.P) THEN
DO J = 2,K
S(I)=S(I)+X(K*(I-1)+J)
END DO
ELSE
DO J = 2,Q
S(I)=S(I)+X(K*(I-1)+J)
END DO
END IF
END DO
SUM = S(1)
DO I = 2, P
SUM = SUM + S(I)
END DO
Можно записать и аналогичные схемы, где суммирование будет проводиться в обратном порядке. Подчеркнём, что граф алгоритма обеих схем — один и тот же!
2.2 Locality of data and computations
2.2.1 Locality of implementation
2.2.1.1 Structure of memory access and a qualitative estimation of locality
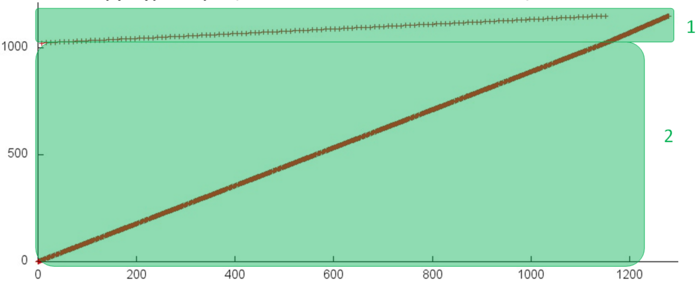
На рис.2 представлен профиль обращений в память для суммирования элементов массива. Данный профиль состоит из обращений к двум массивам, фрагменты для отдельных массивов выделены на рис.2 зеленым цветом. Поскольку мы рассматриваем последовательную реализацию последовательно-параллельного метода суммирования, строение профиля практически никак не зависит от выбранного количества ветвей – будет меняться только число задействованных элементов во фрагменте 1.
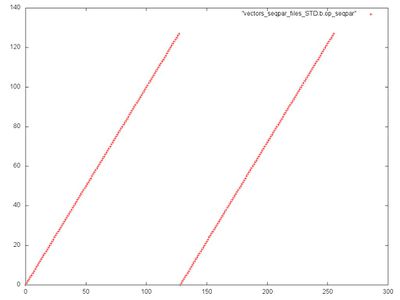
Фрагмент 2 устроен очень просто и представляет собой последовательный перебор всех элементов массива. Фрагмент 1 состоит из двух одинаковых переборов элементов массива, что хорошо видно из рис.3, где данный фрагмент рассмотрен отдельно.
Данные фрагмент характеризуются высокой пространственной локальностью и низкой временной, поскольку практически отсутствуют повторные обращения.
2.2.1.2 Quantitative estimation of locality
Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция KernelOpSeqpar). Условия запуска описаны здесь.
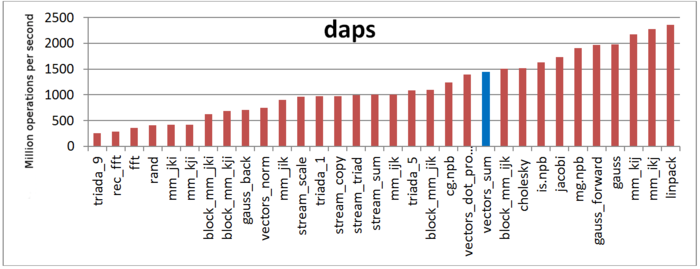
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рис.4 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что значение данной оценки достаточно высоко и близко к последовательно-параллельному скалярному произведению двух векторов, что является закономерным вследствие однотипности структуры выполняемых операций.
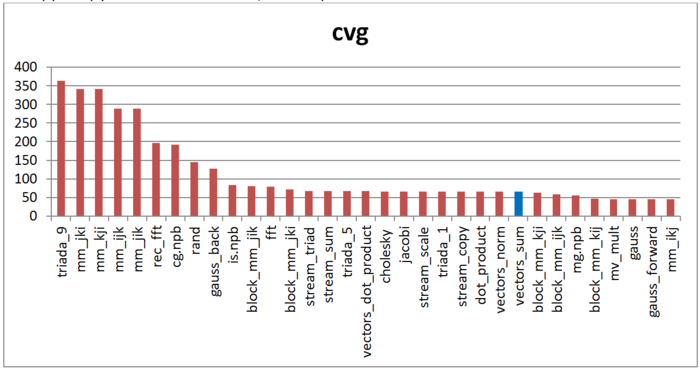
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
На рис.5 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, локальность профиля достаточно высока, что коррелирует со значением оценки daps.
2.3 Possible methods and considerations for parallel implementation of the algorithm
2.4 Scalability of the algorithm and its implementations
2.4.1 Scalability of the algorithm
2.4.2 Scalability of of the algorithm implementation
Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:
- число процессоров [2 : 256]
- размер вектора [80000000:320000000]
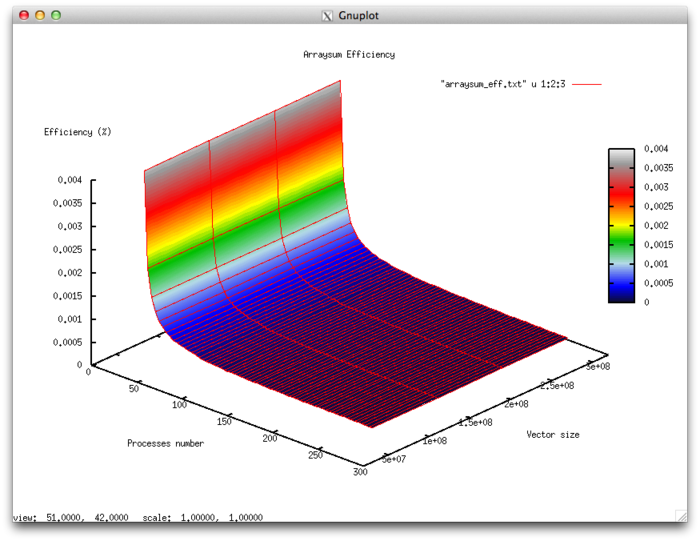
Эффективность выполнения реализации алгоритма
- Минимальная эффективность 0,00004%
- Максимальная эффективность 0,0037%
Оценка масштабируемости
- По числу процессов: -9.432e-07 – при увеличении числа процессов эффективность уменьшается на рассмотренной области изменений параметров запуска, однако, в целом уменьшение не интенсивное. Это объясняется тем, что при увеличении числа процессов сильно возрастает доля накладных расходов на организацию схемы сдваивания сумирования, однако, так как общая эффективность составляет доли процента интенсивность сильная только при переходе от работы процессов в рамках одного физического узла к использованию коммуникационной сети. В остальной области рассмотренных значений параметров запуска эффективность близка к 0 в силу того, что на каждый процесс приходится черезвычайно малая доля вычислений. Больше полезного времени уходит на организацию работы процессов.
- По размеру задачи: 1.881e-06 – при увеличении размера задачи эффективность в целом очень незначительно увеличивается по рассматриваемой области. Это объясняется общим увеличением вычислительной сложности задачи в связи с увеличением размерности. Однако вычислительная сложность алгоритма [math](N-1)[/math]не позволяет существенно увеличить долю времени затрачиваемую на вычисления.
- По двум направлениям: -1.423e-07 – при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений уменьшается, однако интенсивность уменьшения эффективности небольшая. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров несущественная говорит о том, что на поверхности присутствуют области с очень интенсивным изменением эффективности на участке 2-16 процессов, но очень малые по площади. На остальной поверхности изменения эффективности незначительны и находятся на приблизительно одном и том же уровне.
Исследованная реализация алгоритма на языке C
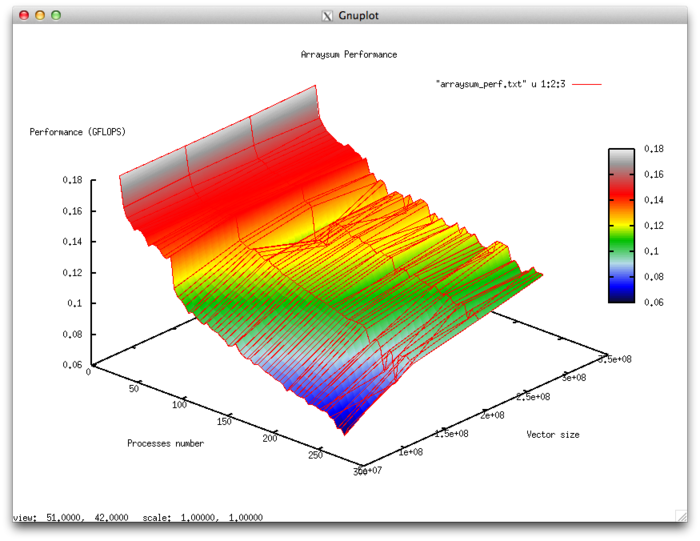
2.5 Dynamic characteristics and efficiency of the algorithm implementation
2.6 Conclusions for different classes of computer architecture
2.7 Existing implementations of the algorithm
В чистом виде алгоритм последовательно-параллельного метода для суммирования массива встречается редко, в основном встречаются его модификации, например для случаев вычисления скалярного произведения (вместо элементов массива будут фигурировать произведения элементов двух массивов), равномерной нормы (вместо элементов массива — их модули) и т. п. В случае вычисления скалярного произведения в одном из частных случаев подобный приём применён в библиотеке BLAS (там одна из размерностей равна 5), но, видимо, не для распараллеливания, а для оптимизации работы с регистрами процессора. Между тем, разбиения массивов на группы для вычислений частных сумм могут быть полезны и для лучшего использования кэша на отдельных узлах.