Участник:Grachovamc/Вычисление кратного интеграла методом Монте - Карло.: различия между версиями
| Строка 16: | Строка 16: | ||
Для определения этой площади можно разбить отрезок, по которому производится интегрирование, на подотрезки, подсчитать площадь под графиком функции на каждом из них и сложить. И если предположить, что в случае функции одной переменной достаточно разбиения на 50 подотрезков и, соответственно, 50 вычислений значений функции, то в случае функции <math>n</math> переменных количество подотрезков и вычислений значений функции возрастает до <math>50^n</math>. При размерности функции больше 10 задача становится очень громоздкой. Поскольку пространства большой размерности встречаются во многих задачах, необходимо иметь метод решения, вычислительная сложность которого бы не столь сильно зависела от размерности. Именно таким свойством обладает метод Монте-Карло. | Для определения этой площади можно разбить отрезок, по которому производится интегрирование, на подотрезки, подсчитать площадь под графиком функции на каждом из них и сложить. И если предположить, что в случае функции одной переменной достаточно разбиения на 50 подотрезков и, соответственно, 50 вычислений значений функции, то в случае функции <math>n</math> переменных количество подотрезков и вычислений значений функции возрастает до <math>50^n</math>. При размерности функции больше 10 задача становится очень громоздкой. Поскольку пространства большой размерности встречаются во многих задачах, необходимо иметь метод решения, вычислительная сложность которого бы не столь сильно зависела от размерности. Именно таким свойством обладает метод Монте-Карло. | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| − | + | Рассмотрим два наиболее распространенных варианта использования метода Монте - Карло для вычисления интегралов. | |
| + | ==== Метод усреднения подынтегральной функции ==== | ||
| + | Рассмотрим интеграл вида | ||
| + | |||
| + | <math>I = \int_a^b \phi(x) dx</math> | ||
| + | |||
| + | Пусть <math>X</math> - случайная величина, равномерно распределенная на отрезке интегрирования <math>[a, b]</math> с плотностью <math>f(x) = \frac{1}{b - a}</math>. Тогда <math>\phi(X)</math> также является случайной величиной, и ее математическое ожидание выражается как | ||
| + | |||
| + | <math>\mathbb{E}\phi(X)=\int\limits_a^b \phi(x)f(x) dx = \frac{1}{b - a}\int\limits_a^b \phi(x) dx</math> | ||
| + | |||
| + | Отсюда | ||
| + | |||
| + | <math>\int_a^b \phi(x) dx = (b - a)\mathbb{E}\phi(X)</math> | ||
| + | |||
| + | Заменив математическое ожидание <math>\mathbb{E}\phi(X)</math> его оценкой – выборочным средним, получим оценку интеграла | ||
| + | |||
| + | <math>\int\limits_{a}^{b}\phi(x)\,dx\approx\frac{b-a}{N}\sum^{N}_{i=1}\phi(x_i)</math>, | ||
| + | |||
| + | где <math>x_i</math> – возможные значения случайной величины <math>X</math>, <math>N</math> – число испытаний. | ||
| + | |||
| + | ==== Геометрический метод ==== | ||
| + | Рассмотрим интеграл вида | ||
| + | |||
| + | <math>I = \int_a^b \phi(x) dx</math>, где подынтегральная функция неотрицательна и ограничена <math>0 \le \phi(x) \le c</math> для любого <math>x \in [a, b]</math>. | ||
| + | |||
| + | Согласно геометрическому определению интеграла для вычисления значения интеграла определим площадь под графиком интегрируемой функции. Для этого применяется следующий стохастический алгоритм: | ||
| + | |||
* функция ограничивается прямоугольником площадью <math>S</math>, в случае <math>n</math> переменных <math>n</math> — мерным параллелепипедом; | * функция ограничивается прямоугольником площадью <math>S</math>, в случае <math>n</math> переменных <math>n</math> — мерным параллелепипедом; | ||
| − | * в данном прямоугольнике случайным образом выбираются координаты <math> | + | * в данном прямоугольнике случайным образом выбираются координаты <math>M</math> точек; |
| − | * определяется число <math> | + | * определяется число <math>m</math> точек, координаты которых попали под график функции; тогда выполняется соотношение <math>\frac{\int\limits_a^b \phi(x) dx}{S} \approx \frac{m}{M}</math> |
| − | * искомая | + | * искомая оценка интеграла равна <math>S\frac{m}{M}</math>. |
| − | |||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| − | Таким образом, вычислительным ядром последовательной реализации данного алгоритма является многократное | + | Таким образом, вычислительным ядром последовательной реализации данного алгоритма является многократное вычисление значения функции в случайной точке и сравнивание полученного значения со . |
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
Согласно описанию вычислительного ядра алгоритма в качестве макровершины можно взять последовательность действий, использующуюся для определения площади под графиком функции и представленную в рамках математического описания алгоритма. | Согласно описанию вычислительного ядра алгоритма в качестве макровершины можно взять последовательность действий, использующуюся для определения площади под графиком функции и представленную в рамках математического описания алгоритма. | ||
| Строка 37: | Строка 62: | ||
[[Файл:1_step.png]] | [[Файл:1_step.png]] | ||
| − | 2. В прямоугольнике случайным образом выбираются координаты <math> | + | 2. В прямоугольнике случайным образом выбираются координаты <math>K</math> точек |
[[Файл:3_step.png]] | [[Файл:3_step.png]] | ||
| Строка 45: | Строка 70: | ||
[[Файл:4_step.png]] | [[Файл:4_step.png]] | ||
| − | 4. Искомая площадь вычисляется согласно формуле <math>S\frac{M}{ | + | 4. Искомая площадь вычисляется согласно формуле <math>S\frac{M}{K}</math> |
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| + | Таким образом, для вычисления определенного интеграла методом Монте - Карло требуется осуществить: | ||
| + | * | ||
=== Информационный граф === | === Информационный граф === | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
Версия 19:14, 22 октября 2017
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод Монте-Карло — общее название группы численных методов, основанных на получении большого числа реализаций стохастического процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Метод Монте-Карло имеет множество различных приложений. Он применяется для решения задач в различных областях математики, физики, химии, биологии, экономики, оптимизации, теории управления и др.
Годом рождения метода Монте-Карло считается 1949 год, когда в свет выходит статья Метрополиса и Улама «Метод Монте-Карло»[1]. Название метода происходит от названия города в княжестве Монако, широко известного своими многочисленными казино, поскольку именно рулетка является одним из самых широко известных генераторов случайных чисел.
Особенностью данного метода является простая структура вычислительного алгоритма. Как правило, составляется программа для осуществления одного случайного испытания, затем это испытание повторяется N раз, причем каждый опыт не зависит от остальных. Для получения итогового значения усредняются результаты всех опытов. Поэтому метод Монте - Карло также иногда называют методом статистических испытаний[2].
Большим преимуществом метода Монте-Карло является то, что он позволяет учесть в модели элемент случайности и сложность реального мира. Кроме того, метод является робастным по отношению к изменению различных параметров, таких как распределение случайной величины.
Рассмотрим использование метода Монте — Карло для задачи вычисления кратных интегралов.
Предположим, требуется взять определенный интеграл от некоторой функции. Его значение будет численно равно площади под графиком данной функции.
Для определения этой площади можно разбить отрезок, по которому производится интегрирование, на подотрезки, подсчитать площадь под графиком функции на каждом из них и сложить. И если предположить, что в случае функции одной переменной достаточно разбиения на 50 подотрезков и, соответственно, 50 вычислений значений функции, то в случае функции [math]n[/math] переменных количество подотрезков и вычислений значений функции возрастает до [math]50^n[/math]. При размерности функции больше 10 задача становится очень громоздкой. Поскольку пространства большой размерности встречаются во многих задачах, необходимо иметь метод решения, вычислительная сложность которого бы не столь сильно зависела от размерности. Именно таким свойством обладает метод Монте-Карло.
1.2 Математическое описание алгоритма
Рассмотрим два наиболее распространенных варианта использования метода Монте - Карло для вычисления интегралов.
1.2.1 Метод усреднения подынтегральной функции
Рассмотрим интеграл вида
[math]I = \int_a^b \phi(x) dx[/math]
Пусть [math]X[/math] - случайная величина, равномерно распределенная на отрезке интегрирования [math][a, b][/math] с плотностью [math]f(x) = \frac{1}{b - a}[/math]. Тогда [math]\phi(X)[/math] также является случайной величиной, и ее математическое ожидание выражается как
[math]\mathbb{E}\phi(X)=\int\limits_a^b \phi(x)f(x) dx = \frac{1}{b - a}\int\limits_a^b \phi(x) dx[/math]
Отсюда
[math]\int_a^b \phi(x) dx = (b - a)\mathbb{E}\phi(X)[/math]
Заменив математическое ожидание [math]\mathbb{E}\phi(X)[/math] его оценкой – выборочным средним, получим оценку интеграла
[math]\int\limits_{a}^{b}\phi(x)\,dx\approx\frac{b-a}{N}\sum^{N}_{i=1}\phi(x_i)[/math],
где [math]x_i[/math] – возможные значения случайной величины [math]X[/math], [math]N[/math] – число испытаний.
1.2.2 Геометрический метод
Рассмотрим интеграл вида
[math]I = \int_a^b \phi(x) dx[/math], где подынтегральная функция неотрицательна и ограничена [math]0 \le \phi(x) \le c[/math] для любого [math]x \in [a, b][/math].
Согласно геометрическому определению интеграла для вычисления значения интеграла определим площадь под графиком интегрируемой функции. Для этого применяется следующий стохастический алгоритм:
- функция ограничивается прямоугольником площадью [math]S[/math], в случае [math]n[/math] переменных [math]n[/math] — мерным параллелепипедом;
- в данном прямоугольнике случайным образом выбираются координаты [math]M[/math] точек;
- определяется число [math]m[/math] точек, координаты которых попали под график функции; тогда выполняется соотношение [math]\frac{\int\limits_a^b \phi(x) dx}{S} \approx \frac{m}{M}[/math]
- искомая оценка интеграла равна [math]S\frac{m}{M}[/math].
1.3 Вычислительное ядро алгоритма
Таким образом, вычислительным ядром последовательной реализации данного алгоритма является многократное вычисление значения функции в случайной точке и сравнивание полученного значения со .
1.4 Макроструктура алгоритма
Согласно описанию вычислительного ядра алгоритма в качестве макровершины можно взять последовательность действий, использующуюся для определения площади под графиком функции и представленную в рамках математического описания алгоритма.
1.5 Схема реализации последовательного алгоритма
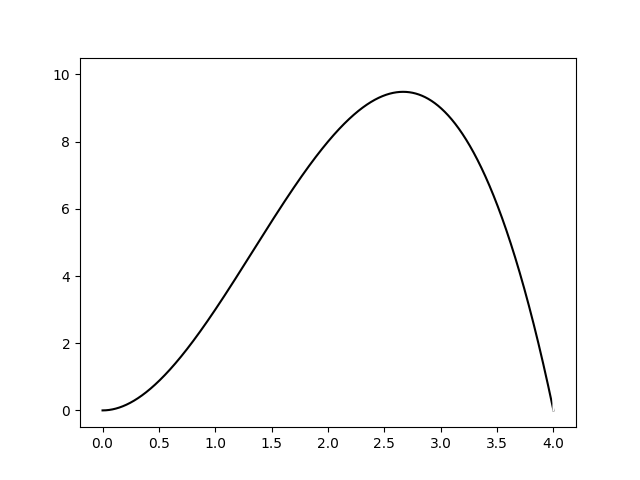
Пусть интегрируемая функция имеет следующий вид
Последовательность исполнения метода следующая. В цикле осуществляется выполнение последовательности действий:
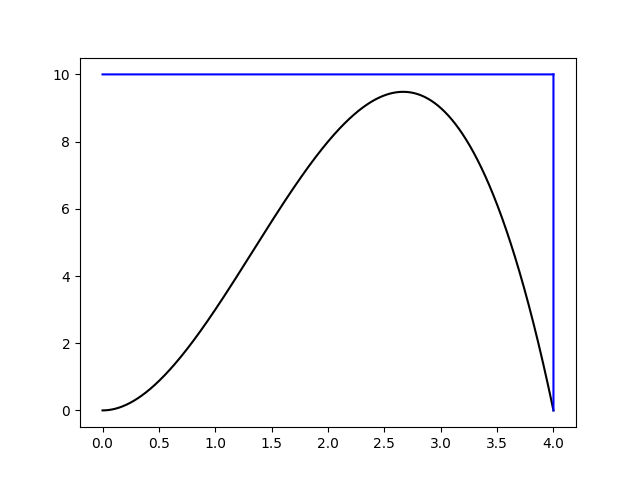
1. Функция ограничивается прямоугольником площадью [math]S[/math]
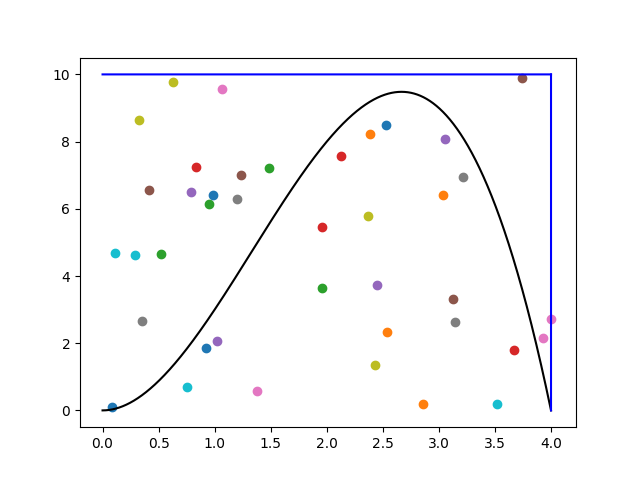
2. В прямоугольнике случайным образом выбираются координаты [math]K[/math] точек
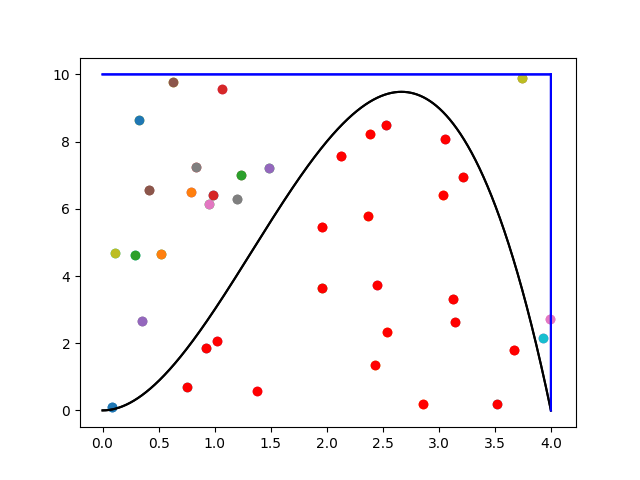
3. Определяется число [math]M[/math] точек, координаты которых попали под график функции
4. Искомая площадь вычисляется согласно формуле [math]S\frac{M}{K}[/math]
1.6 Последовательная сложность алгоритма
Таким образом, для вычисления определенного интеграла методом Монте - Карло требуется осуществить: