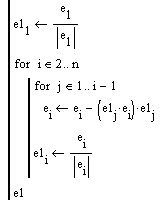Классический метод ортогонализации: различия между версиями
| [досмотренная версия] | [досмотренная версия] |
Frolov (обсуждение | вклад) (Новая страница: «{{algorithm | name = Классическая ортогонализация Грама-Шмидта | serial_complexity = <math>O(N^3)</math> | pf_h…») |
ASA (обсуждение | вклад) |
||
| (не показано 7 промежуточных версий 2 участников) | |||
| Строка 2: | Строка 2: | ||
| name = Классическая ортогонализация Грама-Шмидта | | name = Классическая ортогонализация Грама-Шмидта | ||
| serial_complexity = <math>O(N^3)</math> | | serial_complexity = <math>O(N^3)</math> | ||
| − | | pf_height = <math>O(N)</math> | + | | pf_height = <math>O(N^2)</math> |
| − | | pf_width = <math>O(N | + | | pf_width = <math>O(N)</math> |
| input_data = <math>N^2</math> | | input_data = <math>N^2</math> | ||
| output_data = <math>3N^2/2</math> | | output_data = <math>3N^2/2</math> | ||
}} | }} | ||
| + | |||
| + | Основные авторы описания: [[Участник:DVIN|Инжелевская Дарья Валерьевна]] (свойства и структура алгоритмов), [[Участник:Frolov|А.В.Фролов]](общая редактура текста) | ||
| + | |||
| + | == Свойства и структура алгоритмов == | ||
| + | |||
| + | === Общее описание алгоритма === | ||
| + | |||
| + | Процесс ортогонализации Грама-Шмидта — это один из алгоритмов, в которых на основе множества линейно независимых векторов <math>{\displaystyle \mathbf {a} _{1},\;\ldots ,\;\mathbf {a} _{N}}</math> строится множество ортогональных <math>{\displaystyle \mathbf {b}_{1},\;\ldots ,\;\mathbf {b} _{N}} </math> или ортонормированных векторов <math>{\displaystyle \mathbf {e} _{1},\;\ldots ,\;\mathbf {e}_{N}} </math>, причём так, что каждый вектор <math>{\displaystyle \mathbf {b} _{j}} </math> или <math>{\displaystyle \mathbf {e} _{j}}</math> может быть выражен линейной комбинацией векторов <math>{\displaystyle \mathbf {a} _{1},\;\ldots ,\; \mathbf {a} _{j}}</math>. | ||
| + | |||
| + | === Математическое описание алгоритма === | ||
| + | |||
| + | Пусть имеются линейно независимые векторы <math>\mathbf{a}_1,\;\ldots,\;\mathbf{a}_N</math>. | ||
| + | |||
| + | Если определить оператор проекции следующим образом: <math>\mathbf{proj}_{\mathbf{b}}\,\mathbf{a} = {\langle \mathbf{a}, \mathbf{b} \rangle \over \langle \mathbf{b}, \mathbf{b}\rangle} \mathbf{b} ,</math> | ||
| + | |||
| + | где <math>\langle \mathbf{a}, \mathbf{b} \rangle</math> — скалярное произведение векторов <math>\mathbf{a}</math> и <math>\mathbf{b}</math>, | ||
| + | |||
| + | то классический процесс Грама — Шмидта выполняется следующим образом: | ||
| + | |||
| + | : <math> | ||
| + | {\begin{array}{lclr} | ||
| + | {\mathbf {b}}_{1}&=&{\mathbf {a}}_{1}&(1)\\ | ||
| + | {\mathbf {b}}_{2}&=&{\mathbf {a}}_{2}-{\mathbf {proj}}_{{{\mathbf {b}}_{1}}}\,{\mathbf {a}}_{2}&(2)\\ | ||
| + | {\mathbf {b}}_{3}&=&{\mathbf {a}}_{3}-{\mathbf {proj}}_{{{\mathbf {b}}_{1}}}\,{\mathbf {a}}_{3}-{\mathbf {proj}}_{{{\mathbf {b}}_{2}}}\,{\mathbf {a}}_{3}&(3)\\ | ||
| + | {\mathbf {b}}_{4}&=&{\mathbf {a}}_{4}-{\mathbf {proj}}_{{{\mathbf {b}}_{1}}}\,{\mathbf {a}}_{4}-{\mathbf {proj}}_{{{\mathbf {b}}_{2}}}\,{\mathbf {a}}_{4}-{\mathbf {proj}}_{{{\mathbf {b}}_{3}}}\,{\mathbf {a}}_{4}&(4)\\ | ||
| + | &\vdots &&\\{\mathbf {b}}_{N}&=&{\mathbf {a}}_{N}-\displaystyle \sum _{{j=1}}^{{N-1}}{\mathbf {proj}}_{{{\mathbf {b}}_{j}}}\,{\mathbf {a}}_{N}&(N) | ||
| + | \end{array}} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | На основе каждого вектора <math>\mathbf{b}_j \;(j = 1 \ldots N)</math> может быть получен нормированный вектор: <math>\mathbf{e}_j = {\mathbf{b}_j\over \| \mathbf{b}_j \|_2}</math> (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной). | ||
| + | |||
| + | Результаты процесса Грама — Шмидта: | ||
| + | |||
| + | <math>\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N</math> — система ортогональных векторов либо | ||
| + | |||
| + | <math>\mathbf{e}_1,\;\ldots,\;\mathbf{e}_N</math> — система ортонормированных векторов. | ||
| + | |||
| + | === Вычислительное ядро алгоритма === | ||
| + | |||
| + | Вычислительное ядро последовательной версии метода ортогонализации Грамма-Шмидта можно составить из множественных (всего их <math>\frac{N(N-1)}{2}</math>) вычислений проекций : <math>\mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i}</math> | ||
| + | |||
| + | === Макроструктура алгоритма === | ||
| + | |||
| + | Данный алгоритм использует в качестве составных частей другие, более мелкие. Далее описание будет не в максимально детализированном виде (т.е. на уровне арифметических операций), а только на уровне его макроструктуры. Типичной макрооперацией, часто встречающиеся в алгоритме является оператор проекции векторов. Как записано и в описании ядра алгоритма, основную часть метода ортогонализации Грамма-Шмидта составляют множественные (всего их <math>\frac{N(N-1)}{2}</math>) вычисления оператора проекции. | ||
| + | |||
| + | === Схема реализации последовательного алгоритма === | ||
| + | |||
| + | Следующий алгоритм реализует нормализацию Грамма-Шмидта. Векторы <math>v_1,...,v_k</math> заменяются набором ортонормированных векторов, которые имеют ту же линейную оболочку. | ||
| + | |||
| + | [[File:Gram-Schmidt ortho.png|none|thumb]] | ||
| + | |||
| + | Вычислительная сложность этого <math>2Nk^2</math> операции с плавающей точкой, где N - размерность векторов. | ||
| + | |||
| + | Последовательность исполнения метода следующая: | ||
| + | |||
| + | 1. <math>\mathbf {b}_{1}=\mathbf {a}_{1}</math> | ||
| + | |||
| + | 2. Далее для всех векторов <math>\mathbf {b}_{i}</math> для <math>i=2 ... N</math> производится вычисление по следующей формуле: | ||
| + | <math>{\mathbf {b}}_{i}={\mathbf {a}}_{i}-\displaystyle \sum _{{j=1}}^{{i-1}}{\mathbf {proj}}_{{{\mathbf {b}}_{j}}}\,{\mathbf {a}}_{i}</math>. | ||
| + | |||
| + | В ней на каждом шаге <math>i</math> по очереди вычисляются все <math>{\mathbf {proj}}_{{{\mathbf {b}}_{j}}}\,{\mathbf {a}}_{i}</math> для <math>j=1 ... i-1</math> | ||
| + | |||
| + | ==== Пример реализации на Python ==== | ||
| + | |||
| + | Функция работает для произвольного количества векторов любой размерности. При этом если количество векторов <math>\mathbf{a}_1,\;\ldots,\;\mathbf{a}_N</math> больше их размерности или они линейно зависимы то функция возвращает максимально возможное число линейно независимых векторов <math>\mathbf{b}_1,\;\ldots,\;\mathbf{b}_n</math>, а остальные векторы <math>\mathbf{b}_{n+1},\;\ldots,\;\mathbf{b}_N</math> нулевые. | ||
| + | <source lang="python"> | ||
| + | import random | ||
| + | |||
| + | def GramSchmidt(*a): | ||
| + | k=len(a[0]) | ||
| + | N=len(a); | ||
| + | b = [[0] * k for i in range(N)] | ||
| + | b[0]=a[0] | ||
| + | for i in range(1,N): | ||
| + | sum=a[i] | ||
| + | for j in range(0,i): | ||
| + | scolar_ab=0 | ||
| + | scolar_bb=0 | ||
| + | proj=[i for i in range(k)] | ||
| + | for n in range(k): | ||
| + | scolar_ab+=b[j][n]*a[i][n] | ||
| + | scolar_bb+=b[j][n]*b[j][n] | ||
| + | for n in range(k): | ||
| + | proj[n]=(scolar_ab/scolar_bb)*b[j][n] | ||
| + | for n in range(k): | ||
| + | sum[n]-=proj[n] | ||
| + | b[i]=sum | ||
| + | return b; | ||
| + | |||
| + | l1=[random.randrange(0,10) for i in range(3)] | ||
| + | l2=[random.randrange(0,10) for i in range(3)] | ||
| + | l3=[random.randrange(0,10) for i in range(3)] | ||
| + | print(l1,l2,l3) | ||
| + | print(GramSchmidt(l1,l2,l3)) | ||
| + | </source> | ||
| + | |||
| + | === Последовательная сложность алгоритма === | ||
| + | |||
| + | Для построения ортогонального набора векторов в последовательном варианте требуется: | ||
| + | |||
| + | При k=N: | ||
| + | |||
| + | * <math>\frac{N(N-1)}{2}</math> делений, | ||
| + | |||
| + | * <math>\frac{N(N-1)(3N-1)}{2}</math> сложений (вычитаний), | ||
| + | |||
| + | * <math>\frac{3N^2 (N-1)}{2}</math> умножений. | ||
| + | |||
| + | При k≠N | ||
| + | |||
| + | * <math>\frac{N(N-1)}{2}</math> делений, | ||
| + | |||
| + | * <math>\frac{N(N-1)(3k-1)}{2}</math> сложений (вычитаний), | ||
| + | |||
| + | * <math>\frac{3Nk (N-1)}{2}</math> умножений. | ||
| + | |||
| + | При классификации по последовательной сложности, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам с кубической сложностью. | ||
| + | |||
| + | === Информационный граф === | ||
| + | |||
| + | Опишем граф алгоритма как аналитически, так и в виде рисунка. | ||
| + | |||
| + | Граф алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двух областей. | ||
| + | |||
| + | '''Первая''' группа вершин расположена в двумерной области, соответствующая ей операция <math>\mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i} = {\langle \mathbf{a_i}, \mathbf{b_j} \rangle \over \langle \mathbf{b_j}, \mathbf{b_j}\rangle} \mathbf{b_j} ,</math> . | ||
| + | |||
| + | Естественно введённые координаты области таковы: | ||
| + | |||
| + | i — меняется в диапазоне от 2 до N, принимая все целочисленные значения; | ||
| + | |||
| + | j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения. | ||
| + | |||
| + | Аргументы операции следующие: | ||
| + | |||
| + | <math>a_i</math>: | ||
| + | элементы входных данных, а именно <math>a_i</math>; | ||
| + | |||
| + | <math>b_j</math>: | ||
| + | результат срабатывания операции, соответствующей вершине из второй группы, с координатой j. | ||
| + | |||
| + | '''Вторая''' группа вершин расположена в двухмерной области, соответствующая ей операция <math>a - b</math>. | ||
| + | |||
| + | Естественно введённые координаты области таковы: | ||
| + | |||
| + | i — меняется в диапазоне от 2 до N, принимая все целочисленные значения; | ||
| + | |||
| + | j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения. | ||
| + | |||
| + | Аргументы операции следующие: | ||
| + | |||
| + | a: | ||
| + | |||
| + | j=1 - входные данные <math>a_j</math> | ||
| + | |||
| + | j>1 - результат срабатывания операции, соответствующей вершине из второй группы, с координатой j-1 | ||
| + | |||
| + | b: | ||
| + | |||
| + | результат срабатывания операции, соответствующей вершине из первой группы, с координатой j | ||
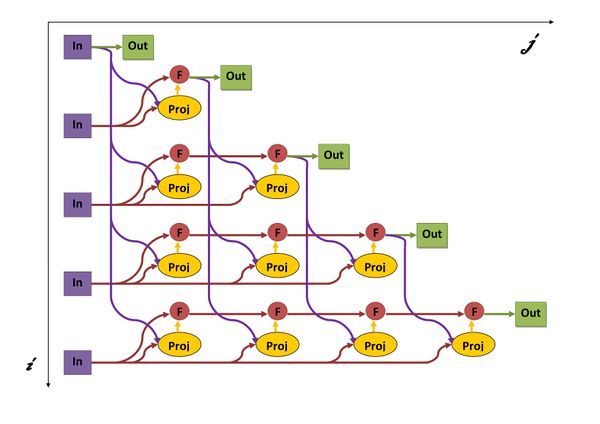
| + | [[Файл:picture00001.jpg|мини|upright=2|centre|frame|Рис. 5. Граф алгоритма с отображением входных и выходных данных. Proj - вычисление оператора проекции, F - операция a-b, In - входные данные, Out - результаты.]] | ||
| + | |||
| + | === Ресурс параллелизма алгоритма === | ||
| + | |||
| + | В параллельном варианте, в отличие от последовательного, можно параллельно производить вычитание соответствующего <math>\mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i}</math> для всех <math>i=j+1..N</math>. Параллельное же вычисление проекций соответствует другому алгоритму. | ||
| + | |||
| + | При классификации по высоте (количество ярусов в ЯПФ ) ЯПФ, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам со сложностью <math>O(N^2)</math>. | ||
| + | |||
| + | При классификации по ширине (максимальное количество вершин в ярусе) ЯПФ его сложность будет <math>O(N)</math>. | ||
| + | |||
| + | === Входные и выходные данные алгоритма === | ||
| + | |||
| + | '''Входные данные''': множества линейно независимых векторов <math>{\displaystyle \mathbf {a} _{1},\;\ldots ,\;\mathbf {a} _{N}}</math>, каждый из которых описывается <math>\mathbf{ a_i= [a^i_1, a^i_2, ..., a^i_k]}</math> . | ||
| + | |||
| + | Дополнительные ограничения: | ||
| + | * вектора <math>{\displaystyle \mathbf {a} _{1},\;\ldots ,\;\mathbf {a} _{N}}</math> линейно независимы, поэтому <math>k \geqslant N</math>. | ||
| + | |||
| + | '''Объём входных данных''': <math>Nk</math> | ||
| + | |||
| + | '''Выходные данные''': множество ортогональных векторов <math>{\displaystyle \mathbf {b} _{1},\;\ldots ,\;\mathbf {b} _{N}} </math>, каждый из которых описывается <math>\mathbf{ b_i= [b^i_1, b^i_2, ..., b^i_k]}</math> . | ||
| + | |||
| + | '''Объём выходных данных''': <math>Nk</math> | ||
| + | |||
| + | === Свойства алгоритма === | ||
| + | |||
| + | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение кубической к квадратичной). | ||
| + | |||
| + | При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, также линейна. | ||
| + | |||
| + | Алгоритм почти полностью детерминирован — единственность результата выполнения гарантирована, однако возможно накопление ошибок округления при использовании классического процесса Грама-Шмидта. | ||
| + | |||
| + | Алгоритм является численно неустойчивым — ошибки округления могут привести к неортогональности полученных векторов. | ||
| + | |||
| + | Процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов. | ||
| + | |||
| + | Кроме того, процесс Грама — Шмидта может применяться к линейно зависимым векторам. В этом случае он выдаёт <math>\mathbf{0}</math> (нулевой вектор) на шаге <math>j</math>, если <math>\mathbf{a}_j</math> является линейной комбинацией векторов <math>\mathbf{a}_1,\;\ldots,\;\mathbf{a}_{j-1}</math>. Если это может случиться, то для сохранения ортогональности выходных векторов и для предотвращения деления на ноль при ортонормировании алгоритм должен делать проверку на нулевые векторы и отбрасывать их. Количество векторов, выдаваемых алгоритмом, будет равно размерности подпространства, порождённого векторами (т.е. количеству линейно независимых векторов, которые можно выделить среди исходных векторов). | ||
| + | |||
| + | Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами ― QR-разложение, что есть частный случай разложения Ивасавы. | ||
| + | |||
| + | == Программная реализация алгоритма == | ||
| + | === Особенности реализации последовательного алгоритма === | ||
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| + | === Результаты прогонов === | ||
| + | === Выводы для классов архитектур === | ||
| + | == Литература == | ||
| + | |||
| + | <references /> | ||
| + | |||
| + | [[Категория:Статьи в работе]] | ||
| + | |||
| + | [[en:Classical orthogonalization method]] | ||
Текущая версия на 08:47, 9 июля 2022
| Классическая ортогонализация Грама-Шмидта | |
| Последовательный алгоритм | |
| Последовательная сложность | O(N^3) |
| Объём входных данных | N^2 |
| Объём выходных данных | 3N^2/2 |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O(N^2) |
| Ширина ярусно-параллельной формы | O(N) |
Основные авторы описания: Инжелевская Дарья Валерьевна (свойства и структура алгоритмов), А.В.Фролов(общая редактура текста)
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Процесс ортогонализации Грама-Шмидта — это один из алгоритмов, в которых на основе множества линейно независимых векторов {\displaystyle \mathbf {a} _{1},\;\ldots ,\;\mathbf {a} _{N}} строится множество ортогональных {\displaystyle \mathbf {b}_{1},\;\ldots ,\;\mathbf {b} _{N}} или ортонормированных векторов {\displaystyle \mathbf {e} _{1},\;\ldots ,\;\mathbf {e}_{N}} , причём так, что каждый вектор {\displaystyle \mathbf {b} _{j}} или {\displaystyle \mathbf {e} _{j}} может быть выражен линейной комбинацией векторов {\displaystyle \mathbf {a} _{1},\;\ldots ,\; \mathbf {a} _{j}}.
1.2 Математическое описание алгоритма
Пусть имеются линейно независимые векторы \mathbf{a}_1,\;\ldots,\;\mathbf{a}_N.
Если определить оператор проекции следующим образом: \mathbf{proj}_{\mathbf{b}}\,\mathbf{a} = {\langle \mathbf{a}, \mathbf{b} \rangle \over \langle \mathbf{b}, \mathbf{b}\rangle} \mathbf{b} ,
где \langle \mathbf{a}, \mathbf{b} \rangle — скалярное произведение векторов \mathbf{a} и \mathbf{b},
то классический процесс Грама — Шмидта выполняется следующим образом:
- {\begin{array}{lclr} {\mathbf {b}}_{1}&=&{\mathbf {a}}_{1}&(1)\\ {\mathbf {b}}_{2}&=&{\mathbf {a}}_{2}-{\mathbf {proj}}_{{{\mathbf {b}}_{1}}}\,{\mathbf {a}}_{2}&(2)\\ {\mathbf {b}}_{3}&=&{\mathbf {a}}_{3}-{\mathbf {proj}}_{{{\mathbf {b}}_{1}}}\,{\mathbf {a}}_{3}-{\mathbf {proj}}_{{{\mathbf {b}}_{2}}}\,{\mathbf {a}}_{3}&(3)\\ {\mathbf {b}}_{4}&=&{\mathbf {a}}_{4}-{\mathbf {proj}}_{{{\mathbf {b}}_{1}}}\,{\mathbf {a}}_{4}-{\mathbf {proj}}_{{{\mathbf {b}}_{2}}}\,{\mathbf {a}}_{4}-{\mathbf {proj}}_{{{\mathbf {b}}_{3}}}\,{\mathbf {a}}_{4}&(4)\\ &\vdots &&\\{\mathbf {b}}_{N}&=&{\mathbf {a}}_{N}-\displaystyle \sum _{{j=1}}^{{N-1}}{\mathbf {proj}}_{{{\mathbf {b}}_{j}}}\,{\mathbf {a}}_{N}&(N) \end{array}}
На основе каждого вектора \mathbf{b}_j \;(j = 1 \ldots N) может быть получен нормированный вектор: \mathbf{e}_j = {\mathbf{b}_j\over \| \mathbf{b}_j \|_2} (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).
Результаты процесса Грама — Шмидта:
\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N — система ортогональных векторов либо
\mathbf{e}_1,\;\ldots,\;\mathbf{e}_N — система ортонормированных векторов.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро последовательной версии метода ортогонализации Грамма-Шмидта можно составить из множественных (всего их \frac{N(N-1)}{2}) вычислений проекций : \mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i}
1.4 Макроструктура алгоритма
Данный алгоритм использует в качестве составных частей другие, более мелкие. Далее описание будет не в максимально детализированном виде (т.е. на уровне арифметических операций), а только на уровне его макроструктуры. Типичной макрооперацией, часто встречающиеся в алгоритме является оператор проекции векторов. Как записано и в описании ядра алгоритма, основную часть метода ортогонализации Грамма-Шмидта составляют множественные (всего их \frac{N(N-1)}{2}) вычисления оператора проекции.
1.5 Схема реализации последовательного алгоритма
Следующий алгоритм реализует нормализацию Грамма-Шмидта. Векторы v_1,...,v_k заменяются набором ортонормированных векторов, которые имеют ту же линейную оболочку.
Вычислительная сложность этого 2Nk^2 операции с плавающей точкой, где N - размерность векторов.
Последовательность исполнения метода следующая:
1. \mathbf {b}_{1}=\mathbf {a}_{1}
2. Далее для всех векторов \mathbf {b}_{i} для i=2 ... N производится вычисление по следующей формуле: {\mathbf {b}}_{i}={\mathbf {a}}_{i}-\displaystyle \sum _{{j=1}}^{{i-1}}{\mathbf {proj}}_{{{\mathbf {b}}_{j}}}\,{\mathbf {a}}_{i}.
В ней на каждом шаге i по очереди вычисляются все {\mathbf {proj}}_{{{\mathbf {b}}_{j}}}\,{\mathbf {a}}_{i} для j=1 ... i-1
1.5.1 Пример реализации на Python
Функция работает для произвольного количества векторов любой размерности. При этом если количество векторов \mathbf{a}_1,\;\ldots,\;\mathbf{a}_N больше их размерности или они линейно зависимы то функция возвращает максимально возможное число линейно независимых векторов \mathbf{b}_1,\;\ldots,\;\mathbf{b}_n, а остальные векторы \mathbf{b}_{n+1},\;\ldots,\;\mathbf{b}_N нулевые.
import random
def GramSchmidt(*a):
k=len(a[0])
N=len(a);
b = [[0] * k for i in range(N)]
b[0]=a[0]
for i in range(1,N):
sum=a[i]
for j in range(0,i):
scolar_ab=0
scolar_bb=0
proj=[i for i in range(k)]
for n in range(k):
scolar_ab+=b[j][n]*a[i][n]
scolar_bb+=b[j][n]*b[j][n]
for n in range(k):
proj[n]=(scolar_ab/scolar_bb)*b[j][n]
for n in range(k):
sum[n]-=proj[n]
b[i]=sum
return b;
l1=[random.randrange(0,10) for i in range(3)]
l2=[random.randrange(0,10) for i in range(3)]
l3=[random.randrange(0,10) for i in range(3)]
print(l1,l2,l3)
print(GramSchmidt(l1,l2,l3))
1.6 Последовательная сложность алгоритма
Для построения ортогонального набора векторов в последовательном варианте требуется:
При k=N:
- \frac{N(N-1)}{2} делений,
- \frac{N(N-1)(3N-1)}{2} сложений (вычитаний),
- \frac{3N^2 (N-1)}{2} умножений.
При k≠N
- \frac{N(N-1)}{2} делений,
- \frac{N(N-1)(3k-1)}{2} сложений (вычитаний),
- \frac{3Nk (N-1)}{2} умножений.
При классификации по последовательной сложности, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам с кубической сложностью.
1.7 Информационный граф
Опишем граф алгоритма как аналитически, так и в виде рисунка.
Граф алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двух областей.
Первая группа вершин расположена в двумерной области, соответствующая ей операция \mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i} = {\langle \mathbf{a_i}, \mathbf{b_j} \rangle \over \langle \mathbf{b_j}, \mathbf{b_j}\rangle} \mathbf{b_j} , .
Естественно введённые координаты области таковы:
i — меняется в диапазоне от 2 до N, принимая все целочисленные значения;
j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения.
Аргументы операции следующие:
a_i: элементы входных данных, а именно a_i;
b_j: результат срабатывания операции, соответствующей вершине из второй группы, с координатой j.
Вторая группа вершин расположена в двухмерной области, соответствующая ей операция a - b.
Естественно введённые координаты области таковы:
i — меняется в диапазоне от 2 до N, принимая все целочисленные значения;
j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения.
Аргументы операции следующие:
a:
j=1 - входные данные a_j
j>1 - результат срабатывания операции, соответствующей вершине из второй группы, с координатой j-1
b:
результат срабатывания операции, соответствующей вершине из первой группы, с координатой j
1.8 Ресурс параллелизма алгоритма
В параллельном варианте, в отличие от последовательного, можно параллельно производить вычитание соответствующего \mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i} для всех i=j+1..N. Параллельное же вычисление проекций соответствует другому алгоритму.
При классификации по высоте (количество ярусов в ЯПФ ) ЯПФ, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам со сложностью O(N^2).
При классификации по ширине (максимальное количество вершин в ярусе) ЯПФ его сложность будет O(N).
1.9 Входные и выходные данные алгоритма
Входные данные: множества линейно независимых векторов {\displaystyle \mathbf {a} _{1},\;\ldots ,\;\mathbf {a} _{N}}, каждый из которых описывается \mathbf{ a_i= [a^i_1, a^i_2, ..., a^i_k]} .
Дополнительные ограничения:
- вектора {\displaystyle \mathbf {a} _{1},\;\ldots ,\;\mathbf {a} _{N}} линейно независимы, поэтому k \geqslant N.
Объём входных данных: Nk
Выходные данные: множество ортогональных векторов {\displaystyle \mathbf {b} _{1},\;\ldots ,\;\mathbf {b} _{N}} , каждый из которых описывается \mathbf{ b_i= [b^i_1, b^i_2, ..., b^i_k]} .
Объём выходных данных: Nk
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение кубической к квадратичной).
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, также линейна.
Алгоритм почти полностью детерминирован — единственность результата выполнения гарантирована, однако возможно накопление ошибок округления при использовании классического процесса Грама-Шмидта.
Алгоритм является численно неустойчивым — ошибки округления могут привести к неортогональности полученных векторов.
Процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов.
Кроме того, процесс Грама — Шмидта может применяться к линейно зависимым векторам. В этом случае он выдаёт \mathbf{0} (нулевой вектор) на шаге j, если \mathbf{a}_j является линейной комбинацией векторов \mathbf{a}_1,\;\ldots,\;\mathbf{a}_{j-1}. Если это может случиться, то для сохранения ортогональности выходных векторов и для предотвращения деления на ноль при ортонормировании алгоритм должен делать проверку на нулевые векторы и отбрасывать их. Количество векторов, выдаваемых алгоритмом, будет равно размерности подпространства, порождённого векторами (т.е. количеству линейно независимых векторов, которые можно выделить среди исходных векторов).
Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами ― QR-разложение, что есть частный случай разложения Ивасавы.