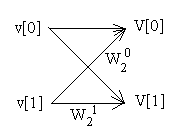Участник:Ivanov.kir.m/Быстрое дискретное преобразование Фурье

Алгоритм Кули-Тьюки одномерного преобразования Фурье для действительных чисел
Последовательный алгоритм
Последовательная сложность	[math]O (n \log n)[/math]
Объём входных данных	[math]n[/math] действительных чисел
Объём выходных данных	[math]\lfloor n/2 \rfloor+1[/math] комплексных чисел
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O (\log n)[/math]
Ширина ярусно-параллельной формы	[math]n[/math]

Быстрое преобразование Фурье (БПФ, FFT) — алгоритм быстрого  вычисления дискретного преобразования Фурье (ДПФ). То есть, алгоритм вычисления за количество действий, меньшее чем [math]O(N^{2})[/math], требуемых для прямого (по формуле) вычисления ДПФ. Иногда под БПФ понимается один из быстрых алгоритмов, называемый алгоритмом прореживания по частоте/времени или алгоритмом по основанию 2, имеющий сложность [math]O(N\log(N))[/math]. Cуществует несколько различных алгоритмов для вычисления ДПФ считающимся быстрым преобразование Фурье:

• Алгоритм Кули-Тьюки [1]
• Алгоритм Гуда-Томаса [2]
• Алгоритм Бруна [3]
• Алгоритм Блюштейна [4]

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Одним из вариантов быстрого преобразования Фурье для вектора действительных чисел с размерностью равной степени двойки является алгоритм Кули-Тьюки. Отличительной особенностью данного алгоритма является то, что он обходится без использования специфических приемов, использующихся именно для степеней четверки, восьмерки и т.п. Однако благодаря тому, что на вход данному алгоритму подается вектор чисто вещественных чисел, выходной вектор удовлетворяет эрмитовой избыточности (Hermitian redundancy) , т.е. [math]out[i][/math] является сопряженным с [math]out[n-i][/math]. Это обстоятельство позволяет достичь роста скорости и снижения затрат памяти примерно в 2 раза по сравнению с комплексным аналогом алгоритма.

1.2 Математическое описание алгоритма

Входные данные: вектор действительных чисел [math]a = (a_1,a_2,...,a_n)[/math].

Выходные данные: вектор комплексных чисел [math]b = (b_1,b_2,...,b_{\lfloor n/2 \rfloor+1})[/math].

Замечание: В простейшем случае алгоритм Кули-Тьюки применяется к векторам размерности степени двойки, поэтому на практике вектора иной размерности часто дополнять до ближайшей степени двойки. Такой подход делает алгоритм Кули-Тьюки не самым эффективным алгоритмом БПФ, поскольку дополнение до степени двойки может сильно усложнить задачу.

1.3 Рекурсивное описание

Алгоритм:

1. Входной вектор [math]a = (a_1,a_2,...,a_n)[/math] преобразуется в матрицу [math]A[/math] размера [math]n_1 \times n_2 [/math], где [math]n=n_1 \cdot n_2[/math] и [math]n_1 \lt n_2[/math]

[math] A = \begin{pmatrix} a_1 & a_2 & \cdots & a_{n_1} \\ a_{n_1+1} & a_{n_1} & \cdots & a_{2n_1} \\ \vdots & \vdots & \ddots & \vdots \\ a_{(n2-1)\cdot n1+1} & a_{(n2-1)\cdot n1+1} & \cdots & a_{n2\cdot n1} \end{pmatrix} [/math]

1. К каждой строке полученной матрицы применяется дискретное преобразование Фурье порядка [math]n_1[/math]
2. Каждый элемент полученный после применения ДПФ умножается на поворотные множители [math]exp (2 \pi i(m-1)(j-1)/n)[/math], где [math]m[/math] - номер строки, а [math]j[/math] - номер столбца
3. Полученная после шагов 1-3 матрица [math]A[/math] транспонируется
4. К каждой строке матрицы [math]A^T[/math] применяется ДПФ порядка [math]n_2[/math]

Замечание: Как правило все поворотные множители вычисляются заранее и хранятся в специальном массиве.

1.4 Вычислительное ядро алгоритма

В случае размерности входа равной степени двойки, вычислительным ядром алгоритма является, так называемая, "бабочка". В простейшем случае "бабочка" представляет из себя двухточечное преобразование. Рассмотрим этот случай:

На вход алгоритму подается двухэлементный вектор ‒ [math] v = (v[0], v[1]) [/math]. Тогда для вычисления будут происходить по следующим формулам:

[math]V[0] = W_2^0 v[0] + W_2^0 v[1] = v[0] + W_2^0 v[1] [/math]

[math]V[1] = W_2^0 v[0] + W_2^1 v[1] = v[0] + W_2^1 v[1] [/math]

Данный процесс удобно изобразить с помощью следующей схемы:

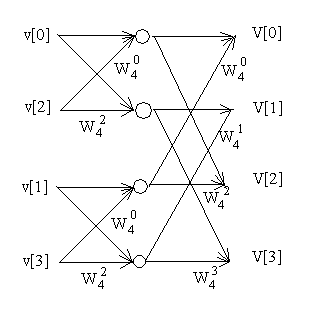
Для 4-х элеметного вектора [math]v=(v[0],v[1],v[2],v[3])[/math], алгоритм строится похожим образом. Сначала создаются простейшие "бабочки", а потом их результаты соединяются с противоположеной "бабочкой":

[math]V[0]=v[0]+W_2^0 v[2]+W_4^0(v[1]+W_2^0 v[3])[/math]

[math]V[1]=v[0]-W_2^0 v[2]+W_4^1(v[1]-W_2^0 v[3])[/math]

[math]V[2]=v[0]+W_2^0 v[2]-W_4^0(v[1]+W_2^0 v[3])[/math]

[math]V[3]=v[0]-W_2^0 v[2]-W_4^1(v[1]-W_2^0 v[3])[/math]

Схема в таком случае будет выглядеть следующим образом:

Для случая, когда вход не является степенью двойки, "бабочки" будут "несимментричными", но в остальном вычисления будут проходить схожим образом.

3 Литература

[1] Википедия [Электронный ресурс]. Тема: Быстрое преобразование Фурье – Электрон. дан. – URL Быстрое преобразование Фурье (дата обращения 17.09.2016)