Сумма вектора и произведения матрицы на другой вектор, вещественная версия, последовательный вариант, плотная матрица: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 37: | Строка 37: | ||
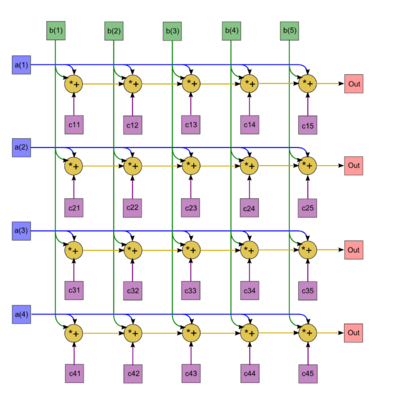
Опишем граф алгоритма в виде рисунка. Пример приведён для <math>m = 4</math>, <math>n = 7</math>. Вершине графа соответствует составная операция умножения двух чисел с последующим сложением с третьим числом. | Опишем граф алгоритма в виде рисунка. Пример приведён для <math>m = 4</math>, <math>n = 7</math>. Вершине графа соответствует составная операция умножения двух чисел с последующим сложением с третьим числом. | ||
| − | [[file:matrix-vector product plus vector (dense matrix).png|center|thumb|400px]] | + | [[file:matrix-vector product plus vector (dense matrix).png|center|thumb|400px|Сумма вектора и произведения матрицы на вектор с отображением только выходных данных]] |
| − | [[file:matrix-vector product plus vector (dense matrix) in_out.png|center|thumb|400px]] | + | [[file:matrix-vector product plus vector (dense matrix) in_out.png|center|thumb|400px|Сумма вектора и произведения матрицы на вектор с отображением входных и выходных данных]] |
=== Описание ресурса параллелизма алгоритма === | === Описание ресурса параллелизма алгоритма === | ||
Текущая версия на 19:01, 15 октября 2014
Содержание
- 1 Описание свойств и структуры алгоритма
- 1.1 Словесное описание алгоритма
- 1.2 Математическое описание
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Описание схемы реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Описание входных и выходных данных
- 1.10 Свойства алгоритма
- 2 Программная реализация
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Описание локальности данных и вычислений
- 2.3 Возможные способы и особенности реализации параллельного алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
1 Описание свойств и структуры алгоритма
1.1 Словесное описание алгоритма
Сумма вектора и произведения матрицы на другой вектор используется в качестве одной из базовых операций в широком круге методов. При этом сумма вектора и произведения матрицы на другой вектор используется как в версии для собственно векторов (одномерных массивов размеров 

1.2 Математическое описание
Исходные данные: два одномерных массива 
Вычисляемые данные: сумма попарных произведений элементов массива.
Формулы метода: для векторов 





для всех 


При этом в последовательном варианте используется последовательный порядок суммирования (обычно от меньших индексов к большим). Существуют и другие способы вычисления искомой суммы, но здесь мы их рассматривать не будем.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро состоит из набора сумм элементов одного вектора и скалярных произведений другого на столбцы матрицы.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть вычисления алгоритма массовый последовательный набор сумм скалярных произведений одного вектора и столбцов матрицы с элементами одного из векторов.
1.5 Описание схемы реализации последовательного алгоритма
Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов), при этом суммировать начинают сразу с элементом вектора 

1.6 Последовательная сложность алгоритма
Для вычисления скалярного сумма вектора и произведения матрицы, количество операций умножения неизменно и равно 



1.7 Информационный граф
Опишем граф алгоритма в виде рисунка. Пример приведён для 





1.8 Описание ресурса параллелизма алгоритма
Последовательный вариант вычисления суммы вектора и произведения матрицы на другой вектор, имеет ресурс параллелизма степени 


1.9 Описание входных и выходных данных
Входные данные: массивы 











Дополнительные ограничения: отсутствуют.
Объём входных данных: 





Выходные данные: сумма произведения матрицы 




Объём выходных данных: 
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, равно 
2 Программная реализация
2.1 Особенности реализации последовательного алгоритма
В простейшем варианте на Фортране можно записать так:
DO I = 1, M
DO J = 1, N
B(I) = B(I) + A(I,J)* X(J)
END DO
END DO
2.2 Описание локальности данных и вычислений
2.2.1 Описание локальности алгоритма
2.2.2 Описание локальности реализации алгоритма
2.2.2.1 Описание структуры обращений в память и качественная оценка локальности
2.2.2.2 Количественная оценка локальности
2.2.2.3 Анализ на основе теста Apex-Map
2.3 Возможные способы и особенности реализации параллельного алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Описание масштабируемости алгоритма
2.4.2 Описание масштабируемости реализации алгоритма
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Помимо выписанных выше простейших реализаций, существуют более сложные коды, реализующие тот же алгоритм. Это объясняется тем, что порой чисто программистскими приёмами оптимизируют работу с регистрами, с кэшем и т. п. В частности, даже в Линпаке есть разные реализации кода. Большинство их сводится к сведению одинарного цикла длиной