Участник:Бугаков Юрий/Построение матрицы Адамара произвольного размера: различия между версиями
м (Lineprinter переименовал страницу Обсуждение:Участники: Бугаков Юрий, Кужамалиев Ернур/Построение матрицы Адамара произвольного размера в…) |
|||
| (не показано 127 промежуточных версий 1 участника) | |||
| Строка 5: | Строка 5: | ||
| − | Важную роль в алгебре и комбинаторике играют матрицы Адамара, которые впервые были введены в математический обиход в конце прошлого века одним из крупнейших французских математиков Жаком Адамаром (1865-1963). Их применение в науке и технике посвящены тысячи публикаций. Они предоставляют эффективные возможности для организации хранения, обработки и передачи информации. | + | Важную роль в алгебре и комбинаторике играют матрицы Адамара, которые впервые были введены в математический обиход в конце прошлого века одним из крупнейших французских математиков [https://ru.wikipedia.org/wiki/%D0%90%D0%B4%D0%B0%D0%BC%D0%B0%D1%80,_%D0%96%D0%B0%D0%BA Жаком Адамаром (1865-1963)]. Их применение в науке и технике посвящены тысячи публикаций. Они предоставляют эффективные возможности для организации хранения, обработки и передачи информации. |
Квадратная матрица Н порядка ''m'' с элементами ±1 называется матрицей Адамара, если выполняется условие | Квадратная матрица Н порядка ''m'' с элементами ±1 называется матрицей Адамара, если выполняется условие | ||
| Строка 11: | Строка 11: | ||
:<math> H_m\,H_m^T = m\,E_m </math> | :<math> H_m\,H_m^T = m\,E_m </math> | ||
| − | Нетрудно заметить, что различные строки матрицы Адамара попарно ортогональны. Также, можно увидеть из определения, что m четно и | + | Нетрудно заметить, что различные строки матрицы Адамара попарно ортогональны [1]. Также, можно увидеть из определения, что m четно и |
:<math> | :<math> | ||
H_{2m} = | H_{2m} = | ||
| Строка 21: | Строка 21: | ||
С матрицами Адамара связан ряд нерешенных проблем, одна из которых состоит в следующем. Мы уже видели, что порядок ''m'' матрицы Адамара при ''m'' ≥ 3 может быть лишь четным. Более того, при ''m'' ≥ 4 порядок обязан делиться на 4. До сих пор остается открытым вопрос: для любого ли ''m'', кратного 4, существует матрица Адамара порядка m? Неизвестно, в частности, существует ли матрица Адамара порядка 268 (это наименьший порядок, кратный 4, для которого матрица Адамара еще не построена). | С матрицами Адамара связан ряд нерешенных проблем, одна из которых состоит в следующем. Мы уже видели, что порядок ''m'' матрицы Адамара при ''m'' ≥ 3 может быть лишь четным. Более того, при ''m'' ≥ 4 порядок обязан делиться на 4. До сих пор остается открытым вопрос: для любого ли ''m'', кратного 4, существует матрица Адамара порядка m? Неизвестно, в частности, существует ли матрица Адамара порядка 268 (это наименьший порядок, кратный 4, для которого матрица Адамара еще не построена). | ||
| − | Часто матрицу Адамара нормализуют и рассматривают | + | Часто матрицу Адамара нормализуют и рассматривают размерности степени 2 (например [2],[3] и [4]). В дальнейшем будем рассматривать только такие случаи. Переопределим матрицу Адамара следующим образом: |
| − | Матрица Адамара ''H''<sub>''n''</sub> - это матрица размера 2<sup>''n''</sup> × 2<sup>''n''</sup>, для которой справедливо равенство | + | '''Матрица Адамара ''H''<sub>''n''</sub> - это матрица размера 2<sup>''n''</sup> × 2<sup>''n''</sup>, для которой справедливо равенство''' |
| − | :<math>H_n = H_{1} \otimes H_{n-1}</math> | + | :<math>H_n = H_{1} \otimes H_{n-1}</math>, |
:<math>\begin{align} | :<math>\begin{align} | ||
| Строка 33: | Строка 33: | ||
1 & -1 | 1 & -1 | ||
\end{array}\end{pmatrix} | \end{array}\end{pmatrix} | ||
| − | \end{align}</math> | + | \end{align}</math>, |
| − | где <math> \otimes </math> представляет собой тензорное произведение. | + | '''где <math> \otimes </math> представляет собой [https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BD%D0%B7%D0%BE%D1%80%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5 тензорное произведение].''' |
Представим некоторые частные примеры матриц Адамара: | Представим некоторые частные примеры матриц Адамара: | ||
| − | :<math> | + | |
| − | + | :<math> | |
| + | H_0 = +1, | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
H_1 = \frac{1}{\sqrt2} | H_1 = \frac{1}{\sqrt2} | ||
| − | + | \begin{pmatrix}\begin{array}{rr} | |
1 & 1\\ | 1 & 1\\ | ||
1 & -1 | 1 & -1 | ||
\end{array}\end{pmatrix} | \end{array}\end{pmatrix} | ||
| − | + | </math>, | |
| − | :<math> | + | |
| + | :<math> | ||
H_2 = \frac{1}{2} | H_2 = \frac{1}{2} | ||
| − | + | \begin{pmatrix}\begin{array}{rrrr} | |
1 & 1 & 1 & 1\\ | 1 & 1 & 1 & 1\\ | ||
1 & -1 & 1 & -1\\ | 1 & -1 & 1 & -1\\ | ||
1 & 1 & -1 & -1\\ | 1 & 1 & -1 & -1\\ | ||
1 & -1 & -1 & 1 | 1 & -1 & -1 & 1 | ||
| − | + | \end{array}\end{pmatrix} | |
| + | </math>, | ||
| + | |||
| + | :<math> | ||
H_3 = \frac{1}{2^{\frac{3}{2}}} | H_3 = \frac{1}{2^{\frac{3}{2}}} | ||
| − | + | \begin{pmatrix}\begin{array}{rrrrrrrr} | |
| − | 1 & 1 & 1 & 1 & | + | 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ |
| − | 1 & -1 & 1 & -1 & | + | 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\ |
| − | 1 & 1 & -1 & -1 & | + | 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1\\ |
| − | 1 & -1 & -1 & 1 & | + | 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1\\ |
| − | 1 & 1 & 1 & | + | 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1\\ |
| − | 1 & -1 & 1 & | + | 1 & -1 & 1 & 1 & -1 & 1 & -1 & 1\\ |
| − | 1 & 1 & -1 & | + | 1 & 1 & -1 & 1 & -1 & -1 & 1 & 1\\ |
| − | 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 | + | 1 & -1 & -1 & -1 & -1 & 1 & 1 & -1\\ |
| − | + | \end{array}\end{pmatrix} | |
| − | + | </math>. | |
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| − | Основой алгоритма является тот факт, что любую матрицу Адамара <math>H_n</math>, размерностью | + | Основой алгоритма является тот факт, что любую матрицу Адамара <math>H_n</math>, размерностью <math>2^n\times 2^n</math> можно вычислить поэлементно ([3], [4]): |
:<math>h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}</math>, | :<math>h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}</math>, | ||
| − | где ''k''<sub>''j''</sub> и ''l''<sub>''j''</sub> коэффициенты двоичного разложения чисел ''k'' и ''l'' (1 или 0) | + | где ''k''<sub>''j''</sub> и ''l''<sub>''j''</sub> коэффициенты двоичного разложения чисел ''k'' и ''l'' (1 или 0): |
| − | : <math>k = \sum^{ | + | : <math>k = \sum^{n}_{i=0} {k_i 2^i} = k_{n} 2^{n} + k_{n-1} 2^{n-1} + \cdots + k_1 2 + k_0</math> |
и | и | ||
| − | : <math>l = \sum^{ | + | : <math>l = \sum^{n}_{i=0} {l_i 2^i} = l_{n} 2^{n} + l_{n-1} 2^{n-1} + \cdots + l_1 2 + l_0</math>. |
| + | |||
| + | Помимо этой формулы чаще всего используется заполнение по определению. В связи с трудностями распараллеливания и постоянного выделения памяти при каждом шаге рекурсивного вызова этого метода, был выбран предыдущий способ вычисления. | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
Вычислительное ядро составляют вычисления элементов матрицы <math>h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}</math>. | Вычислительное ядро составляют вычисления элементов матрицы <math>h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}</math>. | ||
| − | |||
| − | |||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| Строка 89: | Строка 97: | ||
Основную часть метода составляют вычисления значений степени -1 для каждого элемента: | Основную часть метода составляют вычисления значений степени -1 для каждого элемента: | ||
| − | : <math>\sum_{j=0}^ | + | : <math>\sum_{j=0}^n k_j l_j</math>. |
Как видно по формуле, получаемое значение равна количеству единиц в двоичной записи результата побитового умножения ''k'' и ''l''. Существует эффективный метод вычисления количества единиц , сложность которого равна ''m'' операций вычитания и ''m'' операций побитового умножения, где ''m''-искомое количество единиц. | Как видно по формуле, получаемое значение равна количеству единиц в двоичной записи результата побитового умножения ''k'' и ''l''. Существует эффективный метод вычисления количества единиц , сложность которого равна ''m'' операций вычитания и ''m'' операций побитового умножения, где ''m''-искомое количество единиц. | ||
| Строка 97: | Строка 105: | ||
Последовательность исполнения метода следующая: | Последовательность исполнения метода следующая: | ||
| − | 1. Побитовое умножение <math>k\&l</math> | + | 1. Побитовое умножение <math>k\&l</math>; |
| − | |||
| − | |||
| − | + | 2. Вычисление количества единиц двоичной записи; | |
| − | + | 3. Определение знака элемента по степени. | |
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| − | Для построения матрицы Адамара порядка <math>2^n</math> в | + | Для построения матрицы Адамара порядка <math>N=2^n</math> в первом шаге потребуется <math>N^2</math> побитовых умножений ''k&l''. |
| − | + | Во втором шаге, как говорилось выше, сложность метода вычисления количества единиц числа в двоичном представлении равна удвоенному количеству единиц. В наихудшем случае сложность равна <math>2log_2N</math>, при ''k=l=N-1'', а в наилучшем 0. Для нахождения степени всех элементов матрицы потребуются <math> 2N^2\left[\frac{log_2N}{4}\right]</math> операций. В третьем шаге для определения знака потребуется <math>N^2</math> операций, то есть сложность алгоритма | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | :<math> | |
| − | + | T(n) = 2\,(1+\left[\frac{n}{4}\right])\,2^{2n}. | |
| − | + | </math> | |
| − | |||
| − | |||
=== Информационный граф === | === Информационный граф === | ||
| − | + | На рисунке ниже изображен информационный граф алгоритма. | |
| − | + | *<math>k\&l</math> - операция побитового умножения, где <math>k</math> и <math>l</math> соответствующие координаты элемента <math>h_{kl}</math>; | |
| + | * OP - вычисление количества единиц числа в двоичной системе. Состоит из последовательного применения операций вычитания и побитового умножения; | ||
| + | * SGN - определение знака соответствующего элемента. Если результат предыдущего шага четное, то знак положительный, иначе отрицательный. | ||
| − | + | [[file:Hadamar.png|thumb|center|1400px|Рисунок 1. Граф алгоритма.]] | |
| − | + | [[file:OP3.png|thumb|center|1400px|Рисунок 2. Граф OP.]] | |
| − | + | === Ресурс параллелизма алгоритма === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Для построения матрицы порядка <math>N=2^n</math> требуется последовательно выполнить следующие шаги: | |
| − | + | * <math>N^2</math> вычислений побитового умножения, | |
| − | * <math> | + | * для каждого элемента от <math>2</math> до <math>2n</math> операций вычитания и побитового умножения, в зависимости от результата предыдущего шага, |
| − | * <math> | + | * <math>N^2</math> для определения знака значения элемента. |
| + | |||
| + | Таким образом для построения необходимы лишь простые операции вычитания и побитового умножения выполняемые с целыми положительными числами. Стоит заметить что вычисления для каждого элемента не зависят друг от друга. Также можно воспользоваться либо симметричностью матрицы Адамара либо закономерностью областей показанная в пункте 1.1. | ||
| + | Таким образом, основной вклад в высотe ЯПФ вносит операция вычисления количества единиц. Ширина ЯПФ будет равна O(n^2). | ||
| − | + | === Входные и выходные данные алгоритма === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Входные данные''': n - размерность матрицы <math>H_n</math>. | |
| − | ''' | + | '''Объём входных данных''': 1 (число n). |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Выходные данные''': матрица Адамара <math>H_n</math> размерностью <math>2^n\times 2^n</math>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Объём выходных данных''': <math>2^{2n}</math>. | |
| − | + | === Свойства алгоритма === | |
| − | + | * Соотношение последовательной и параллельной сложности: | |
| − | [ | + | Одним из трудных мест параллельной реализации является правильный выбор количества процессов. Рассматривается некоторое фиксированное число процессов <math>P\in \mathbb{N}</math>. Считается, что каждый процесс ''P'' обрабатывает не более чем <math>\left[\frac{2^{2n}}{P}\right]\geq 1</math> элементов. Тогда качественная формула может быть записана таким образом: |
| − | = | + | :<math>T(n,P)=2\,(1+\left[ \frac{n}{4} \right])\,\frac{2^{2n}}{P}</math>. |
| − | + | Неравенство <math>\left[\frac{2^{2n}}{P}\right]\geq 1</math> можно переписать, как <math>log_2\,\sqrt{P}\leq n</math>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Легко увидеть, что минимум функции ''T(n,P)'' будет при максимально возможном ''P'' : <math>log_2\,\sqrt{P}\leq n</math>. Такое ''P'' будет оптимальным числом процессов для алгоритма. В частности, для <math>P=2^p,\,p\in\mathbb{N}</math> оптимальное <math>P = 2^{2n}</math>. | |
| + | :<math>\frac{T(n)}{T(n,p)}=P</math>. | ||
| + | то есть, отношение последовательной и параллельной сложности будет ''линейно'' зависеть от <math>P</math>; | ||
| − | + | * ''Вычислительная мощность'' алгоритма построения матрицы Адамара, как отношение числа операций к суммарному объему входных и выходных данных: | |
| + | :<math>\,\frac{2^{2n}(2+[\frac{n}{4}])}{1+2^{2n}}\left( \sim [\frac{n}{4}],\,n\to+\infty \right).</math>; | ||
| − | + | * Алгоритм построения матрицы Адамара является ''не детерминированным'', так как число операций меняется в зависимости от входных данных (числа n, которое формирует матрицу размерности 2<sup>''n''</sup> × 2<sup>''n''</sup>); | |
| − | + | * Степень исхода вершины информационного графа равна 1; | |
| − | |||
| − | * | ||
| − | |||
| − | ''' | + | * Алгоритм построения матрицы Адамара является ''сбалансированным''. Так как количество вершин на разных процессорах одинаково, то алгоритм является сбалансированным по числу операций на каждом процессоре. |
| − | + | =ЧАСТЬ Программная реализация алгоритма = | |
| − | + | == Особенности реализации последовательного алгоритма == | |
| − | + | В простейшем варианте генерацию матрицы Адамара для нашего алгоритма можно записать так: | |
| − | + | <source lang="C"> | |
| + | void adamar(int** H, int n) // N = 2^n - размерность матрицы | ||
| + | { | ||
| + | int i,j,N; | ||
| + | float h; | ||
| + | h = pow(1/2,n/2); // h - нормализующий множитель | ||
| + | N = pow(2,n); | ||
| − | + | for(i=0;i<N;++i) | |
| + | { | ||
| + | for(j=0;j<N;++j) | ||
| + | { | ||
| + | ij = i & j; | ||
| + | for (l=0;ij;++l) ij&=ij-1; // l - количество единиц бинарного представления ij | ||
| + | if(l%2==0) H[i][j] = h; | ||
| + | else H[i][j] = -h; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| − | + | Также существует рекурсивная реализация метода генерации матрицы Адамара | |
| − | + | <source lang="C"> | |
| + | void adamar_recursion(int** H, int N, int i, int j, int h) // h - нормализующий множитель | ||
| + | { | ||
| + | if(n==1) H[i][j] = h; | ||
| + | else | ||
| + | { | ||
| + | adamar(H, N/2, i, j, h); | ||
| + | adamar(H, N/2, i, N/2+j, h); | ||
| + | adamar(H, N/2, N/2+i, j, h); | ||
| + | adamar(H, N/2, N/2+i, N/2+j, -h); | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| − | + | Или эквивалентный безрекурсивный вариант: | |
| − | [[ | + | <source lang="C"> |
| − | + | void adamar_not_recursion(int** H, int n) // N = 2^n - размерность матрицы | |
| − | + | { | |
| − | + | int i,j,N; | |
| − | + | float h; | |
| − | + | h = pow(1/2,n/2); | |
| − | + | N = pow(2,n); | |
| − | = | + | k=2; |
| + | H[0][0] = h; | ||
| + | |||
| + | while(k<=N) | ||
| + | { | ||
| + | for (i=0; i<k; ++i) | ||
| + | { | ||
| + | for (j=0; j<k; ++j) | ||
| + | { | ||
| + | if (i<k/2 && j<k/2) | ||
| + | { | ||
| + | } | ||
| + | else | ||
| + | { | ||
| + | if(i>=k/2 && j>=k/2) | ||
| + | { | ||
| + | H[i][j] = -(H[i-k/2][j-k/2]); | ||
| + | } | ||
| + | else | ||
| + | { | ||
| + | if (i>j) | ||
| + | { | ||
| + | H[i][j] = H[i-k/2][j]; | ||
| + | } | ||
| + | else | ||
| + | { | ||
| + | H[i][j] = H[i][j-k/2]; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | |||
| + | k=k*2; | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| − | + | Для данного случая, рекурсия является менее эффективной для генерации матрицы Адамара ([https://habrahabr.ru/post/256351/ Хабрахабр. О бедной рекурсии замолвите слово, или всё, что вы не знали и не хотите о ней знать.]). С точки зрения последовательной реализации, генерация матрицы Адамара с помощью adamar_not_recursion будет выигрывать у adamar, так как adamar_not_recursion будет выполнять меньшее количество операций. С точки зрения параллельной реализации adamar имеет 100% парализацию и при определенных условиях будет выигрывать по времени у последовательной (пусть в adamar и будет выполняться большее количество операций, но они являются [https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D1%82%D0%BE%D0%B2%D1%8B%D0%B5_%D0%BE%D0%BF%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D0%B8 битовыми операциями]). | |
== Локальность данных и вычислений == | == Локальность данных и вычислений == | ||
| Строка 222: | Строка 270: | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| + | Задача данного раздела - показать пределы [[глоссарий#Масштабируемость|''масштабируемости'']] алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование [[глоссарий#Сильная масштабируемость|''сильной'']] и [[глоссарий#Слабая масштабируемость|''слабой'']] масштабируемости алгоритма и его реализаций. | ||
| + | |||
| + | Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов). | ||
| + | |||
| + | Ключевой момент данного раздела заключается в том, чтобы показать ''реальные параметры масштабируемости программы'' для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи [4]. При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти. | ||
| + | |||
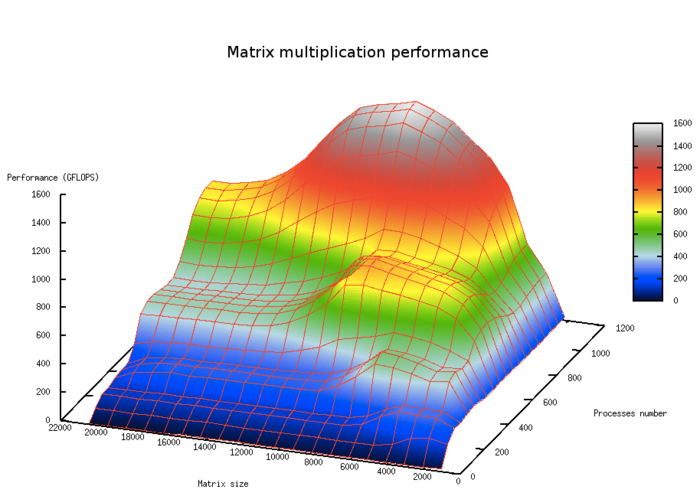
| + | На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти. | ||
| + | [[file:Масштабируемость перемножения матриц производительность.png|thumb|center|700px|Рис.5 Масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи]] | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
| Строка 229: | Строка 285: | ||
== Существующие реализации алгоритма == | == Существующие реализации алгоритма == | ||
| + | Примеры вычислительных пакетов, содержащих функции генерации матриц Адамара: | ||
| + | |||
| + | # [http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter5/hadamard.asp MATLAB]; | ||
| + | # [https://reference.wolfram.com/language/ref/HadamardMatrix.html WOLFRAM]; | ||
| + | # [http://pydoc.net/Python/rogues/0.3.0/rogues.matrices.hadamard/ Python]; | ||
| + | # [http://www.obihiro.ac.jp/~suzukim/masuda/octave/html3/octave_97.html Octave]; | ||
| + | # ... | ||
| + | |||
| + | Стоит отметить, что во многих вычислительных пакетах встроена операция тензорного произведения матриц, которая позволяет строить матрицу Адамара по определению. Этот факт позволяет использовать матрицу Адамара в этих вычислительных пакетах: | ||
| + | # [https://ru.wikipedia.org/wiki/Maple MAPLE]; | ||
| + | # [https://ru.wikipedia.org/wiki/Mathcad MATCATH]; | ||
| + | # ... | ||
= Литература = | = Литература = | ||
| + | [1] Мак-Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с. | ||
| + | |||
| + | [2] Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — Алгебраический аппарат квантовой информатики 2 | ||
| + | |||
| + | [3] Kunz H.O.. On the Equivalence Between One-Dimensional Discrete Walsh-Hadamard and Multidimensional Discrete Fourier Transforms. IEEE Transactions on Computers. 28 (3): 267–8. [https://en.wikipedia.org/wiki/Digital_object_identifier doi]:[http://ieeexplore.ieee.org/document/1675334/ 10.1109/TC.1979.1675334] | ||
| + | [4] Википедия – свободная энциклопедия [Электронный ресурс]. - https://en.wikipedia.org/wiki/Hadamard_transform. - (дата обращения: 15.10.2016). | ||
| + | [5] Воеводин В.В.. Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с. | ||
| − | [ | + | [6] Воронцов К.В.. Математические методы обучения по прецедентам (теория обучения машин) |
Текущая версия на 16:42, 28 октября 2016
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Важную роль в алгебре и комбинаторике играют матрицы Адамара, которые впервые были введены в математический обиход в конце прошлого века одним из крупнейших французских математиков Жаком Адамаром (1865-1963). Их применение в науке и технике посвящены тысячи публикаций. Они предоставляют эффективные возможности для организации хранения, обработки и передачи информации.
Квадратная матрица Н порядка m с элементами ±1 называется матрицей Адамара, если выполняется условие
- [math] H_m\,H_m^T = m\,E_m [/math]
Нетрудно заметить, что различные строки матрицы Адамара попарно ортогональны [1]. Также, можно увидеть из определения, что m четно и
- [math] H_{2m} = \begin{pmatrix} H_{m} & H_{m}\\ H_{m} & -H_{m}\end{pmatrix} [/math]
С матрицами Адамара связан ряд нерешенных проблем, одна из которых состоит в следующем. Мы уже видели, что порядок m матрицы Адамара при m ≥ 3 может быть лишь четным. Более того, при m ≥ 4 порядок обязан делиться на 4. До сих пор остается открытым вопрос: для любого ли m, кратного 4, существует матрица Адамара порядка m? Неизвестно, в частности, существует ли матрица Адамара порядка 268 (это наименьший порядок, кратный 4, для которого матрица Адамара еще не построена).
Часто матрицу Адамара нормализуют и рассматривают размерности степени 2 (например [2],[3] и [4]). В дальнейшем будем рассматривать только такие случаи. Переопределим матрицу Адамара следующим образом:
Матрица Адамара Hn - это матрица размера 2n × 2n, для которой справедливо равенство
- [math]H_n = H_{1} \otimes H_{n-1}[/math],
- [math]\begin{align} H_1 = \frac{1}{\sqrt2} &\begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \end{align}[/math],
где [math] \otimes [/math] представляет собой тензорное произведение.
Представим некоторые частные примеры матриц Адамара:
- [math] H_0 = +1, [/math]
- [math] H_1 = \frac{1}{\sqrt2} \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} [/math],
- [math] H_2 = \frac{1}{2} \begin{pmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{array}\end{pmatrix} [/math],
- [math] H_3 = \frac{1}{2^{\frac{3}{2}}} \begin{pmatrix}\begin{array}{rrrrrrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1\\ 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1\\ 1 & -1 & 1 & 1 & -1 & 1 & -1 & 1\\ 1 & 1 & -1 & 1 & -1 & -1 & 1 & 1\\ 1 & -1 & -1 & -1 & -1 & 1 & 1 & -1\\ \end{array}\end{pmatrix} [/math].
1.2 Математическое описание алгоритма
Основой алгоритма является тот факт, что любую матрицу Адамара [math]H_n[/math], размерностью [math]2^n\times 2^n[/math] можно вычислить поэлементно ([3], [4]):
- [math]h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}[/math],
где kj и lj коэффициенты двоичного разложения чисел k и l (1 или 0):
- [math]k = \sum^{n}_{i=0} {k_i 2^i} = k_{n} 2^{n} + k_{n-1} 2^{n-1} + \cdots + k_1 2 + k_0[/math]
и
- [math]l = \sum^{n}_{i=0} {l_i 2^i} = l_{n} 2^{n} + l_{n-1} 2^{n-1} + \cdots + l_1 2 + l_0[/math].
Помимо этой формулы чаще всего используется заполнение по определению. В связи с трудностями распараллеливания и постоянного выделения памяти при каждом шаге рекурсивного вызова этого метода, был выбран предыдущий способ вычисления.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро составляют вычисления элементов матрицы [math]h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}[/math].
1.4 Макроструктура алгоритма
Основную часть метода составляют вычисления значений степени -1 для каждого элемента:
- [math]\sum_{j=0}^n k_j l_j[/math].
Как видно по формуле, получаемое значение равна количеству единиц в двоичной записи результата побитового умножения k и l. Существует эффективный метод вычисления количества единиц , сложность которого равна m операций вычитания и m операций побитового умножения, где m-искомое количество единиц.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. Побитовое умножение [math]k\&l[/math];
2. Вычисление количества единиц двоичной записи;
3. Определение знака элемента по степени.
1.6 Последовательная сложность алгоритма
Для построения матрицы Адамара порядка [math]N=2^n[/math] в первом шаге потребуется [math]N^2[/math] побитовых умножений k&l. Во втором шаге, как говорилось выше, сложность метода вычисления количества единиц числа в двоичном представлении равна удвоенному количеству единиц. В наихудшем случае сложность равна [math]2log_2N[/math], при k=l=N-1, а в наилучшем 0. Для нахождения степени всех элементов матрицы потребуются [math] 2N^2\left[\frac{log_2N}{4}\right][/math] операций. В третьем шаге для определения знака потребуется [math]N^2[/math] операций, то есть сложность алгоритма
- [math] T(n) = 2\,(1+\left[\frac{n}{4}\right])\,2^{2n}. [/math]
1.7 Информационный граф
На рисунке ниже изображен информационный граф алгоритма.
- [math]k\&l[/math] - операция побитового умножения, где [math]k[/math] и [math]l[/math] соответствующие координаты элемента [math]h_{kl}[/math];
- OP - вычисление количества единиц числа в двоичной системе. Состоит из последовательного применения операций вычитания и побитового умножения;
- SGN - определение знака соответствующего элемента. Если результат предыдущего шага четное, то знак положительный, иначе отрицательный.
1.8 Ресурс параллелизма алгоритма
Для построения матрицы порядка [math]N=2^n[/math] требуется последовательно выполнить следующие шаги:
- [math]N^2[/math] вычислений побитового умножения,
- для каждого элемента от [math]2[/math] до [math]2n[/math] операций вычитания и побитового умножения, в зависимости от результата предыдущего шага,
- [math]N^2[/math] для определения знака значения элемента.
Таким образом для построения необходимы лишь простые операции вычитания и побитового умножения выполняемые с целыми положительными числами. Стоит заметить что вычисления для каждого элемента не зависят друг от друга. Также можно воспользоваться либо симметричностью матрицы Адамара либо закономерностью областей показанная в пункте 1.1. Таким образом, основной вклад в высотe ЯПФ вносит операция вычисления количества единиц. Ширина ЯПФ будет равна O(n^2).
1.9 Входные и выходные данные алгоритма
Входные данные: n - размерность матрицы [math]H_n[/math].
Объём входных данных: 1 (число n).
Выходные данные: матрица Адамара [math]H_n[/math] размерностью [math]2^n\times 2^n[/math].
Объём выходных данных: [math]2^{2n}[/math].
1.10 Свойства алгоритма
- Соотношение последовательной и параллельной сложности:
Одним из трудных мест параллельной реализации является правильный выбор количества процессов. Рассматривается некоторое фиксированное число процессов [math]P\in \mathbb{N}[/math]. Считается, что каждый процесс P обрабатывает не более чем [math]\left[\frac{2^{2n}}{P}\right]\geq 1[/math] элементов. Тогда качественная формула может быть записана таким образом:
- [math]T(n,P)=2\,(1+\left[ \frac{n}{4} \right])\,\frac{2^{2n}}{P}[/math].
Неравенство [math]\left[\frac{2^{2n}}{P}\right]\geq 1[/math] можно переписать, как [math]log_2\,\sqrt{P}\leq n[/math].
Легко увидеть, что минимум функции T(n,P) будет при максимально возможном P : [math]log_2\,\sqrt{P}\leq n[/math]. Такое P будет оптимальным числом процессов для алгоритма. В частности, для [math]P=2^p,\,p\in\mathbb{N}[/math] оптимальное [math]P = 2^{2n}[/math].
- [math]\frac{T(n)}{T(n,p)}=P[/math].
то есть, отношение последовательной и параллельной сложности будет линейно зависеть от [math]P[/math];
- Вычислительная мощность алгоритма построения матрицы Адамара, как отношение числа операций к суммарному объему входных и выходных данных:
- [math]\,\frac{2^{2n}(2+[\frac{n}{4}])}{1+2^{2n}}\left( \sim [\frac{n}{4}],\,n\to+\infty \right).[/math];
- Алгоритм построения матрицы Адамара является не детерминированным, так как число операций меняется в зависимости от входных данных (числа n, которое формирует матрицу размерности 2n × 2n);
- Степень исхода вершины информационного графа равна 1;
- Алгоритм построения матрицы Адамара является сбалансированным. Так как количество вершин на разных процессорах одинаково, то алгоритм является сбалансированным по числу операций на каждом процессоре.
2 ЧАСТЬ Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В простейшем варианте генерацию матрицы Адамара для нашего алгоритма можно записать так:
void adamar(int** H, int n) // N = 2^n - размерность матрицы
{
int i,j,N;
float h;
h = pow(1/2,n/2); // h - нормализующий множитель
N = pow(2,n);
for(i=0;i<N;++i)
{
for(j=0;j<N;++j)
{
ij = i & j;
for (l=0;ij;++l) ij&=ij-1; // l - количество единиц бинарного представления ij
if(l%2==0) H[i][j] = h;
else H[i][j] = -h;
}
}
}
Также существует рекурсивная реализация метода генерации матрицы Адамара
void adamar_recursion(int** H, int N, int i, int j, int h) // h - нормализующий множитель
{
if(n==1) H[i][j] = h;
else
{
adamar(H, N/2, i, j, h);
adamar(H, N/2, i, N/2+j, h);
adamar(H, N/2, N/2+i, j, h);
adamar(H, N/2, N/2+i, N/2+j, -h);
}
}
Или эквивалентный безрекурсивный вариант:
void adamar_not_recursion(int** H, int n) // N = 2^n - размерность матрицы
{
int i,j,N;
float h;
h = pow(1/2,n/2);
N = pow(2,n);
k=2;
H[0][0] = h;
while(k<=N)
{
for (i=0; i<k; ++i)
{
for (j=0; j<k; ++j)
{
if (i<k/2 && j<k/2)
{
}
else
{
if(i>=k/2 && j>=k/2)
{
H[i][j] = -(H[i-k/2][j-k/2]);
}
else
{
if (i>j)
{
H[i][j] = H[i-k/2][j];
}
else
{
H[i][j] = H[i][j-k/2];
}
}
}
}
}
k=k*2;
}
}
Для данного случая, рекурсия является менее эффективной для генерации матрицы Адамара (Хабрахабр. О бедной рекурсии замолвите слово, или всё, что вы не знали и не хотите о ней знать.). С точки зрения последовательной реализации, генерация матрицы Адамара с помощью adamar_not_recursion будет выигрывать у adamar, так как adamar_not_recursion будет выполнять меньшее количество операций. С точки зрения параллельной реализации adamar имеет 100% парализацию и при определенных условиях будет выигрывать по времени у последовательной (пусть в adamar и будет выполняться большее количество операций, но они являются битовыми операциями).
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Задача данного раздела - показать пределы масштабируемости алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование сильной и слабой масштабируемости алгоритма и его реализаций.
Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).
Ключевой момент данного раздела заключается в том, чтобы показать реальные параметры масштабируемости программы для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи [4]. При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.
На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Примеры вычислительных пакетов, содержащих функции генерации матриц Адамара:
Стоит отметить, что во многих вычислительных пакетах встроена операция тензорного произведения матриц, которая позволяет строить матрицу Адамара по определению. Этот факт позволяет использовать матрицу Адамара в этих вычислительных пакетах:
3 Литература
[1] Мак-Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с.
[2] Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — Алгебраический аппарат квантовой информатики 2
[3] Kunz H.O.. On the Equivalence Between One-Dimensional Discrete Walsh-Hadamard and Multidimensional Discrete Fourier Transforms. IEEE Transactions on Computers. 28 (3): 267–8. doi:10.1109/TC.1979.1675334
[4] Википедия – свободная энциклопедия [Электронный ресурс]. - https://en.wikipedia.org/wiki/Hadamard_transform. - (дата обращения: 15.10.2016).
[5] Воеводин В.В.. Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.
[6] Воронцов К.В.. Математические методы обучения по прецедентам (теория обучения машин)