Прямая подстановка (вещественный вариант): различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Frolov (обсуждение | вклад) |
Frolov (обсуждение | вклад) |
||
| Строка 74: | Строка 74: | ||
Опишем [[глоссарий#Граф алгоритма|граф алгоритма]] как аналитически, так и в виде рисунка. | Опишем [[глоссарий#Граф алгоритма|граф алгоритма]] как аналитически, так и в виде рисунка. | ||
| + | |||
| + | [[Файл:DirectL.png|450px|thumb|left|описание]] | ||
Граф алгоритма прямой подстановки состоит из двух групп вершин, расположенных в целочисленных узлах двух областей разной размерности. | Граф алгоритма прямой подстановки состоит из двух групп вершин, расположенных в целочисленных узлах двух областей разной размерности. | ||
| − | |||
=== Описание ресурса параллелизма алгоритма === | === Описание ресурса параллелизма алгоритма === | ||
Версия 16:07, 17 сентября 2014
Содержание
- 1 Описание свойств и структуры алгоритма
- 1.1 Словесное описание алгоритма
- 1.2 Математическое описание
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Описание схемы реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Описание входных и выходных данных
- 1.10 Свойства алгоритма
- 2 Программная реализация
- 3 Литература
1 Описание свойств и структуры алгоритма
1.1 Словесное описание алгоритма
Прямая подстановка - решение СЛАУ Lx = y с левой треугольной матрицей L. Матрица L - одна из составляющих матрицы A и получается либо из LU-разложения последней каким-либо из многочисленных способов (например, простое разложение Гаусса, разложение Гаусса с выбором ведущего элемента, компактная схема Гаусса), либо из других разложений. В силу треугольности L решение СЛАУ является одной из модификаций общего метода подстановки и записывается простыми формулами.
В [1] метод решения СЛАУ с левой треугольной матрицей назван методом обратной подстановки. Там же отмечено, что в литературе иногда под обратной подстановкой имеют в виду, как и здесь, только решения СЛАУ с правой треугольной матрицей, а решение левых треугольных систем называют прямой подстановкой. Такой же системы названий будем придерживаться и мы, во избежание одноимённого названия разных алгоритмов. Кроме того, обратная подстановка, представленная в этой энциклопедии алгоритмов, одновременно является частью метода Гаусса для решения СЛАУ, а именно - его обратным ходом, чего нельзя сказать про представленную здесь прямую подстановку.
Общая структура прямой подстановки с неособенной левой треугольной матрицей, тем не менее, практически полностью совпадает со структурой обратной подстановки. Поэтому здесь мы рассмотрим случай, когда матрица L, как полученная из разложения типа Гаусса, имеет единичные диагональные элементы.
1.2 Математическое описание
Исходные данные: левая треугольная матрица L (элементы l_{ij}), вектор правой части b (элементы b_{i}).
Вычисляемые данные: вектор решения y (элементы y_{i}).
Формулы метода:
- \begin{align} y_{1} & = b_{1} \\ y_{i} & = b_{i} - \sum_{j = 1}^{i-1} l_{ij} y_{j}, \quad i \in [2, n]. \end{align}
Существует также блочная версия метода, однако в данном описании разобран только точечный метод.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро прямой подстановки можно составить из множественных (всего их n-1) вычислений скалярных произведений строк матрицы L на уже вычисленную часть вектора y:
- \sum_{j = 1}^{i-1} l_{ij} y_{j}
в режиме накопления или без него, в зависимости от требований задачи, с их последующим вычитанием из компоненты вектора b и деления на диагональный элемент матрицы L. В отечественных реализациях, даже в последовательных, упомянутый способ представления не используется. Дело в том, что даже в этих реализациях метода вычисление сумм типа
- b_{i} - \sum_{j = 1}^{i-1} l_{ij} y_{j}
в которых и встречаются скалярные произведения, ведутся не в порядке «вычислили скалярное произведение, а потом вычли его из элемента», а путём вычитания из элемента покомпонентных произведений, являющихся частями скалярных произведений. Поэтому следует считать вычислительным ядром метода прямой подстановки не вычисления скалярных произведений, а вычисления выражений
- b_{i} - \sum_{j = 1}^{i-1} l_{ij} y_{j}
в режиме накопления или без него, в зависимости от требований задачи.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть метода прямой подстановки составляют множественные (всего n-1) вычисления сумм
- b_{i} - \sum_{j = 1}^{i-1} l_{ij} y_{j}
в режиме накопления или без него.
1.5 Описание схемы реализации последовательного алгоритма
Чтобы понять последовательность исполнения, перепишем формулы метода так:
1. y_{1} = b_{1}
Далее для всех i от 2 до n по возрастанию выполняются
2. y_{i} = b_{i} - \sum_{j = 1}^{i-1} l_{ij} y_{j}
Особо отметим, что вычисления сумм вида b_{i} - \sum_{j = 1}^{i-1} l_{ij} y_{j} производят в режиме накопления вычитанием из b_{i} произведений l_{ij} y_{j} для j от 1 до i-1, c возрастанием j. Другие порядки выполнения суммирования приводят к резкому ухудшению параллельных свойств алгоритма.
1.6 Последовательная сложность алгоритма
Для прямой подстановки порядка n в последовательном (наиболее быстром) варианте требуется:
- по \frac{n^2-n}{2} умножений и сложений (вычитаний).
При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает затраты во времени, требуемом для выполнения прямой подстановки.
При классификации по последовательной сложности, таким образом, метод обратной подстановки относится к алгоритмам с квадратической сложностью.
1.7 Информационный граф
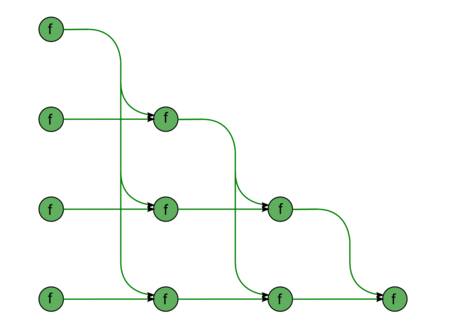
Опишем граф алгоритма как аналитически, так и в виде рисунка.
Граф алгоритма прямой подстановки состоит из двух групп вершин, расположенных в целочисленных узлах двух областей разной размерности.
1.8 Описание ресурса параллелизма алгоритма
Для прямой подстановки порядка n в параллельном варианте требуется последовательно выполнить следующие ярусы:
- по n - 1 ярусов умножений и сложений/вычитаний (в каждом из ярусов — линейное количество операций, от 1 до n-1.
При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти.
При классификации по высоте ЯПФ, таким образом, метод прямой подстановки относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет линейной.
1.9 Описание входных и выходных данных
Входные данные: левая треугольная матрица L (элементы l_{ij}), вектор правой части b (элементы b_{i}).
Объём входных данных: \frac{n (n + 1)}{2} (в силу треугольности и единичности диагональных элементов достаточно хранить только поддиагональные элементы матрицы L).
Выходные данные: вектор решения y (элементы y_{i}).
Объём выходных данных: n.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение квадратической к линейной).
При этом вычислительная мощность алгоритма прямой подстановки, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь константа.
При этом алгоритм прямой подстановки полностью детерминирован. Использование другого порядка выполнения ассоциативных операций в данной версии нами не рассматривается, поскольку в корне меняет структуру алгоритма и делает параллельную сложность квадратической.
2 Программная реализация
2.1 Особенности реализации последовательного алгоритма
В простейшем варианте метод прямой подстановки на Фортране можно записать так:
Y(1) = B(1)
DO I = 2, N-1
S = B(I)
DO J = 1, I-1
S = S - DPROD(L(I,J), Y(J))
END DO
END DO
При этом для реализации режима накопления переменная S должна быть двойной точности.
3 Литература
- В.В.Воеводин, Ю.А.Кузнецов. Матрицы и вычисления. М.: Наука, 1984, стр. 182.