Участник:Emaksimov/Кластеризация сетями Кохонена

Кластеризация сетями Кохонена

Рисунок 1. Кластеризация сетями Кохонена

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Искусственная нейронная сеть Кохонена или самоорганизующаяся карта признаков (SOM) была предложена финским исследователем Тойво Кохоненом в начале 1980-х годов.

Рисунок 2. Кохонен, Теуво.

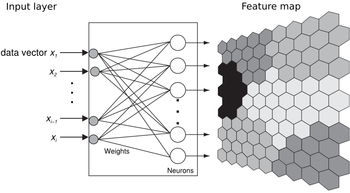
Она представляет собой двухслойную сеть. Каждый нейрон первого (распределительного) слоя соединен со всеми нейронами второго (выходного) слоя, которые расположены в виде двумерной решетки. Нейроны выходного слоя называются кластерными элементами, их количество определят максимальное количество групп, на которые система может разделить входные данные. Увеличивая количество нейронов второго слоя можно увеличивать детализацию результатов процесса кластеризации.

Система работает по принципу соревнования – нейроны второго слоя соревнуются друг с другом за право наилучшим образом сочетаться с входным вектором сигналов, побеждает тот элемент-нейрон, чей вектор весов ближе всего к входному вектору сигналов. За меру близости двух векторов можно взять квадрат евклидова расстояния. Таким образом, каждый входной вектор относится к некоторому кластерному элементу.

Для обучения сети Кохонена используется соревновательный метод. На каждом шаге обучения из исходного набора данных случайно выбирается один вектор. Затем производится поиск нейрона выходного слоя, для которого расстояние между его вектором весов и входным вектором - минимально. По определённому правилу производится корректировка весов для нейрона-победителя и нейронов из его окрестности, которая задаётся соответствующей функцией окрестности.

1.2 Математическое описание алгоритма

Пусть имеется некоторое множество векторов [math] x^{(i)}=(x_1^{(i)},x_2^{(i)},...,x_m^{(i)}) \in \mathbb{R}^m, i=1, \dots, k[/math]. Заранее зададим количество кластеров равным [math]n[/math]. Соответственно, Карта Кохонена представляет собой двухслойную fully-connected нейронную сеть, где первый слой состоит из [math]m[/math] нейронов, а второй - из [math]n[/math]. Каждый j-ый нейрон описывается вектором весов [math] w_j=(w_{1j},w_{2j},...,w_{mj}), j=1, \dots, n[/math].

1.2.1 Алгоритм обучения сети без учителя

Обучение состоит из последовательности коррекций векторов, представляющих собой нейроны.

шаг 0: Подача исходных данных на входы. Весовой вектор [math]w[/math] выбирается случайным образом. Величины [math] \alpha [/math], [math] h_{kc}[/math] известны.

шаг 1: Выбрать произвольное наблюдение [math] x ( t ) [/math] из множества входных данных.

шаг 2: Определить расстояние между между входным вектором и каждого вектора весовых коэффициентов

[math] d_k(t)=||x(t)-w_k(t)||, k=1,...,n[/math],

шаг 3: Определение нейрона -победителя (веса которого в наименьшей степени отличаются от соответствующих компонентов входного вектора)

[math] d_w(t)=\min\limits_{k}(d_k(t)), k=1,...,n[/math]

шаг 4: Векторы весовых коэффициентов обновляются с помощью функции соседства по формуле

[math] w_k(t+1)=w_k(t)+\alpha(t)h_{kc}(t)||x(t)-w_k(t)||,[/math]

шаг 5: Прекратите, если максимальное число итераций достигнуто; в противном случае изменить параметры [math] \alpha [/math] и [math] h_{kc} [/math] продолжите с шага 1 .

Переменные

• [math]t [/math] -текущая итерация
• [math]\lambda [/math] -предельное значение итераций
• [math]x(t)[/math] -вектор входных данных
• [math]k[/math] -индекс узла в карте
• [math]w_k[/math] -текущий вектор веса в узле k
• [math]c[/math] -индекс нейрона-побдителя
• [math] h_{kc}(t)[/math]- функция "соседства", определяет расстояне между нейроном [math] w_k [/math] и [math] w_c [/math]
• [math]\alpha (t)[/math]- монотонно убывающий коэффициент обучения .

Инициализация начальных весов

Удачно выбранный способ инициализации может существенно ускорить обучение, и привести к получению более качественных результатов. Существуют три способа инициирования начальных весов.

• Инициализация случайными значениями, когда всем весам даются малые случайные величины.

• Инициализация примерами, когда в качестве начальных значений задаются значения случайно выбранных примеров из обучающей выборки.

• Линейная инициализация. В этом случае веса инициируются значениями векторов, линейно упорядоченных вдоль линейного подпространства, проходящего между двумя главных собственными векторами исходного набора данных. Собственные вектора могут быть найдены например при помощи процедуры Грама-Шмидта.

Задание [math]h[/math]

Часто в качестве функции соседства используется гауссовская функция:

[math]h_{ci}(t)=\alpha(t)\cdot\exp(-\frac{\|r_c-r_k\|^2}{2\sigma^2(t)})[/math]

где [math]0\lt \alpha(t)\lt 1[/math] — обучающий сомножитель, монотонно убывающий с каждой последующей итерацией (то есть определяющий приближение значения векторов веса нейрона-победителя и его соседей к наблюдению; чем больше шаг, тем меньше уточнение);
[math]r_k[/math], [math]r_c[/math] — координаты узлов [math]W_k(t)[/math] и [math]W_c(t)[/math] на карте;

[math]\sigma(t)[/math] — сомножитель, уменьшающий количество соседей с итерациями, монотонно убывает. Параметры [math]\alpha[/math], [math]\sigma[/math] и их характер убывания задаются аналитиком.

Более простой способ задания функции соседства:

[math]h_{ci}(t)=\alpha(t)[/math], 

если [math]W_k(t)[/math] находится в окрестности [math]W_c(t)[/math] заранее заданного аналитиком радиуса, и 0 в противном случае. Функция [math]h(t)[/math] равна [math]\alpha(t)[/math] для BMU и уменьшается с удалением от BMU.

1.9 Входные и выходные данные алгоритма

При использовании обученной сети

Входные данные: множество входных векторов (нейронов первого уровня), множество кластеров (выходов, нейронов второго уровня)

Выходные данные: кластеризованная выборка - каждому нейрону первого уровня сопоставлен один или несколько нейронов второго уровня (вектор отнесен к одному из кластеров)