Участник:Emaksimov/Кластеризация сетями Кохонена

Кластеризация сетями Кохонена

Рисунок 1. Кластеризация сетями Кохонена

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

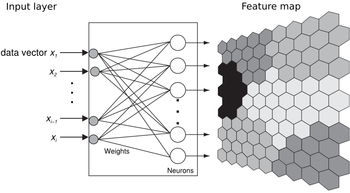
Искусственная нейронная сеть Кохонена или самоорганизующаяся карта признаков (SOM) была предложена финским исследователем Тойво Кохоненом в начале 1980-х годов.

Рисунок 2. Кохонен, Теуво.

Она представляет собой двухслойную сеть. Каждый нейрон первого (распределительного) слоя соединен со всеми нейронами второго (выходного) слоя, которые расположены в виде двумерной решетки. Нейроны выходного слоя называются кластерными элементами, их количество определят максимальное количество групп, на которые система может разделить входные данные. Увеличивая количество нейронов второго слоя можно увеличивать детализацию результатов процесса кластеризации.

Система работает по принципу соревнования – нейроны второго слоя соревнуются друг с другом за право наилучшим образом сочетаться с входным вектором сигналов, побеждает тот элемент-нейрон, чей вектор весов ближе всего к входному вектору сигналов. За меру близости двух векторов можно взять квадрат евклидова расстояния. Таким образом, каждый входной вектор относится к некоторому кластерному элементу.

Для обучения сети Кохонена используется соревновательный метод. На каждом шаге обучения из исходного набора данных случайно выбирается один вектор. Затем производится поиск нейрона выходного слоя, для которого расстояние между его вектором весов и входным вектором - минимально. По определённому правилу производится корректировка весов для нейрона-победителя и нейронов из его окрестности, которая задаётся соответствующей функцией окрестности.

1.2 Математическое описание алгоритма

Пусть имеется некоторое множество векторов $x^{(i)}=(x_1^{(i)},x_2^{(i)},...,x_m^{(i)}) \in \mathbb{R}^m, i=1, \dots, k$. Заранее зададим количество кластеров равным $n$. Соответственно, Карта Кохонена представляет собой двухслойную fully-connected нейронную сеть, где первый слой состоит из $m$ нейронов, а второй - из $n$. Каждый j-ый нейрон описывается вектором весов $w_j=(w_{1j},w_{2j},...,w_{mj}), j=1, \dots, n$.

Алгоритм обучения сети без учителя

Обучение состоит из последовательности коррекций векторов, представляющих собой нейроны. Сначала следует инициализировать векторы весов. Далее определенное количество раз (эпох) производятся следующие действия:

1. Случайным образов выбирается вектор $x(t)$ из входных данных.

1. Выбирается нейрон-победитель $w_c$ "наиболее похожий" (по евклидову расстоянию) на вектор $x(t)$:

$||x(t)-w_c||=\min\limits_{i}(||x(t)-w_i(t)||)$

.

1. Веса всех нейронов обновляются по формуле: $w_i(t+1)=w_i(t)+\alpha(t)h_{ic}(t)||x(t)-w_i(t)||$, где

$t$ - номер эпохи, $h_{ic}(t)$- функция соседства нейронов, $\alpha (t)$ - функция скорости обучения сети.

Инициализация начальных весов

Существуют два способа инициализации весовых коэффициентов: Инициализация случайными значениями, когда всем весам даются малые случайные величины. Инициализация примерами, когда в качестве начальных значений задаются значения случайно выбранных примеров из обучающей выборки.

Функция соседства нейронов

\begin{equation*} X(\omega) =

\begin{cases}
  1 &\text{se $\omega\in A$}\\
  1250 &\text{se $\omega \in A^c$}
\end{cases}

\end{equation*}

Часто в качестве функции соседства используется гауссовская функция:

[math]h_{ci}(t)=\alpha(t)\cdot\exp(-\frac{\|r_c-r_k\|^2}{2\sigma^2(t)})[/math]

где $0\lt \alpha(t)\lt 1$ — обучающий сомножитель, монотонно убывающий с каждой последующей итерацией (то есть определяющий приближение значения векторов веса нейрона-победителя и его соседей к наблюдению; чем больше шаг, тем меньше уточнение);
$r_k$, $r_c$ — координаты узлов $W_k(t)$ и $W_c(t)$ на карте;

$\sigma(t)$ — сомножитель, уменьшающий количество соседей с итерациями, монотонно убывает. Параметры $\alpha$, $\sigma$ и их характер убывания задаются аналитиком.

Более простой способ задания функции соседства:

[math]h_{ci}(t)=\alpha(t)[/math], 

если $W_k(t)$ находится в окрестности $W_c(t)$ заранее заданного аналитиком радиуса, и 0 в противном случае. Функция $h(t)$ равна $\alpha(t)$ для BMU и уменьшается с удалением от BMU.

1.3 Вычислительное ядро алгоритма

На каждом шаге обучения из входного множества случайно выбирается один из векторов, а затем производится поиск наиболее похожего на него вектора коэффициентов нейронов. Выбирается нейрон, наиболее похожий на входной вектор.

1.4 Макроструктура алгоритма

$\mathbf{W} \leftarrow ComputeInitialWeights(\mathbf{W})$

Далее следует цикл, повторяющийся $T_{max}$ (максимальное число "эпох") раз:

1. $\mathbf{W_i} \leftarrow CalculateEucledeNorm(\mathbf{W_i})$
2. $\mathbf{W_i(t+1)}\leftarrow CorrectWeights(\mathbf{W_i(t)})$

1.5 Схема реализации последовательного алгоритма

$\begin{align} \mathbf{W} := InitializeWeights() \\ \mathbf{FOR} \ t := 1 \ \mathbf{TO} \ T_{max} \ \mathbf{DO} \\ \mathcal{B} \leftarrow ChooseRandomVector\left( \{1, \dots, N\} \right) \\ \mathbf{FOR} \ i := 1 \ \mathbf{TO} \ n \ \mathbf{DO} \\ CalculateEucledeNorm(\mathbf{W_i}) \\ \mathbf{W_i(t+1)} \leftarrow CorrectWeights(\mathbf{W_i(t)}) \\ \end{align}$

1.9 Входные и выходные данные алгоритма

Входные данные: множество входных векторов (нейронов первого уровня), множество кластеров (выходов, нейронов второго уровня), максимальное число "эпох" $T_{max}$, константа $\delta$, константы $A$ и $B$, константа $c$ (в случае, если выбрана простая константа).

Выходные данные: матрица весов