Участник:Tereshinvs/MST Clusterization: различия между версиями
| Строка 71: | Строка 71: | ||
Итак, общая сложность алгоритма в общем случае <math>O(N^2 \log N)</math>. | Итак, общая сложность алгоритма в общем случае <math>O(N^2 \log N)</math>. | ||
| + | |||
=== Информационный граф === | === Информационный граф === | ||
| + | [[File:Tereshinvs_mst_scheme.png|center|Информационный граф алгоритма кластеризации на основе минимального остовного дерева]] | ||
| + | |||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
Основным местом для распараллеливания алгоритма является поиск наименьшего ребра из одной компоненты связности в другие. Так как компоненты связности в данном случае независимы, то отдельные узлы вычислительной системы могут выполнять поиск наименьших рёбер независимо. | Основным местом для распараллеливания алгоритма является поиск наименьшего ребра из одной компоненты связности в другие. Так как компоненты связности в данном случае независимы, то отдельные узлы вычислительной системы могут выполнять поиск наименьших рёбер независимо. | ||
Версия 17:24, 15 октября 2016
Содержание
- 1 Структура и свойства алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Структура и свойства алгоритма
1.1 Общее описание алгоритма
Кластеризация -- это задача статистического анализа, состоящая в разбиении множества объектов на группы, называемые кластерами, внутри которых объекты обладают похожими свойствами (чаще всего, это означает близость относительно заданной метрики). Изначально группы неизвестны, в зависимости от постановки задачи может быть также известно или неизвестно общее число кластеров.
Спектр применений кластерного анализа очень широк: его используют в археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, маркетинге, социологии и других дисциплинах.
Постановка задачи также может различаться характером входных данных:
- Набор признаков [math] V = \left\{ v_1, v_2, \ldots, v_N \right\} [/math] в некотором метрическом пространстве с метрикой [math] \rho(x, y) [/math]
- Матрица отношений между объектами: симметричная матрица вещественных чисел размером [math] N \times N [/math] с неотрицательными элементами с нулевой диагональю.
В данной статье рассматривается постановка с известным количеством кластеров [math] K [/math].
Алгоритмы кластеризации делятся на два вида: иерархические и неиерархические. Иерархические алгоритмы строят большие кластеры из меньших или разделяют большие на меньшие, а неиерархические заключаются в минимизации некоторой функции. Примерами неиерархических алгоритмов являются алгоритм k-средних, PAM, CLOPE, LargeItem и т.д., а иерархических -- CURE, ROCK, Chameleon, BIRCH и рассматриваемый в данной статье алгоритм MST (Minimum spanning tree -- минимальное остовное дерево).
Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном взвешенном неориентированном графе -- это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.
Общая схема алгоритма:
- Построение минимального остовного дерева одним из известных методов (алгоритмы Крускала, Прима, Борувки и их комбинации; наиболее пригодным для параллельного исполнения считается алгоритм Борувки)
- Удаление [math] K-1 [/math] самых длинных рёбер из минимального остовного дерева.
В данной статье рассматривается версия алгоритма с использованием алгоритма Борувки.
В случае постановки задачи в виде набора признаков в подходящем метрическом пространстве возможна также предварительная подготовка графа, состоящая из построения триангуляции Делонэ. Так как любое минимальное остовное дерево в этом случае принадлежит триангуляции Делоне, в некоторых случаях это позволяет значительно улучшить ассимптотику алгоритма. Данная часть алгоритма не является обязательной, поэтому подробно рассматриваться не будет.
1.2 Математическое описание алгоритма
Пусть [math]V[/math] — множество объектов, [math]Y[/math] — множество номеров (имён, меток) кластеров. Задана функция расстояния между объектами [math]\rho(x,y)[/math]. Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике [math]\rho[/math], а объекты разных кластеров существенно отличались. При этом каждому объекту [math]v_i\in V[/math] приписывается номер кластера [math]y_i[/math].
Алгоритм кластеризации — это функция [math]a\colon V\to Y[/math], которая любому объекту [math]v\in V[/math] ставит в соответствие номер кластера [math]y\in Y[/math]. Множество [math]Y[/math] в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.
В данном случае задачу можно сформулировать так: выбрать пороговое значение веса ребра [math]W[/math], так чтобы объекты, соединённые ребром весом меньше [math]W[/math] лежали в одном кластере, а соединённые ребром весом больше [math]W[/math] -- в разных.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является построение минимального остовного дерева для графа отношений с помощью алгоритма Борувки. В некоторых случаях построение минимального остовного дерева имеет ту же сложность, что и предварительное построение триангуляции Делонэ, если оно используется.
1.4 Макроструктура алгоритма
Основной алгоритм можно разделить на следующие части:
- Нахождение для каждой вершины наименьшего ребра, инциндентного ней
- Добавление найденных наименьших вершин в MST
- <<Склейка>> компонент связности MST
- Нахождение веса [math]W_{K-1}[/math] [math](K-1)[/math]-ого наибольшего ребра
- Удаление рёбер весом не меньше чем [math]W_{K-1}[/math].
1.5 Схема реализации последовательного алгоритма
0 Ввод: граф V
1
2 Поместить каждую вершину в отдельное дерево леса T
3 Пока в T больше одной компоненты связности:
4 Для каждой компоненты C из T:
5 S -- пустое множество рёбер
6 Для каждой вершины v в C:
7 Найти кратчайшее ребро с одним концом v, а другим не из C, и поместить его в S
8 Добавить кратчайшее ребро из S в T
9 Объединить компоненты связности
10 T -- MST
11
12 Найти W -- вес (K-1)-ого максимального ребра в T
13 Удалить из T рёбра с весом большим или равным W
14
15 Пронумеровать компоненты связности
16
17 Вывод: номера компонент связности для каждой вершины
1.6 Последовательная сложность алгоритма
- Алгоритм Борувки в общем имеет [math]O(\log N)[/math] шагов, а каждый шаг требует [math]O(V)[/math] операций, где [math]V[/math] -- число рёбер в графе. Итого [math]O(V \log N)[/math] операций. При использовании триангуляции Делонэ [math]V[/math] имеет тот же порядок, что и [math]N[/math], поэтому общая сложность [math]O(N \log N)[/math]. В общем же случае сложность составляет [math]O(N^2 \log N)[/math]
- Удаление [math]K-1[/math] рёбер можно осуществить за [math]O(N)[/math] операций.
Итак, общая сложность алгоритма в общем случае [math]O(N^2 \log N)[/math].
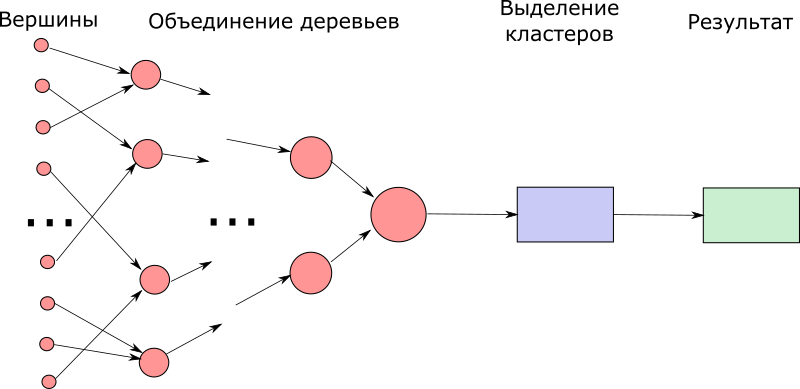
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
Основным местом для распараллеливания алгоритма является поиск наименьшего ребра из одной компоненты связности в другие. Так как компоненты связности в данном случае независимы, то отдельные узлы вычислительной системы могут выполнять поиск наименьших рёбер независимо.
Узким местом является нахождение k-ой порядковой статистики для выделения кластеров, а так же объединение компонент связности. Но всего объединений компонент связности [math]N-1[/math], поэтому при его реализации с помощью структуры данных система непересекабщихся множеств с ранговой эвристикой общая сложность за всё время работы алгоритма будет близко к [math]O(N)[/math].
1.9 Входные и выходные данные алгоритма
Входными данными являются число [math] N [/math] (количество элементов рассматриваемого множества) и матрица вещественных чисел размера [math] N \times N [/math] отношений между элементами этого множества. Матрица предполагается симметричной, а её диагональные элементы равными нулю, поэтому её размер можно оценить как [math] \tfrac{N(N-1)}{2} [/math].
Кроме того, имеется натуральное число [math] K \leqslant N [/math] -- требуемое количество кластеров.
Выходными данными являются [math] N [/math] натуральных чисел от [math] 1 [/math] до [math] K [/math] -- номера кластеров, в которые определена каждая вершина. При этом, каждый кластер содержит хотя бы одну вершину.
1.10 Свойства алгоритма
Чувствителен к выбросам
2 Программная реализация алгоритма
2.1 Масштабируемость алгоритма и его реализации
2.2 Существующие реализации алгоритма
3 Литература
- Euclidean minimum spanning tree, https://en.wikipedia.org/wiki/Euclidean_minimum_spanning_tree
- Нейский И.М. Классификация и сравнение методов кластеризации, http://it-claim.ru/Persons/Neyskiy/Article2_Neiskiy.pdf