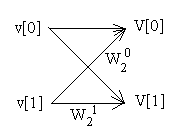Участник:Ivanov.kir.m/Быстрое дискретное преобразование Фурье

Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Kronberg и IgorS.

Алгоритм одномерного преобразования Фурье для действительных чисел
Последовательный алгоритм
Последовательная сложность	$O (N \log N)$
Объём входных данных	$N$ действительных чисел
Объём выходных данных	$\lfloor N/2 \rfloor+1$ комплексных чисел
Параллельный алгоритм
Высота ярусно-параллельной формы	$O (\log N)$
Ширина ярусно-параллельной формы	$N$

Авторы описания К.М.Иванов, А.C.Сапин Вклад каждого участника равномерный, поскольку каждый пункт вычитывался и исправлялся обоими участниками. При сильном приближении можно сказать,что больший вклад К.М.Иванов внес в заполнение теоретической части, а А.C.Сапин в заполнение практической части.

Быстрое преобразование Фурье (БПФ, FFT) — алгоритм быстрого  вычисления дискретного преобразования Фурье (ДПФ). То есть, алгоритм вычисления за количество действий, меньшее чем $O(N^{2})$, требуемых для прямого (по формуле) вычисления ДПФ. Иногда под БПФ понимается один из быстрых алгоритмов, называемый алгоритмом прореживания по частоте/времени или алгоритмом по основанию 2, имеющий сложность $O(N\log(N))$. Cуществует несколько различных алгоритмов для вычисления ДПФ считающимся быстрым преобразование Фурье:

• Алгоритм Кули-Тьюки [1]
• Алгоритм Гуда-Томаса [2]
• Алгоритм Бруна [3]
• Алгоритм Блюштейна [4]

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Быстрое дискретное преобразование Фурье (БПФ) - популярный в современном мире математический метод преобразования вектора/матрицы комплексных/действительных чисел — сигнала — в вектор/матрицу комплексных чисел — спектр. С математической точки зрения преобразование сигнала $s$ (как функции по времени $t$) в спектр $\hat{s}$ описывается формулой

$\hat{s}(\omega)=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{\infty}s(t)e^{-it\omega}\,dt$

В отличие от своего классического аналога, БПФ имеет сложность $O(N\log{N})$, а не $O(N^2)$, это достигается благодаря разделению исходного вектора на несколько частей так, чтобы, применив к этим частям БПФ и объединив результаты путем умножения на поворотные множители и дополнительного БПФ, можно было получить преобразование Фурье исходного вектора — принцип «разделяй и властвуй».

Область применения данного метода простирается от обработки аудио информации до собственно спектрального анализа. Поскольку в общем случае алгоритм БПФ применим к произвольным векторам чисел, выделяют отдельные подзадачи, для которых можно ввести дополнительную оптимизацию. Одной из таких подзадач является быстрое преобразование Фурье вектора действительных чисел, которому и посвящена данная статья. В качестве тестируемой реализации был выбран алгоритм Кули-Тьюки в библиотеке FFTW, написанной на языке C.

Замечание: Поскольку общие описание алгоритма БПФ весьма сложно, в некоторых пунктах данная статья будет ссылаться на простой случай — алгоритм Кули-Тьюки быстрого преобразование Фурье для векторов с размерностью равной степени двойки. Отличительной особенностью данного алгоритма является то, что он обходится без использования специфических приемов, использующихся именно для степеней четверки, восьмерки и т.п. Однако благодаря тому, что на вход данному алгоритму подается вектор чисто вещественных чисел, выходной вектор удовлетворяет эрмитовой избыточности (Hermitian redundancy) , т.е. $out[i]$ является сопряженным с $out[n-i]$. Это обстоятельство позволяет достичь роста скорости и снижения затрат памяти примерно в 2 раза по сравнению с комплексным аналогом алгоритма.

1.2 Математическое описание алгоритма

Входные данные: вектор действительных чисел $x = (x_1,x_2,...,x_N)$.

Выходные данные: вектор комплексных чисел $X = (X_1,X_2,...,X_N)$.

Дискретное преобразование Фурье задается следующей формулой:

$X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} nk}, k = \overline{0,N-1}$

В простейшем случае(для степеней двойки) алгоритм Кули-Тьюки рассчитывает ДПФ для четных $(x_{2m}=x_0, x_2, \ldots, x_{N-2})$ и нечетных элементов отдельно $(x_{2m+1}=x_1, x_3, \ldots, x_{N-1})$. Затем результаты рассчетов объединяются для получения ДПФ всей последовательности:

$\begin{matrix} X_k & = & \sum \limits_{m=0}^{N/2-1} x_{2m}e^{-\frac{2\pi i}{N} (2m)k} + \sum \limits_{m=0}^{N/2-1} x_{2m+1} e^{-\frac{2\pi i}{N} (2m+1)k} \end{matrix}$

Таким образом, получается рекурсивный алгоритм, работающий по принципу разделяй и влавствуй.

1.2.1 Рекурсивное описание

Алгоритм:

1. Входной вектор $a = (a_0,a_2,...,a_{N-1})$ преобразуется в матрицу $A$ размера $n_1 \times n_2$, где $N=n_1 \cdot n_2$ и $n_1 \lt n_2$

$A = \begin{pmatrix} a_0 & a_1 & \cdots & a_{n_1-1} \\ a_{n_1} & a_{n_1+1} & \cdots & a_{2n_1-1} \\ \vdots & \vdots & \ddots & \vdots \\ a_{(n_2-1)\cdot n_1} & a_{(n_2-1)\cdot n_1+1} & \cdots & a_{n_2\cdot n_1-1} \end{pmatrix}$

1. К каждой строке полученной матрицы применяется быстрое дискретное преобразование Фурье (БПФ) порядка $n_1$
2. Каждый элемент полученный после применения БПФ умножается на поворотные множители $exp (2 \pi i(m-1)(j-1)/N)$, где $m$ - номер строки, а $j$ - номер столбца
3. Полученная после шагов 1-2 матрица $A$ транспонируется
4. К каждой строке матрицы $A^T$ применяется БПФ порядка $n_2$

Так как алгоритм реализует принцип «разделяй и властвуй», глубина рекурсии составляет $O (\log N)$ от числа входных элементов.

Замечание: Как правило все поворотные множители вычисляются заранее и хранятся в специальном массиве.

Замечание: В общем случае $N$ разбивается на $n_1 \cdot n_2$ так, чтобы $n_1$ и $n_2$ сами не являлись простыми числами и разлагались на множители, не являющиеся простыми числами.

Замечание: В случае простого $N$ оно дополняется(как правило единицей) до составного числа. В процессе слияния добавленные значения отбрасываются.

1.3 Вычислительное ядро алгоритма

В случае размерности входа равной степени двойки, вычислительным ядром алгоритма является так называемая, "бабочка". В простейшем случае "бабочка" представляет из себя двухточечное преобразование. Рассмотрим этот случай:

На вход алгоритму подается двухэлементный вектор ‒ $v = (v[0], v[1])$. Тогда для вычисления будут происходить по следующим формулам:

$V[0] = W_2^0 v[0] + W_2^0 v[1] = v[0] + W_2^0 v[1]$

$V[1] = W_2^0 v[0] + W_2^1 v[1] = v[0] + W_2^1 v[1]$

Данный процесс удобно изобразить с помощью следующей схемы:

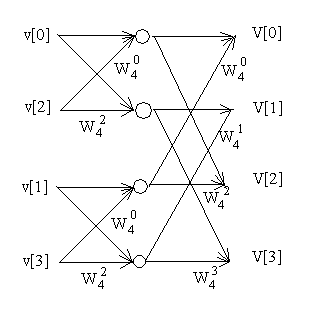
Для 4-х элеметного вектора $v=(v[0],v[1],v[2],v[3])$, алгоритм строится похожим образом. Сначала создаются простейшие "бабочки", а потом их результаты соединяются с противоположеной "бабочкой":

$V[0]=v[0]+W_2^0 v[2]+W_4^0(v[1]+W_2^0 v[3])$

$V[1]=v[0]-W_2^0 v[2]+W_4^1(v[1]-W_2^0 v[3])$

$V[2]=v[0]+W_2^0 v[2]-W_4^0(v[1]+W_2^0 v[3])$

$V[3]=v[0]-W_2^0 v[2]-W_4^1(v[1]-W_2^0 v[3])$

Схема в таком случае будет выглядеть следующим образом:

Для случая, когда вход не является степенью двойки, "бабочки" будут "несимментричными", но в остальном вычисления будут проходить схожим образом.

1.4 Макроструктура алгоритма

Для исходного вектора $a = (a_1,a_2,...,a_N)$ размерности $N = n_1 \cdot n_2$, $n_1 \lt n_2$ БПФ представляется как:

1. $n_2$ БПФ порядка $n_1$
2. $n_1 \cdot n_2$ умножение комплексных чисел
3. $n_1$ БПФ порядка $n_2$

1.5 Схема реализации последовательного алгоритма

Схема организации состоит в том, что на каждом шаге $i$ для выполнения "бабочки" все элементы разбиваются на $n_{i_1}$ векторов по $n_{i_2}$ элементов, причем $n_{i_1} \cdot n_{i_2} = n_i$, где $n_i$ длина входного вектора на текущем шаге $i$. В случае если такое разбиение невозможно, по причине того что $n_i$ простое число, исходный вектор на текущем шаге дополняется элементом. В зависимости от номера шага, разница координат для каждой пары элементов увеличивается соразмерно разбиению $(n_{i_1},n_{i_2})$. При этом результат суммы записывается в элемент с меньшим номером, а результат вычитания с последующим умножением - в элемент с большим.

1.6 Последовательная сложность алгоритма

Быстрое дискретное преобразование Фурье выполнимо за $O(N(n_1+\cdots+n_m))$ действий при $N=n_1n_2\cdots n_m$ (в простом случае, при $N=2^m$ необходимо $O(N\log_2(N))$ действий). Дискретное преобразование Фурье преобразует вектор $a = (a_0, \dots, a_{N-1})$ в вектор комплексных чисел $b = (b_0, \dots, b_{N-1})$, такой, что $b_i=\sum_{j=0}^{N-1}a_j\varepsilon^{ij}$, где $\varepsilon^n=1$ и $\varepsilon^k\neq 1$ при $0\lt k\lt N$.

Основной шаг алгоритма состоит в сведении задачи для $N$ чисел к задаче для $n_1=N/n_2$ числам, где $n_2$ — делитель $N$.

Пусть мы уже умеем решать задачу для $N/n_2$ чисел. Применим преобразование Фурье к векторам $a_i,a_{n_2+i}, \dots, a_{n_2(n_1-1)+i}$ для $i=0,1,\dots,n_2-1$. Покажем теперь, что за $O(Np)$ действий можно решить исходную задачу. Заметим, что $b_i=\sum_{j=0}^{n_2-1} \varepsilon^{ij} \left(\sum_{k=0}^{n_1-1}a_{kn_2+j}\varepsilon^{kin_2}\right)$. Выражения в скобках нам уже известны — это $(i\mod p)$-тое число после преобразования Фурье $j$-го вектора. Таким образом, для вычисления каждого $b_i$ нужно $O(n_2)$ действий, а для вычисления всех $b_i$ всего $O(Nn_2)$ действий, что и требовалось.

В общем случае:

Пусть $4N\gt 2^k\ge2N$. Заметим, что тогда $b_i=\varepsilon^{-i^2/2}\sum_{j=0}^{N-1}\varepsilon^{(i+j)^2/2}\varepsilon^{-j^2/2}a_j$. Обозначим $\bar{a}_i=\varepsilon^{-i^2/2}a_i$, $\bar{b}_i=\varepsilon^{i^2/2}b_i$, $c_i=\varepsilon^{(2N-2-i)^2/2}$. Тогда $\bar{b}_i=\sum_{j=0}^{2N-2-i}\bar{a}_jc_{2N-2-i-j}$, если положить $\bar{a}_i=0$ при $i\ge N$.

Таким образом задача сведена к вычислению свёртки, а это можно сделать с помощью трёх преобразований Фурье для $2^k$ элементов. Выполняем прямое преобразование Фурье для $(\bar{a_0}, \cdots, \bar{a}_{2^k-1})$ и $(c_1,\cdots,c_{2^k-1})$, перемножаем поэлементно результаты и выполняем обратное преобразование Фурье.

Вычисления всех $\bar{a}_i$ и $c_i$ требуют $O(N)$ действий, три преобразования Фурье требуют $O(N\log(N))$ действий, перемножение результатов преобразований Фурье требует $O(N)$ действий, вычисление всех $b_i$ зная значения свертки требует $O(N)$ действий. Итого для дискретного преобразования Фурье требуется $O(N\log(N))$ действий для любого $N$.

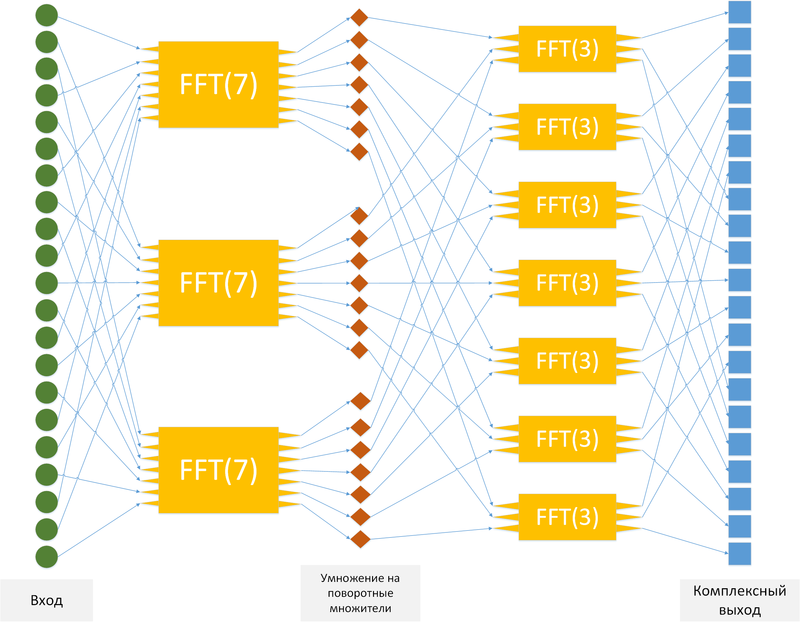
1.7 Информационный граф

Информационный граф алгоритма Кули-Тьюки для $N = 21$. Исходные данные обозначены зеленым, результат — синим. Преобразования Фурье для $n_1 = 7$ и $n_2 = 3 \text{ } (N = n_1 \cdot n_2)$ представлены как «чёрные ящики». Умножение на поворотные коэффициенты (множители) представлено коричневыми ромбами.

Как видно из рисунка, размер этого графа линейно-логарифмический, а формулы дуг имеют экспоненциальные компоненты.

1.8 Ресурс параллелизма алгоритма

Если считать только главные члены выражений, то простой алгоритм Кули-Тьюки имеет критический путь, состоящий из $log(N)$ операций комплексного сложения/вычитания и $log(N)$ операций комплексного умножения (основание $log$ целиком зависит от выбранного на каждом шаге алгоритма разбиения). Здесь стоит отметить, что все рекурсивные вызовы БПФ на каждом шаге выполняются независимо, это приводит к тому, что их можно распределить по доступным вычислительным узлам. Аналогичная ситуация обстоит и с умножением на поворотные множетели, что позволяет независимо присоединять его к любому шагу. Таким образом алгоритм БПФ имеет высокий ресурс параллелизма, а алгоритм БПФ в общем случае может быть отнесён к логарифмическому классу по параллельной сложности.

Кроме того, параллелизм БПФ можно увеличить, если брать $n_1$ и $n_2$ по возможности близкими к кратным доступному количеству вычислительных узлов (а не брать просто один из множителей близким к нулю, как в традиционной реализации), это позволит равномерно распределить работу между вычислительными узлами, что сильно повысит эффективность алгоритма благодаря лишь одной внутренней пересылке данных.

1.9 Входные и выходные данные алгоритма

Входные данные: вектор действительных/комплексных чисел $a = (a_1,a_2,...,a_N)$.

Выходные данные: вектор комплексных чисел $b = (b_1,b_2,...,b_{\lfloor N/2 \rfloor+1})$.

Есть несколько ситуаций, при которых количество потребляемой памяти для хранения входного вектора $a$ и выходного вектора $b$ тможет быть снижено вдвое:

1. Если $a$ — вектор действительных чисел, тогда $b = E\bar{b}$;
2. Если $a$ — вектор чисто-мнимых чисел, тогда $b = -E\bar{b}$;
3. Если $a = E\bar{a}$, тогда $b$ — вектор действительных чисел;
4. Если $a = -E\bar{b}$, то $b$ — вектор чисто-мнимых чисел.

Где матрица $E$:

$E = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & 0 & \cdots & 0 & 1 \\ 0 & 0 & 0 & \cdots & 1 & 0 \\ 0 & 0 & 0 & \ddots & 0 & 0 \\ 0 & 0 & 1 & \cdots & 0 & 0 \\ 0 & 1 & 0 & \cdots & 0 & 0 \end{bmatrix}$

1.10 Свойства алгоритма

Таким образом в общем у алгоритма БПФ в случае неограниченных ресурсов:

• последовательная сложность - линейно-логарифмическая
• параллельная сложность - логарифмическая.

При этом алгоритм полностью детерминирован.

2 ЧАСТЬ. Программная реализация алгоритма

В качестве тестируемой реализации была выбрана библиотека FFTW, а именно функция, выполняющая БПФ одномерного вектора действительных чисел.

2.1 Особенности последовательной реализации алгоритма

Простейший вариант алгоритма для степеней двойки на языке C:

#include <stdio.h>
#include <math.h>
#include <complex.h>

typedef double complex cplx;
 
void _fft(cplx *buf, cplx *out, int n, int step)
{
    if (step < n) {
	_fft(out, buf, n, step * 2); //рекурсивный рассчет
	_fft(out + step, buf + step, n, step * 2);
 
	for (int i = 0; i < n; i += 2 * step) {
	    cplx t = cexp(-I * PI * i / n) * out[i + step];
	    buf[i / 2]     = out[i] + t;
	    buf[(i + n)/2] = out[i] - t;
        }
    }
}
 
void fft(cplx *buf, int n)
{
    cplx out[n];
    for (int i = 0; i < n; i++) out[i] = buf[i];
 
    _fft(buf, out, n, 1);
}

2.4 Масштабируемость алгоритма и его реализации

Тестирование проводилось на вычислительном комплексе IBM Blue Gene/P

2.4.1 Описание платформы IBM Blue Gene/P

IBM Blue Gene/P — массивно-параллельная вычислительная система, которая состоит из двух стоек, включающих 8192 процессорных ядер (2 x 1024 четырехъядерных вычислительных узлов), с пиковой производительностью 27,9 терафлопс (27,8528 триллионов операций с плавающей точкой в секунду).

Характеристики системы:

• две стойки с вычислительными узлами и узлами ввода-вывода
• 1024 четырехъядерных вычислительных узла в каждой из стоек
• 16 узлов ввода-вывода в стойке (в текущей конфигурации активны 8, т.е. одна I/O-карта на 128 вычислительных узлов)
• выделенные коммуникационные сети для межпроцессорных обменов и глобальных операций
• программирование с использованием MPI, OpenMP/pthreads, POSIX I/O
• высокая энергоэффективность: ∼ 372 MFlops/W (см. список Green500)
• система воздушного охлаждения

Стойка (rack, cabinet) состоит из двух midplane'ов. В midplane входит 16 node-карт (compute node card), на каждой из которых установлено 32 вычислительных узла (compute card). Midplane, 8 x 8 x 8 = 512 вычислительных узлов, — минимальный раздел, на котором становится доступна топология трехмерного тора; для разделов меньших размеров используется топология трехмерной решетки. Node-карта может содержать до двух узлов ввода-вывода (I/O card). Вычислительный узел включает в себя четырехъядерный процессор, 2 ГБ общей памяти и сетевые интерфейсы.

Микропроцессорное ядро:

• модель: PowerPC 450
• рабочая частота: 850 MHz
• адресация: 32-битная
• кэш инструкций 1-го уровня (L1 instruction): 32 KB
• кэш данных 1-го уровня (L1 data): 32 KB
• кэш предвыборки (L2 prefetch): 14 потоков предварительной выборки (stream prefetching): 14 x 256 байтов
• два блока 64-битной арифметики с плавающей точкой (Floating Point Unit, FPU), каждый из которых может выдавать за один такт результат совмещенной операции умножения-сложения (Fused Multiply-Add, FMA)
• пиковая производительность: 2 FPU x 2 FMA x 850 MHz = 3,4 GFlop/sec per core

Вычислительные узлы и I/O-карты в аппаратном смысле неразличимы и являются взаимозаменяемыми, разница между ними состоит лишь в способе их использования. У них нет локальной файловой системы, поэтому все операции ввода-вывода перенаправляются внешним устройствам.

Вычислительной узел:

• четыре микропроцессорных ядра PowerPC 450 (4-way SMP)
• пиковая производительность: 4 cores x 3,4 GFlop/sec per core = 13,6 GFlop/sec
• пропускная способность памяти: 13,6 GB/sec
• 2 ГБ общей памяти
• 2 x 4 МБ кэш-памяти 2-го уровня (в документации по BG/P носит название L3)
• легковесное ядро (compute node kernel, CNK), представляющее собой Linux-подобную операционную систему, поддерживающую значительное подмножество Linux-совместимых системных вызовов
• асинхронные операции межпроцессорных обменов (выполняются параллельно с вычислениями)
• операции ввода-вывода перенаправляются I/O-картам через сеть коллективных операций

2.4.2 Оценка масштабируемости алгоритма

Масштабируемость алгоритма проверялась с помощью тестовой программы расположенной по ссылке. Для эксперимента использовались:

• Компилятор mpicc
• Библиотека OpenMPI версии 1.68
• Библиотека FFTW 3.3.5

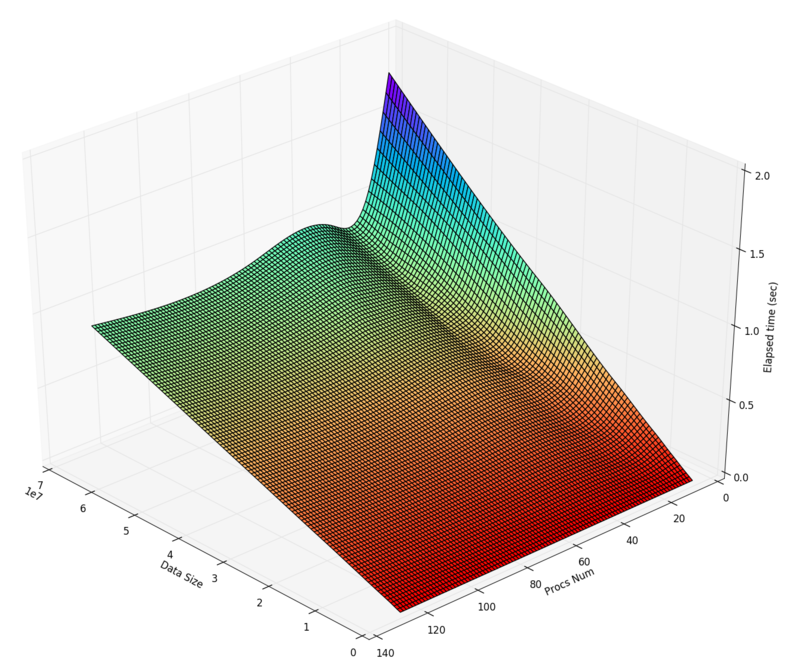
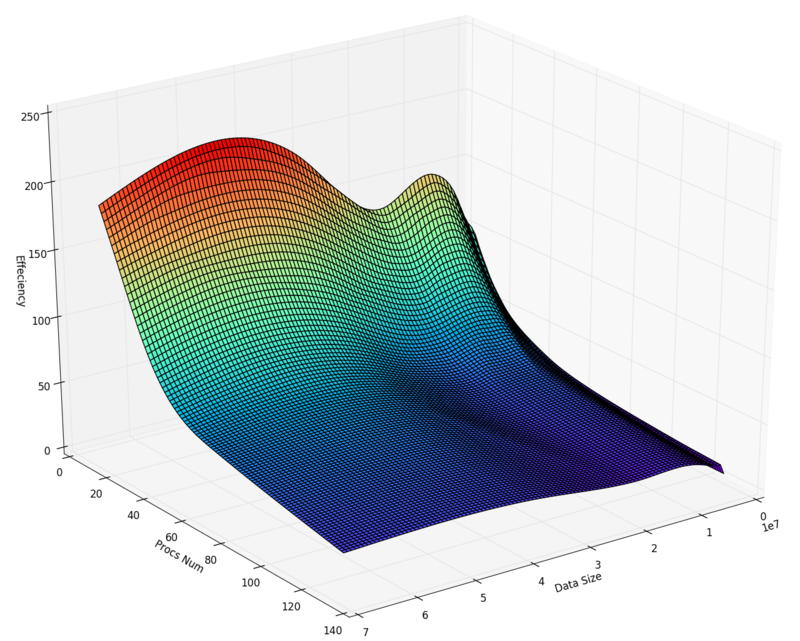
Алгоритм тестировался на входных векторах размера $2^{15}$ до $2^{26}$. При этом использовались от 8 до 128 процессоров с шагом степени двойки.

Замеры времени работы параллельной реализации FFTW для входного вектора действительных чисел. По оси Data Size указано $N$ -- число входных элементов. По оси Procs Num указано $p$ -- число задействованных процессоров. По оси Elapsed Time -- время затраченное на выполненине алгоритма в секундах.

Эффективность параллельной реализации FFTW для входного вектора действительных чисел. По оси Data Size указано $N$ -- число входных элементов. По оси Procs Num указано $p$ -- число задействованных процессоров. По оси Effeciency -- эффективность алгоритма в процентах.

Из графиков можно сделать следующие выводы:

• Значительное увеличение числа процессоров не дает значимого уменьшения времени исполнения, что отражено и на графике эффективности. Это означает, что время, в основном, расходуется на пересылки данных, а не на рассчет.
• При большом количестве элементов и маленьком числе процессоров наблюдается сверхлинейное ускорение, что связано с маленьким число пересылок и активным использованием кеша.

2.7 Существующие реализации алгоритма

Наиболее известной библиотекой для выполнения различных вариантов быстрого преобразования Фурье является FFTW, разработанная Матео Фриго и Стивеном Джонсоном в Массачусетском технологическом институте. Для преобразования небольших объемов данных используется алгоритм Кули - Тьюки, в случае входа больших размеров используется алгоритм Радера или Блюштейна. Библиотека считается самой быстрой реализацией БПФ и на входах любых размеров и размерностей сохраняет ассимптотическую сложность $O(N\cdot log(N))$. Также, существует версия FFTW с поддержкой MPI, которая позволяет с объемами данных не умещающимися в память.

FFTW изначально написана на языке C, однако имеет API для нескольких языков, в том числе Fortran и Ada. Открытая версия библиотеки распространяется под лицензией GNU General Public License. Также существует реализация для коммерческого использования распространяемая под лицензией MIT.

Существует несколько реализаций алгоритма, для рассчета на GPU:

• cuFFT для рассчета на графических ускорителях от NVIDIA.
• clFFT для рассчета на GPU и CPU.

3 Литература

[1] Википедия [Электронный ресурс]. Тема: Быстрое преобразование Фурье – Электрон. дан. – URL Быстрое преобразование Фурье (дата обращения 17.09.2016)

[2] Бахвалов Н. С., Жидков Н. П., Кобельков. Г. М. — 6-е изд. — М. : БИНОМ. Лаборатория знаний, 2008. — 636 с.

[3] FFTW [Электронный ресурс]. Тема: One-Dimensional DFTs of Real Data – Электрон. дан. – URL One-Dimensional DFTs of Real Data (последняя дата обращения 14.19.2016)

[4] FFTW [Электронный ресурс]. – Электрон. дан. – URL FFTW Lib (последняя дата обращения 14.19.2016)