Участник:Grinch96/QR-факторизация методом Грама-Шмидта с последующей реортогонализацией

Автор: Г. А. Балыбердин

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Пусть [math]A = (a_1, ..., a_n)[/math] - вещественная матрица [math]n × n[/math], определитель которой не равен [math]0[/math]. Во многих приложениях требуется решать линейную систему [math]Ax=b[/math] c плохо-обусловленной матрицей [math]A[/math]. При решении данной задачи, чтобы не увеличивать число обусловленности матрицы [math]A[/math], ее можно представить в виде [math]A=QR[/math], где матрица [math]Q \in \mathbb{R}^{n×n}[/math] состоит из ортонормированных строк, а матрица [math] R \in \mathbb{R}^{n×n}[/math] является верхнетреугольной. В итоге мы получаем так называемую [math]QR[/math]-факторизацию.

Чтобы построить [math]QR[/math]-факторизацию можно воспользоваться процессом ортогонализации Грама-Шмидта, однако в условиях машинной арифметики, матрица [math]Q[/math] может получиться далекой от ортогональной.Чтобы этого избежать, на определенных итерациях нужно проводить процесс реортогонализации .

1.2 Математическое описание алгоритма

Исходные данные: квадратная матрица [math]A[/math] порядка [math]n[/math] (элементы [math]a_{ij}[/math]), определитель которой не равен [math]0[/math].

Вычисляемые данные: верхнетреугольная матрица [math]R[/math] порядка [math]n[/math] (элементы [math]r_{ij}[/math]), унитарная матрица [math]Q[/math] порядка [math]n[/math] (элементы [math]q_{ij}[/math]); выполняется соотношение [math]QR=A[/math].

Формулы процесса ортогонализации:

[math] \begin{align} & p_{j} = a_{j} - \sum_{i=1}^{j-1} q_{i} (q_{i}^{T} a_{j}), \\ & q_{j} = p_{j} / ||p_{j}||_{2}, \\ & r_{ij} = q_{i}^{T} a_{j},\quad i = 1, \ldots , j - 1.\\ \end{align} [/math]

Здесь [math]q_{i}, \, a_{i} [/math] столбцы матриц [math] Q, \, A [/math] соответственно.

На [math]m[/math]-ом шаге получаем [math]p_{m} \in \mathbb{R}^{n}[/math]. Если [math]||a_{m}||_{2}/||p_{m}||_{2} \gt k[/math], запускается процесс реортогонализации. [math]k[/math] произвольная и задает точность ортогональности матрицы [math]Q[/math]. В посвященной методу реортогонализации статье [math]k[/math] рекомендуется брать равным [math]10[/math], однако приводятся примеры алгоритмов, где [math]k=\sqrt{2}[/math] или [math]k=\sqrt{5}[/math]. Мы исследуем [math]k=10[/math].

Суть процесса реортогонализации - это процесс ортогонализации Грама-Шмидта, примененный повторно к вектору [math]p_{m}[/math] на [math]m[/math]-оm шаге алгоритма. Более формально:

[math] \begin{align} & \tilde{p}_{m} = p_{m} - \sum_{i=1}^{m-1} q_{i} (q_{i}^{T} p_{m}), \\ & q_{m} = \tilde{p}_{m} / ||\tilde{p}_{m}||_{2}, \\ & \tilde{r}_{mj} = q_{j}^{T} p_{m}, \quad j = 1, \ldots , m - 1, \\ & r_{mj} = \tilde{r}_{mj} + r_{mj}^{0}, \quad j = 1, \ldots , m - 1, \\ & r_{mm} = ||\tilde{p}_{m}||_{2}. \end{align} [/math]

Здесь [math]\tilde{q}_{i}[/math] столбцы матриц [math] \tilde{Q}_{m}[/math], [math]r_{mj}^{0}[/math] - элементы матрицы [math]R[/math], вычисленные до реортогонализации.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма, если не требуется реортогонализация, состоит из вычисления:

• [math]\dfrac{n(n+1)}{2}[/math] скалярных произведений векторов, включая вычисление длины вектора;

• [math]\dfrac{(n-1)n}{2}[/math] умножений векторов на число.

На каждом шаге реортогонализации добавляется [math] j-1 [/math] вычислений скалярных произведений векторов на число и столько же умножений вектора на число. Здесь реортогонализация производится на [math]j[/math]-ом шаге. Однако сколько раз алгоритм будет реортогонализовывать вектора зависит от свойств матрицы.

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть процесса составляют скалярные произведения векторов и умножения вектора на число:

[math] \begin{align} & p_{j} = a_{j} - \sum_{i=1}^{j-1} q_{i} (q_{i}^{T} a_{j}), \\ & q_{j} = p_{j} / ||p_{j}||_{2}. \end{align} [/math]

как если алгоритм реортогонализует повторно вектора, так и без реортогонализаций.

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения процесса следующая:

1. [math] q_1 = \frac{a_1}{||a_1||_2} [/math]

Далее для всех [math] i = 2, n [/math]:

2. [math] r_{ij} = q_{j}^{T} a_{i},\quad j = 1, \ldots , i - 1 [/math]

3. [math] p_{i} = a_{i} - \sum_{j=1}^{i-1} q_{j} r_{ij}[/math]

Если [math]||a_{i}||_{2}/||p_{i}||_{2} \gt k[/math], выполнить 4, 5, 6. Иначе перейти сразу к 7:

4. [math] r_{ij}^{0} = q_{j}^{T} p_{i},\quad j = 1, \ldots , i - 1 [/math]

5. [math] p_{i} = p_{i} - \sum_{j=1}^{i-1} q_{j} r_{ij}^{0}, \quad j = 1, \ldots , i - 1 [/math]

6. [math] r_{ij} = r_{ij}^{0} + r_{ij},\quad j = 1, \ldots , i - 1 [/math]

7. [math] r_{ii} = ||p_{i}||_{2} [/math]

8. [math] q_{i} = p_{i} / r_{ii} [/math]

Здесь (как и везде) под второй нормой подразумевается:

[math] ||x||_2 = \sqrt{x_1^2 + x_2^{2} + \ldots + x_n^2} [/math]

1.6 Последовательная сложность алгоритма

Для факторизации матрицы порядка n процессом Грама-Шмидта в последовательном варианте без реортогонализации требуется:

• [math]n[/math] извлечений квадратного корня,
• [math]n[/math] делений,
• [math](n-1)(n^2+2n-1)[/math] сложений (вычитаний),
• [math]n(n^2+2n-2)[/math] умножений.

Если реортогонализация работает на каждом шаге (чего никогда не случается, однако предположим худший случай), то количество всех операций удвоится. Таким образом, умножения и сложения (вычитания) составляют основную часть алгоритма.

При классификации по последовательной сложности, процесс ортогонализации Грама-Шмидта с реортогонализацией относится к алгоритмам с кубической сложностью.

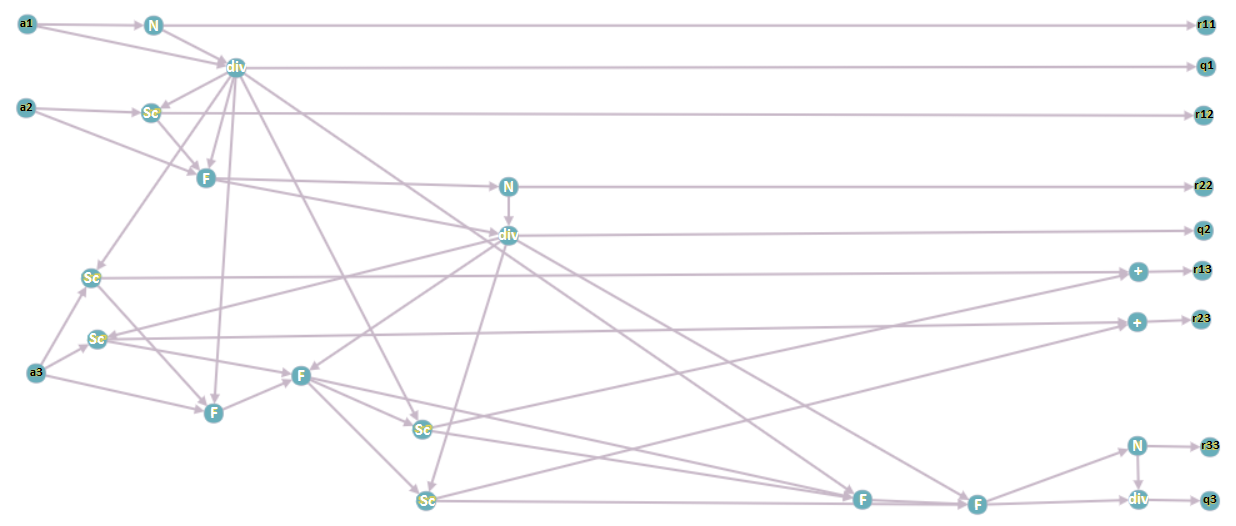
1.7 Информационный граф

Опишем вершины информационного графа.

1. [math] a_i, \; i = 1 \ldots n [/math] — столбцы исходной матрицы [math] A [/math]; подаются на вход программе.

2. [math] N [/math] — операция взятия нормы вектора.

3. [math] div [/math] — операция деления вектора на число.

4. [math] Sc [/math] — операция взятия скалярного произведения двух векторов.

5. [math] F [/math] — операция вычитания из вектора произведение числа на вектор.

6. [math] + [/math] — операция суммирования двух чисел.

7. [math] r_{ij} [/math], [math] q_i, \; i = 1 \ldots n, \; j = 1 \ldots n [/math] — элементы матрицы [math] R [/math] и столбцы матрицы [math] Q [/math] соответственно; выходные данные программы.

Информационный граф построен для матрицы размерности [math] 3 [/math] при выполнении реортогонализации для третьего вектора.

Если объединить вершины N и div, Sc и F (вершины будут означать суперпозиции соответствующих операций), то получится следующий, чуть более простой для понимания, граф:

1.8 Ресурс параллелизма алгоритма

В последовательной версии алгоритма двумя самыми трудоемкими операциями являются подсчет скалярных произведений и вычисление вектора, ортогонального предыдущим. Мы хотим добиться, чтобы каждый процессор считал "кусок" этих операций, однако также для ускорения работы программы нужно минимизировать число пересылок между процессорами. Пусть [math] k [/math] - количество процессоров. Предлагается разбить исходную матрицу [math] A [/math] на [math] k [/math] блоков по [math] \frac{n}{k} [/math] столбцов в каждом ([math] n [/math] - размерность задачи), тогда каждый процессор будет решать задачу на "своем подпространстве". Таким образом мы добьемся количества пересылок порядка [math] O(kn) [/math], и параллельная сложность алгоритма составит [math] O( \frac{n^3}{k} ) [/math].

1.9 Входные и выходные данные алгоритма

Входные данные: невырожденная матрица [math]A[/math] (элементы [math]a_{ij}[/math]).

Объём входных данных: [math]n^2[/math].

Выходные данные: верхняя треугольная матрица [math]R[/math] (элементы [math]r_{ij}[/math]), унитарная матрица [math]Q[/math] (элементы [math]q_{ij}[/math]).

Объём выходных данных: [math]\frac{n (n + 1)}{2} + n^2[/math] (в силу треугольности матрицы [math]R[/math] достаточно хранить только ее ненулевые элементы).

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Существует масса реализаций метода Грама-Шмидта без реортогонализации, о которых говорится, например, здесь. Про реализации с реортогонализацией информации нет.

3 Литература

<references \>

[[Категория:]]

[[Категория:]]