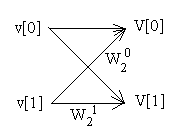Участник:Ivanov.kir.m/Быстрое дискретное преобразование Фурье: различия между версиями
Pumpkin (обсуждение | вклад) |
Pumpkin (обсуждение | вклад) |
||
| Строка 91: | Строка 91: | ||
void _fft(cplx *buf, cplx *out, int n, int step) | void _fft(cplx *buf, cplx *out, int n, int step) | ||
{ | { | ||
| − | + | if (step < n) { | |
| − | + | _fft(out, buf, n, step * 2); //рекурсивный рассчет | |
| − | + | _fft(out + step, buf + step, n, step * 2); | |
| − | + | for (int i = 0; i < n; i += 2 * step) { | |
| − | + | cplx t = cexp(-I * PI * i / n) * out[i + step]; | |
| − | + | buf[i / 2] = out[i] + t; | |
| − | + | buf[(i + n)/2] = out[i] - t; | |
| − | + | } | |
| − | + | } | |
} | } | ||
void fft(cplx *buf, int n) | void fft(cplx *buf, int n) | ||
{ | { | ||
| − | + | cplx out[n]; | |
| − | + | for (int i = 0; i < n; i++) out[i] = buf[i]; | |
| − | + | _fft(buf, out, n, 1); | |
} | } | ||
</source> | </source> | ||
Версия 22:55, 11 октября 2016
| Алгоритм Кули-Тьюки одномерного преобразования Фурье для действительных чисел | |
| Последовательный алгоритм | |
| Последовательная сложность | O (N \log N) |
| Объём входных данных | N действительных чисел |
| Объём выходных данных | \lfloor N/2 \rfloor+1 комплексных чисел |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O (\log N) |
| Ширина ярусно-параллельной формы | N |
Быстрое преобразование Фурье (БПФ, FFT) — алгоритм быстрого вычисления дискретного преобразования Фурье (ДПФ). То есть, алгоритм вычисления за количество действий, меньшее чем O(N^{2}), требуемых для прямого (по формуле) вычисления ДПФ. Иногда под БПФ понимается один из быстрых алгоритмов, называемый алгоритмом прореживания по частоте/времени или алгоритмом по основанию 2, имеющий сложность O(N\log(N)). Cуществует несколько различных алгоритмов для вычисления ДПФ считающимся быстрым преобразование Фурье:
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Рекурсивное описание
- 1.4 Вычислительное ядро алгоритма
- 1.5 Макроструктура алгоритма
- 1.6 Схема реализации последовательного алгоритма
- 1.7 Последовательная сложность алгоритма
- 1.8 Информационный граф
- 1.9 Ресурс параллелизма алгоритма
- 1.10 Входные и выходные данные алгоритма
- 1.11 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Одним из вариантов быстрого преобразования Фурье для вектора действительных чисел с размерностью равной степени двойки является алгоритм Кули-Тьюки. Отличительной особенностью данного алгоритма является то, что он обходится без использования специфических приемов, использующихся именно для степеней четверки, восьмерки и т.п. Однако благодаря тому, что на вход данному алгоритму подается вектор чисто вещественных чисел, выходной вектор удовлетворяет эрмитовой избыточности (Hermitian redundancy) , т.е. out[i] является сопряженным с out[n-i]. Это обстоятельство позволяет достичь роста скорости и снижения затрат памяти примерно в 2 раза по сравнению с комплексным аналогом алгоритма.
1.2 Математическое описание алгоритма
Входные данные: вектор действительных чисел a = (a_1,a_2,...,a_N).
Выходные данные: вектор комплексных чисел b = (b_1,b_2,...,b_{\lfloor N/2 \rfloor+1}).
Замечание: В простейшем случае алгоритм Кули-Тьюки применяется к векторам размерности степени двойки, поэтому на практике вектора иной размерности часто дополнять до ближайшей степени двойки. Такой подход делает алгоритм Кули-Тьюки не самым эффективным алгоритмом БПФ, поскольку дополнение до степени двойки может сильно усложнить задачу.
1.3 Рекурсивное описание
Алгоритм:
- Входной вектор a = (a_0,a_2,...,a_{N-1}) преобразуется в матрицу A размера n_1 \times n_2 , где N=n_1 \cdot n_2 и n_1 \lt n_2
A = \begin{pmatrix} a_0 & a_1 & \cdots & a_{n_1-1} \\ a_{n_1} & a_{n_1+1} & \cdots & a_{2n_1-1} \\ \vdots & \vdots & \ddots & \vdots \\ a_{(n_2-1)\cdot n_1} & a_{(n_2-1)\cdot n_1+1} & \cdots & a_{n_2\cdot n_1-1} \end{pmatrix}
- К каждой строке полученной матрицы применяется быстрое дискретное преобразование Фурье (БПФ) порядка n_1
- Каждый элемент полученный после применения БПФ умножается на поворотные множители exp (2 \pi i(m-1)(j-1)/N), где m - номер строки, а j - номер столбца
- Полученная после шагов 1-2 матрица A транспонируется
- К каждой строке матрицы A^T применяется БПФ порядка n_2
Замечание: Как правило все поворотные множители вычисляются заранее и хранятся в специальном массиве.
1.4 Вычислительное ядро алгоритма
В случае размерности входа равной степени двойки, вычислительным ядром алгоритма является, так называемая, "бабочка". В простейшем случае "бабочка" представляет из себя двухточечное преобразование. Рассмотрим этот случай:
На вход алгоритму подается двухэлементный вектор ‒ v = (v[0], v[1]) . Тогда для вычисления будут происходить по следующим формулам:
V[0] = W_2^0 v[0] + W_2^0 v[1] = v[0] + W_2^0 v[1]
V[1] = W_2^0 v[0] + W_2^1 v[1] = v[0] + W_2^1 v[1]
Данный процесс удобно изобразить с помощью следующей схемы:
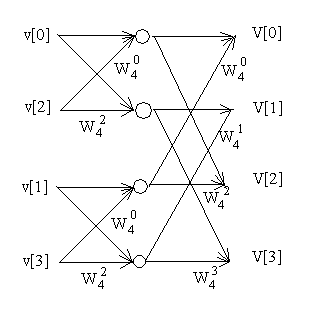
Для 4-х элеметного вектора v=(v[0],v[1],v[2],v[3]), алгоритм строится похожим образом. Сначала создаются простейшие "бабочки", а потом их результаты соединяются с противоположеной "бабочкой":
V[0]=v[0]+W_2^0 v[2]+W_4^0(v[1]+W_2^0 v[3])
V[1]=v[0]-W_2^0 v[2]+W_4^1(v[1]-W_2^0 v[3])
V[2]=v[0]+W_2^0 v[2]-W_4^0(v[1]+W_2^0 v[3])
V[3]=v[0]-W_2^0 v[2]-W_4^1(v[1]-W_2^0 v[3])
Схема в таком случае будет выглядеть следующим образом:
Для случая, когда вход не является степенью двойки, "бабочки" будут "несимментричными", но в остальном вычисления будут проходить схожим образом.
1.5 Макроструктура алгоритма
Для исходного вектора a = (a_1,a_2,...,a_N) размерности N = n_1 \cdot n_2, n_1 \lt n_2 БПФ представляется как:
- n_2 БПФ порядка n_1
- n_1 \cdot n_2 умножение комплексных чисел
- n_1 БПФ порядка n_2
1.6 Схема реализации последовательного алгоритма
Схема организации состоит в том, что на каждом шаге i для выполнения "бабочки" все элементы разбиваются на n_{i_1} векторов по n_{i_2} элементов, причем n_{i_1} \cdot n_{i_2} = n_i, где n_i длина входного вектора на текущем шаге i. В случае если такое разбиение невозможно, по причине того что n_i простое число, исходный вектор на текущем шаге дополняется элементом. В зависимости от номера шага, разница координат для каждой пары элементов увеличивается соразмерно разбиению (n_{i_1},n_{i_2}). При этом результат суммы записывается в элемент с меньшим номером, а результат вычитания с последующим умножением - в элемент с большим.
Простейший вариант алгоритма для степеней двойки на языке C:
#include <stdio.h>
#include <math.h>
#include <complex.h>
typedef double complex cplx;
void _fft(cplx *buf, cplx *out, int n, int step)
{
if (step < n) {
_fft(out, buf, n, step * 2); //рекурсивный рассчет
_fft(out + step, buf + step, n, step * 2);
for (int i = 0; i < n; i += 2 * step) {
cplx t = cexp(-I * PI * i / n) * out[i + step];
buf[i / 2] = out[i] + t;
buf[(i + n)/2] = out[i] - t;
}
}
}
void fft(cplx *buf, int n)
{
cplx out[n];
for (int i = 0; i < n; i++) out[i] = buf[i];
_fft(buf, out, n, 1);
}
1.7 Последовательная сложность алгоритма
Быстрое дискретное преобразование Фурье выполнимо за O(N(n_1+\cdots+n_m)) действий при N=n_1n_2\cdots n_m (в простом случае, при N=2^m необходимо O(N\log_2(N)) действий).Дискретное преобразование Фурье преобразует вектор a = (a_0, \dots, a_{N-1}) в вектор комплексных чисел b = (b_0, \dots, b_{N-1}), такой, что b_i=\sum_{j=0}^{N-1}a_j\varepsilon^{ij}, где \varepsilon^n=1 и \varepsilon^k\neq 1 при 0\lt k\lt N.
Основной шаг алгоритма состоит в сведении задачи для N чисел к задаче для n_1=N/n_2 числам, где n_2 — делитель N. Пусть мы уже умеем решать задачу для N/n_2 чисел. Применим преобразование Фурье к векторам a_i,a_{n_2+i}, \dots, a_{n_2(n_1-1)+i} для i=0,1,\dots,n_2-1. Покажем теперь, что за O(Np) действий можно решить исходную задачу. Заметим, что b_i=\sum_{j=0}^{n_2-1} \varepsilon^{ij} (\sum_{k=0}^{n_1-1}a_{kn_2+j}\varepsilon^{kin_2}). Выражения в скобках нам уже известны — это (i\pmod p)-тое число после преобразования Фурье j-го вектора. Таким образом, для вычисления каждого b_i нужно O(n_2) действий, а для вычисления всех b_i всего O(Nn_2) действий, что и требовалось.
В общем случае :
Пусть 4N\gt 2^k\ge2N. Заметим, что тогда b_i=\varepsilon^{-i^2/2}\sum_{j=0}^{N-1}\varepsilon^{(i+j)^2/2}\varepsilon^{-j^2/2}a_j. Обозначим \bar{a}_i=\varepsilon^{-i^2/2}a_i, \bar{b}_i=\varepsilon^{i^2/2}b_i, c_i=\varepsilon^{(2N-2-i)^2/2}. Тогда \bar{b}_i=\sum_{j=0}^{2N-2-i}\bar{a}_jc_{2N-2-i-j}, если положить \bar{a}_i=0 при i\ge N.
Таким образом задача сведена к вычислению свёртки, а это можно сделать с помощью трёх преобразований Фурье для 2^k элементов. Выполняем прямое преобразование Фурье для (\bar{a_0}, \cdots, \bar{a}_{2^k-1}) и (c_1,\cdots,c_{2^k-1}), перемножаем поэлементно результаты и выполняем обратное преобразование Фурье.
Вычисления всех \bar{a}_i и c_i требуют O(N) действий, три преобразования Фурье требуют O(N\log(N)) действий, перемножение результатов преобразований Фурье требует O(N) действий, вычисление всех b_i зная значения свертки требует O(N) действий. Итого для дискретного преобразования Фурье требуется O(N\log(N)) действий для любого N.
1.8 Информационный граф
1.9 Ресурс параллелизма алгоритма
Если считать только главные члены выражений, то простой алгоритм Кули-Тьюки имеет критический путь, состоящий из log(N) операций комплексного сложения/вычитания и log(N) операций комплексного умножения (основание log целиком зависит от выбранного на каждом шаге алгоритма разбиения). Таким образом, простой алгоритм БПФ в общем случае может быть отнесён к логарифмическому классу по параллельной сложности.
1.10 Входные и выходные данные алгоритма
Входные данные: вектор действительных чисел a = (a_1,a_2,...,a_N).
Выходные данные: вектор комплексных чисел b = (b_1,b_2,...,b_{\lfloor N/2 \rfloor+1}).
1.11 Свойства алгоритма
Таким образом в общем у алгоритма БПФ в случае неограниченных ресурсов:
- последовательная сложность - линейно-логарифмическая
- параллельная сложность - логарифмическая.
При этом алгоритм полностью детерминирован.
2 ЧАСТЬ. Программная реализация алгоритма
В качестве тестируемой реализации была выбрана библиотека FFTW, а именно функция, выполняющая БПФ одномерного вектора действительных чисел.
2.1 Масштабируемость алгоритма и его реализации
2.2 Существующие реализации алгоритма
Наиболее известной библиотекой для выполнения различных вариантов быстрого преобразования Фурье является FFTW, разработанная Матео Фриго и Стивеном Джонсоном в Массачусетском технологическом институте. Для преобразования небольших объемов данных используется алгоритм Кули - Тьюки, в случае входа больших размеров используется алгоритм Радера или Блюштейна. Библиотека считается самой быстрой реализацией БПФ и на входах любых размеров и размерностей сохраняет ассимптотическую сложность O(N\cdot log(N)). Также, существует версия FFTW с поддержкой MPI, которая позволяет с объемами данных не умещающимися в память.
FFTW изначально написана на языке C, однако имеет API для нескольких языков, в том числе Fortran и Ada. Открытая версия библиотеки распространяется под лицензией GNU General Public License. Также существует реализация для коммерческого использования распространяемая под лицензией MIT.
Существует несколько реализаций алгоритма, для рассчета на GPU:
3 Литература
[1] Википедия [Электронный ресурс]. Тема: Быстрое преобразование Фурье – Электрон. дан. – URL Быстрое преобразование Фурье (дата обращения 17.09.2016)