Участник:ЕкатеринаКозырева/Алгоритм динамической иерархической кластеризации CHAMELEON

Алгоритм динамической иерархической кластеризации CHAMELEON
Последовательный алгоритм
Последовательная сложность	$O(nm + n log n + m^2 log m)$
Объём входных данных	$\frac{n (n - 1)}{2}$
Объём выходных данных	$n$
Параллельный алгоритм
Высота ярусно-параллельной формы
Ширина ярусно-параллельной формы

Автор описания Е.А.Козырева

1 часть. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм CHAMELEON был предложен в 1999 году тремя учеными из университета Миннесоты – George Karypis, Eui-Hong (Sam) Han и Vipin Kumar[1].

Предназначен для решения задач кластеризации. Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны.

CHAMELEON - это агломеративный иерархический алгоритм кластеризации, ключевой особенностью которого является то, что он учитывает и взаимную связность, и сходство при определении наиболее похожей пары подкластеров, основываясь на динамической модели. Это означает, что в процессе кластеризации два кластера объединяются, только если их относительная взаимная связность и относительное взаимное сходство являются высокими по отношению к внутренней взаимосвязанности кластеров и близости элементов внутри кластеров. Кроме того, Хамелеон использует подход для моделирования степени взаимосвязанности и близости между каждой парой кластеров, который учитывает внутренние характеристики самих кластеров. Таким образом, он может автоматически адаптироваться к внутренним характеристикам объединяемых кластеров.

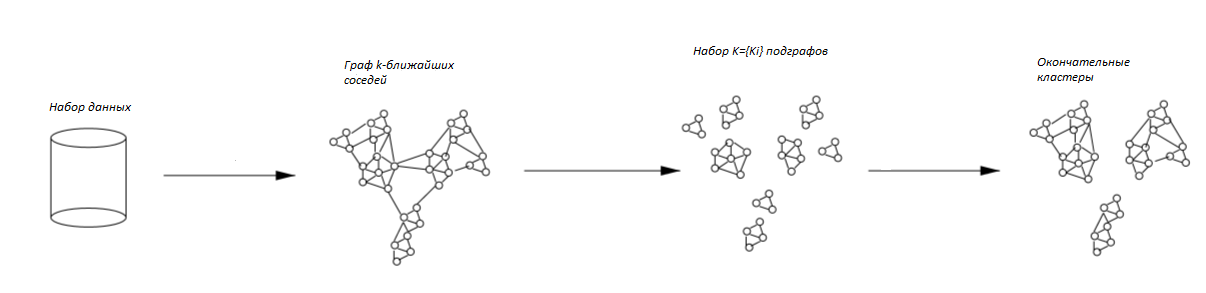
CHAMELEON находит кластеры в наборе данных с помощью трехфазного алгоритма. На первой фазе происходит построение графа, путём добавления рёбер по принципу k ближайших соседей. На второй фазе CHAMELEON группирует полученные элементы в множество относительно небольших подкластеров. Во время третьей фазы применяется агломеративный иерархический алгоритм кластеризации, с помощью которого находятся естесственные кластеры путем многократного объединения подкластеров, полученных на прошлом этапе.

1.2 Математическое описание алгоритма

Исходные данные:

• Множество из n точек $V= {v_{ij}}$ в метрическом пространстве, которое задано симметрической матрицей расстояний $A$ размера $n\times n$.
• $k$ - количество ближайших соседей для вершин, $k \in N, k \leq n$.
• $l$ - наименьшее число вершин, которое может содержать наибольший подграф на 2-м этапе, $l \in N, l \leq n$.

Обозначения:

• $G = (V, E)$ - граф, полученный путём соединения каждой точки с её $k$ ближайшими соседями.

• $K= \{K_{i}\}$ - разбиение множества V на набор попарно непересекающихся связных подмножеств, полученное в результате выполнения второй фазы алгоритма.

• $G_{2} = (K, E_{2})$ - взвешенный граф, вершинами которого являются получившиеся подграфы, а ребрами - количество ребер исходного графа, соединяющих соответствующие подграфы.

• $C = \{C_{i}\}$ - итоговое разбиение множества вершин графа $G_{2}$ на набор кластеров.

Вспомогательные понятия

• $EC_{(C_{i},C_{j})}$ - абсолютная взаимная связность пары кластеров $C_{i}, C{j}$. Определяется как сумма весов ребер, соединяющих вершины, принадлежащие $C{i}$ c вершинами из $C{j}$. Внутренняя связность $EC_{(C_{i},C_{i})}$ вычисляется как сумма ребер, входящих в разделитель, разбивающий $C{i}$ на два равных подграфа.

• $RI_{(C_{i},C_{j})} = \frac{|EC_{(C_{i},C_{j})}|}{(|EC_{C_{i}}|+|EC_{C_{j}}|)/2}$ - относительная взаимная связность пары кластеров $C_{i}, C{j}$

• $S_{EC_{(C_{i},C_{j})}}$ - абсолютное взаимное сходство пары кластеров $C_{i}, C{j}$. Подсчитывается как среднее сходство между соединенными вершинами, принадлежащими $C{i}$ и $C{j}$ соответственно. Соединения обусловлены разбиением общего графа, полученного на первом этапе алгоритма.

• $RC_{(C_{i},C_{j})}= \frac{S_{EC_{(C_{i},C_{j})}}}{\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{i})}}+\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{j})}}}$ - относительное взаимное сходство пары кластеров $C_{i}, C{j}$. Определяется как абсолютное сходство между этой парой кластеров, нормализованное с учетом их внутреннего сходства.

Первый этап

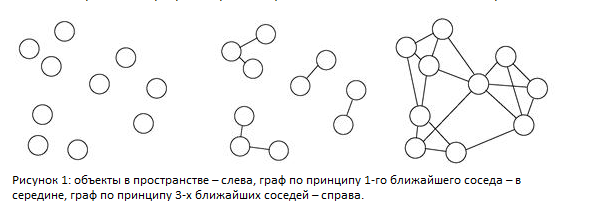
На первом этапе, согласно графо-ориентированному подходу, происходит построение графа $G = (V, E)$ на матрице сходства объектов по принципу k ближайших соседей. Две вершины такого графа соединяет ребро, если объект, соответствующий любой из этих вершин попадает в число k наиболее близких объектов для объекта, соответствующего другой вершине из данной пары.

Второй этап

Алгоритм разделяет полученный граф на множество сравнительно малых подграфов $K= \{K_{i}\}$. Разделение происходит последовательно. На каждом шаге выбирается подграф, содержащий наибольшее число вершин. Этот граф разделяется на два подграфа так, что разделитель ребер графа минимален и каждый из получаемых подграфов содержит не менее 25 % вершин исходного графа. Процесс разделения останавливается, когда наибольший подграф содержит меньше некоторого заданного числа вершин. Обычно величина этого параметра задается равной значению от 1 до 5 % от числа объектов. Полученное множество связных графов считается множеством начальных кластеров, на котором требуется провести последовательное иерархическое объединение.

Третий этап

Третий этап заключается в итеративном преобразовании множества подграфов $K= \{K_{i}\}$ в множество кластеров $C = \{C_{i}\}$. Алгоритм осуществляет агломеративную иерархическую кластеризацию на основании показателей $EC_{(C_{i},C_{j})}$, $S_{EC_{(C_{i},C_{j})}}$, $RI_{(C_{i},C_{j})}$, $RC_{(C_{i},C_{j})}$. Существует две стратегии анализа показателей сходства. Первая подразумевает наличие некоторых пороговых значений $T_{RI}$ и $T_{RC}$. В соответствии с этой стратегией, алгоритм для каждого кластера $C_{i}$ проверяет, отвечают ли смежные (наиболее близкие) ему кластеры условиям:

• $RI_{(C_{i},C_{j})} \geqslant T_{RI}$

• $RC_{(C_{i},C_{j})} \geqslant T_{RC}$

Если более одного смежного кластера отвечает этим условиям, то алгоритм выбирает для объединения наиболее связный кластер (граф), то есть такой кластер $C_{j}$, с которым у кластера $C_{i}$ получается наибольшая абсолютная взаимная связность. По завершению прохода по всем кластерам, созданные таким образом пары объединяются. Параметры $T_{RI}$ и $T_{RC}$ могут использоваться для изменения характеристик получаемых кластеров.

Вторая стратегия заключается в использовании специальной функции, объединяющей понятия относительной взаимной связности и относительного взаимного сходства. На каждом шаге выбираются те кластеры для объединения, которые максимизируют эту функцию:

$RI_{(C_{i},C_{j})}*RC_{(C_{i},C_{j})}^\alpha$,

где $\alpha$ выбирается пользователем. Если $\alpha \gt 1$, то алгоритм придает большее значение относительному взаимному сходству, а если $\alpha \lt 1$, то большее значение имеет относительная взаимная связность.

Вычисляемые данные:

$U = (u_1, u_2, ..., u_n)$ - n-мерный вектор, где $u_i \in N_{[C]}$ - порядковый номер кластера, к которому принадлежит вершина i исходного множества V.

1.3 Вычислительное ядро алгоритма

Алгоритм имеет три вычислительных ядра, по одному на каждый этап.

На первом этапе вычислительным ядром является процесс нахождения $k$ ближайших соседей для каждой вершины, который заключается в анализе матрицы расстояний.

На втором этапе вычислительным ядром является процесс поиска подходящего разбиения очередного подграфа на два графа с минимизацией разделителя ребер графа.

На третьем этапе вычислительным ядром является расчет величин $EC_{(C_{i},C_{j})}$, $S_{EC_{(C_{i},C_{j})}}$, $RI_{(C_{i},C_{j})}$, $RC_{(C_{i},C_{j})}$ для каждой пары смежных кластеров.

1.4 Макроструктура алгоритма

Как уже рассказывалось ранее, алгоритм включает в себя три основных этапа, каждый из которых, по сути, является отдельным алгоритмом. Этапы выполняются последовательно относительно друг друга.

Макрооперация на первом этапе - процедура нахождения $k$ ближайших соседей, на втором - процедура разбиения наибольшего подграфа на два графа, на третьем - процедура вычисления показателей сходства, на основе которых принимается решение о слиянии подграфов в кластер.

1.9 Входные и выходные данные алгоритма

Входные данные

1. Симметрическая матрица $A$ расстояний между элементами данных размера $n\times n$ с нулями на главной диагонали ($a_{ii}= 0, i = 1, \ldots, N$).

2. $k$ - количество ближайших соседей для вершин (рекомендуемое значение $k$ от 5 до 20 в зависимости от количества анализируемых объектов).

3. $l$ - наименьшее число вершин, которое может содержать наибольший подкластер на 2-м этапе . Величина этого параметра варьируется от 1 до 5 % от общего числа объектов.

Объём входных данных

$\frac{n (n - 1)}{2}$ (в силу симметричности и нулевой главной диагонали достаточно хранить только над/поддиагональные элементы).

Выходные данные

Вектор из $n$ чисел $u_{1}, u_{2}, \ldots, u_{N}$, где $u_{i}$ - целое число, соответствующее кластеру $i$-го объекта.

Объём выходных данных

$n$

3 Литература

[1] George Karypis, Eui-Hong (Sam) Han и Vipin Kumar, «Chameleon: Hierarchical Clustering Using Dynamic Modeling», 1999.

[2] http://studopedia.ru/7_41934_algoritm-dinamicheskoy-ierarhicheskoy-klasterizatsii-CHAMELEON.html