Участник:Sagak/Алгоритм Ланцоша в арифметике с плавающей точкой

1 Алгоритм Ланцоша

Алгоритм Ланцоша – итерационный метод , созданный Корнелиусом Ланцошем, для нахождения собственных значений и собственных веторов симметричной матрицы. Суть алгоритма в том, что он сводит частичную проблему собственных значений симметричной вещественной матрицы к полной проблеме собственных значений для симметричной трехдиагональной матрицы меньшей размерности. Алгоритм применяется к матрицам большой размерности, к которым не применимы никакие прямые методы. Есть три вида алгоритма: Алгоритм Ланцоша с точной арифметикой, Алгоритм Ланцоша в арифметике с плавающей точкой и Алгоритм Ланцоша с выборочной ортогонализацией. Алгоритм Ланцоша в арифметике с плавающей точкой учитывает округления, возникающие при вычислениях.

Симметричность матрицы позволяет хранить и вычислять только чуть больше половины её элементов, что почти вдвое экономит как необходимые для вычислений объёмы памяти, так и количество операций.Также алгоритм позволяет использовать так называемый режим накопления, обусловленный тем, что значительную часть вычислений составляют вычисления скалярных произведений.

2 Математическое описание алгоритма

Исходные данные: положительно определённая симметрическая матрица [math]A[/math], вектор [math]b[/math],количество итераций [math]k[/math].

Вычисляемые данные: трехдиагональная матрица [math]T_k[/math](элементы [math]t_{ij}[/math]) размерности [math]k[/math].

Формула метода:

[math] \begin{align} q_1&=b/||b||,\beta_0=0,q_o=0. \\ z&=Aq_j, \\ \alpha_j&=q_j^Tz, \\ z& =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, \\ \end{align} [/math]

[math] \begin{align} \\ z&=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, \\ z&=z-\alpha_jq_j-\beta_{j-1}q_{j-1}, \\ \beta&=||z||,\\ q_{j+1}&=z/\beta_j, \quad j \in [1, k]. \end{align} [/math]

Полная переортогонализация соответствует повторному проведению операции [math]z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i,[/math], для того чтобы почти гарантировать, что z будет ортогонален векторам [math]q_1...q_{j-1}[/math].

3 Вычислительное ядро алгоритма

Вычислительное ядро последовательной версии алгоритма Ланцоша можно составить из операции умножения вектора на матрицу и процесса полной переортогонализации, именно на них приходится основное время работы алгоритма.

• 1. [math]Aq=( \sum\nolimits_{i=^n}a_{1i}q_i, \sum\nolimits_{i=2}^na_{2i}q_i, ..., \sum\nolimits_{i=1}^na_{ni}q_i)[/math], как известно в операции задействуется [math]n^2[/math] умножений и [math]n(n-1)[/math]сложений.

• 2. [math]z=z-\sum\nolimits_{i=1}^{k}(z^Tq_i)q_i, z=z-\sum\nolimits_{i=1}^{k}(z^Tq_i)q_i,[/math] сложность переортогонализации:[math]k(k+1)n+2k[/math] умножений и [math]k(k+1)n+2+k[/math] сложений.

4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют множественные вычисления скалярных произведений

[math](x,y)=\sum\nolimits_i^nx_iy_i[/math]

5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая:

[math] \begin{align} \\ 1 .& q_1=b/||b||,\\ 2 .& \beta_0=0,\\ 3 .&q_o=0. \\ \end{align} [/math]

Далее для всех [math]j[/math] от [math]1[/math] до [math]k[/math] по нарастанию выполняются

[math] \begin{align} 4&.z=Aq_j, \\ 5&.\alpha_j=q_j^Tz, \\ 6&.z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, \\ 7&.z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, \\ 8&.z=z-\alpha_jq_j-\beta_{j-1}q_{j-1}, \\ 9&.\beta=||z||,\\ 1&0.q_{j+1}=z/\beta_j.\\ \end{align} [/math]

При этом если [math]\beta=0[/math], то алгоритм завершается.

6 Последовательная сложность алгоритма

Для выполнения алгоритма Ланцоша в последовательном варианте требуется:

• [math]k[/math] вычислений квадратного корня,

• [math]k((n+1)^2+nk-1)[/math] сложений (вычитаний),

• [math]k((n+1)^2+2kn)[/math] умножений

Умножения и сложения (вычитания) составляют основную часть алгоритма.

7 Информационный граф

Опишем граф алгоритма в виде рисунка.

• Вершина черного цвета соответствует операции [math]Aq_j,[/math].
• Вершина красного цвета соответствует операции скалярного произведения [math]q_j^Tz[/math].
• Вершина сиреневого цвета соответствует операции [math]z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i[/math].
• Вершина желтого цвета соответствует операции [math]z-\alpha_jq_j-\beta_{j-1}q_{j-1}[/math].
• Вершина синего цвета соответствует операции [math]||z||[/math].
• Вершина зеленого цвета соответствует операции [math]z/\beta_j[/math].

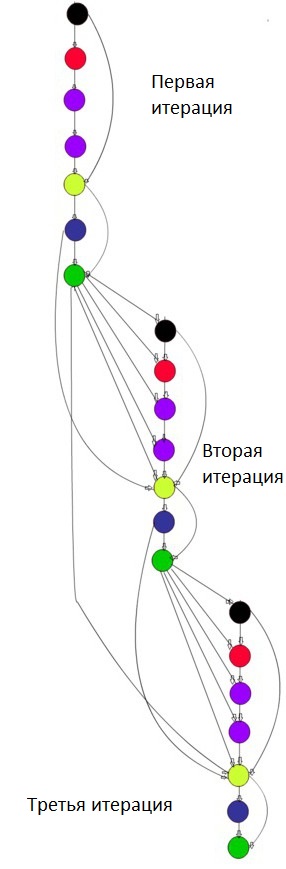Здесь показаны первые три итерации алгоритма,при больших итерациях граф строится аналогичным образом.

Отметим, что можно подробнее расписать первые четыре операции, в первая из них является стандартной операцией умножения вектора на матрицу,вторая-скалярное произведение, третье-сумма скалярных произведений. Именно эти операции содержат ресурс параллелизма.

8 Ресурс параллелизма алгоритма

Как видно из графа алгоритма каждая операция передает результат своих вычислений последующей операции. Соответственно никаких ресурсов параллелизма на уровне взаимодействия этих базовых операции нету. Они могут выполнятся строго последовательно. Однако, шесть операций содержат вычисления множества скалярных произведений.Стоит отметить, что в каждой итерации есть операция умножения матрицы на вектор, что представляет из себя [math]n[/math] информационно независимых скалярных произведений. Также хорошие возможности для параллельной реализации представляет повторная переортогонализация, так как на [math]j[/math] итерации обе операции ортогонализации вычисляют [math]j-1[/math] независимых скалярных произведения. Поскольку каждое вычисление скалярного произведения векторов длины [math]n[/math] требует выполнения [math]n[/math] операций умножения и [math]n-1[/math] операций сложения, его сложность [math]n[/math]. Если воспользоваться разделением данных по строкам, то в случае параллельных вычислений каждый процессор производит умножение только части (полосы) первого вектора на второй, размер этих полос равен [math]n/p[/math]

([math]p[/math]-количество процессоров). Следовательно, вычислительная сложность параллельного алгоритма скалярного произведения определяется выражением:[math]n/p[/math], а мультипликативная сложность всего алгоритма [math]O(n^2k+nk^2)/p)[/math]. При p=n получаем [math]O(nk+k^2)[/math]. Однако этот метод не учитывает, то что есть скалярные произведения, которые могут вычисляться параллельно. Если учесть весь ресурс параллелизма можно получить сложность [math]O(k)[/math].

9 Входные и выходные данные алгоритма

Входные данные: плотная матрица [math]A[/math] (элементы [math]a_{ij}[/math]),произвольный вектор [math]b[/math], количество итераций [math]k[/math].

Дополнительные ограничения:

• [math]A[/math] – симметрическая матрица, т. е. [math]a_{ij}= a_{ji}, i, j = 1, \ldots, n[/math]..

Объём входных данных: [math]\frac{n (n + 3)}{2}[/math] (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы).

Выходные данные: трехдиагональная симметрическая матрица [math]T[/math] (элементы [math]_{ij}[/math]), либо два вектора [math]a[/math] и [math]b[/math] размерности [math]k[/math].

Объём выходных данных: [math]2k[/math] (в силу трехдиагональности симметричности достаточно хранить только ненулевые элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом.

10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов равняется [math]O(n^2)[/math]. При этом вычислительная мощность алгоритма умножения матриц, как отношение числа операций к суммарному объему входных и выходных данных [math]O(k)[/math].Алгоритм не детерминированный, так как если в какой-то итерации [math]b_j=0[/math], то алгоритм останавливается. Также на недетерминированность может повлиять изменение порядка выполнения ассоциативных операций. Для уменьшения ошибок округления режимом накопления в ряде алгоритмов, использующих скалярное произведение одинарной точности, оно вычисляется с двойной точностью.