Участник:Danyanya/Алгоритм Ланцоша для точной арифметики (без переортогонализации)

Алгоритм Ланцоша для точной арифметики (без переортогонализации)
Последовательный алгоритм
Последовательная сложность	$O(kn^2)$
Объём входных данных	$\frac{n(n + 1)}{2}$
Объём выходных данных	$k(n + 1)$
Параллельный алгоритм
Высота ярусно-параллельной формы	$O(k)$
Ширина ярусно-параллельной формы	$O(n^2)$

Основные авторы описания: Д.Р.Слюсарь

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша поиска собственных значений был опубликован Корнелием Ланцошем в 1950 году [1]. Этот итерационный алгоритм применим только к эрмитовым матрицам $A$. Метод позволяет за $k$ итераций вычислять $k$-ое приближение собственных значений и собственных векторов исходной матрицы $A$.

В данной статье рассмотрен упрощенный вариант алгоритма Ланцоша, подразумевающие отсутствие влияния ошибок округления на вычислительный процесс.

Данный алгоритм является неустойчивым, вследствие чего на практике применяется модифицированный алгоритм Ланцоша с полной переортогонализацией.

1.2 Математическое описание алгоритма

На вход алгоритма подается эрмитова матрица $A = A^\dagger$ (в вещественном случае - симметрическая) ,

$A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1\ n-1} & a_{1\ n} \\ a_{12} & a_{22} & a_{23} & \cdots & a_{2\ n-1} & a_{2\ n} \\ a_{13} & a_{23} & a_{33} & \cdots & a_{3\ n-1} & a_{3\ n} \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ a_{1\ n-1} & \cdots & \cdots & a_{n-2\ n-1} & a_{n-1\ n-1} & a_{n-1\ n} \\ a_{1\ n} & \cdots & \cdots & a_{n-2\ n} & a_{n-1\ n} & a_{n\ n} \\ \end{pmatrix}$

Алгоритм Ланцоша соединяет в себя метод Ланцоша построения крыловского подпространства с процедурой Релея-Ритца. Иными словами, из оргонормированных векторов Ланцоша [??] на каждой итерации строится матрица $Q_k = [q_1, q_2, \dots, q_k]$ размерности $n \times k$. В качестве приближенных собственных значений матрицы $A$ берутся числа Ритца, т.е. собственные значения симметричной трехдиагональной матрицы $T_k = Q^T_k A Q$:

$T_k = \begin{pmatrix} \alpha_1 & \beta_1 & 0 & \dots & 0 \\ \beta_1 & \alpha_2 & \beta_2 & \dots & 0 \\ 0 & \beta_2 & \ddots & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & \beta_{k-1} \\ 0 & \dots & \dots & \beta_{k-1} & \alpha_k \end{pmatrix}$

1.3 Вычислительное ядро алгоритма

Вычислительным ядром на каждой итерации является вычисление произведения исходной матрицы $A$ на вектор $q_i$ с предыдущей итерации

$z = Aq_i$

1.4 Макроструктура алгоритма

Макрооперациями в алгоритме являются:

• Процедура иттеративного построения трехдиагональной симметричной матрицы, включающая:
  • умножение матрицы на вектор;
  • скалярное произведение векторов;
  • деление (умножение) вектора на вещественное число;
• Вычисление собственного значение и собственных векторов полученной в ходе работы трехдиагональной симметричной матрицы.

1.5 Схема реализации последовательного алгоритма

Исходные данные: симметричная матрица $A$, случайный вектор $b$.

Вычисляемые данные: собственные вектора матрицы $T_k$ являющиеся столбцами матрицы $Q_k V$, и матрица собственных значений $\Lambda$, где $V, \Lambda$ из спектрального разложения $T_k = V\Lambda V^T$.

Алгоритм на псевдокоде:

$\begin{align} q_1 = & b/ \|b\|_2,\; \beta_0 = 0,\; q_0 = 0\\ for \; & i = 1 \; to \; k \\ & z = Aq_i\\ & \alpha_i = q^T_i z\\ & z = z - \alpha_i q_i - \beta_{i-1}q_{i-1}\\ & \beta_i = \|z\|_2\\ & If \; \beta_i == 0 \; then \\ & \; \; \; \; exit\\ & else \\ & \; \; \; \; q_{i+1} = z / \beta_i \\ end \; & for \end{align}$

После этого вычисляются собственные значения и собственные вектора симметричной трехдиагональной матрицы $T_k$ наиболее удобным образом.

1.6 Последовательная сложность алгоритма

Последовательная сложность алгоритма рассчитана на основе приведенной выше реализации алгоритма. Исходя из псевдокода последовательно выполняются следующие операции:

• Умножение квадратной матрицы $n * n$ на вектор длины $n$. Требует $n * n$ умножений и сложений;
• Скалярное произведение векторов длины $n$. Требует $n$ умножений и сложений;
• Сложение векторов длины $n$. Требует $n$ сложений;
• Умножение вектора длины $n$ на скаляр. Требует $n$ умножений;
• Нахождение квадратичной нормы вектора длины $n$. Требует $n$ умножений и сложений + извлечения квадратного корня;
• Нахождение собственных значений и векторов трехдиагональной симметричной матрицы размера $k \times k$. Наиболее эффективный метод метода «Разделяй-и-властвуй» в среднем требует $~O(k^{2.3})$ операций.

Таким образом, в худшем случае, алгоритм Ланшоца имеет сложность $O(k * n^2)$ и односится к квадратичным алгоритмам.

1.7 Информационный граф

Информационный граф алгоритма можно разбить на две части:

• Общий граф алгоритма, от входа IN до функции вычислений собственных значений полученной трехдиагональной матрицы (EIGEN) (Рис. 1);

Общий граф алгоритма. IN - вход, Iter - одна итерация алгоритма, EIGEN - процедура вычисления собственных значений

• Подграф на каждой итерации внутри цикла (от IN до NEXT в рисунке 2);

Подграф алгоритма, описывающий одну итерацию. IN - вход в очедедную итерацию, NEXT - переход к следующей итерации или выход цикла, между ними возможен параллелизм при операциях умножения/сложения, вычитания из q(i) q(i-1)-ого, а также деления нового вектора на норму (полученную в блоке Norm). Красными стрелками показаны переходы в непараллельные секции (переход в NEXT неизбежен, из-за чего помечен зеленым)

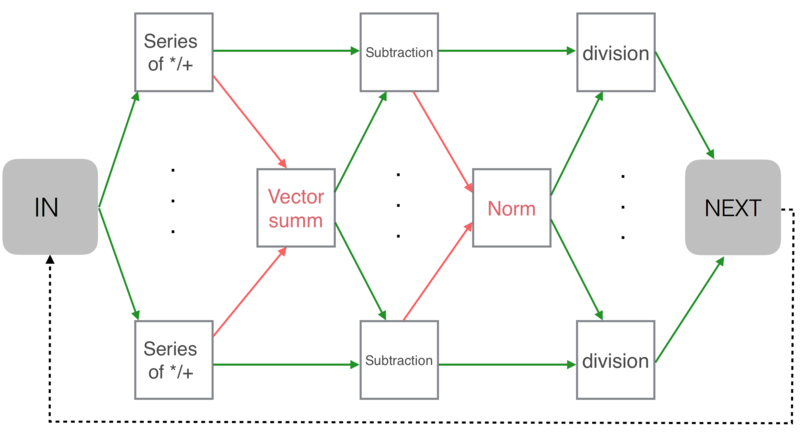
1.8 Ресурс параллелизма алгоритма

Важно заметить, что итерации алгоритма выполняются строго последовательно, а распараллеливание возможно только внутри итераций.

1.9 Входные и выходные данные алгоритма

Входные данные: симметричная вещественная матрица $A$, случайный вектор $b$, число итераций $k$.

Объём входных данных: $n * (n + 1) + 1$.

Выходные данные: вектор собственных значений $\Lambda$, матрица собственных векторов $E$.

Объём выходных данных: $k * (n + 1)$.

1.10 Свойства алгоритма

• Алгоритм Ланцоша без переортогонализации не является детерминированным из-за того, что возможно выполнение меньшего числа итераций алгоритма, из-за того, что все собственные значения уже вычислены;

• Также алгоритм Ланцоша быстро сходится при вычислении собственных значений матрицы $A$, находящихся на границе ее спектра (в $T_{j}$ в первую очередь появляются максимальные по модулю собственные значения).

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

TDB next week

2.7 Существующие реализации алгоритма

В настоящее время существует множество реализаций алгоритма Ланцоша итеративного поиска собственных значений, как входящих в официальные дистрибутивы для вычислений (ARPACK), так и неофициальных реализаций, выложенных на Github. Среди них:

1. The IETL Project [2]

2. MatLab [3]

3. ARPACK [4]

4. Julia Math [5]

...

3 Литература

1. Алгоритм Ланцоша (Википедия) [6]

2. Деммель Д. Вычислительная линейная алгебра/Пер. с англ. ХД Икрамова. – 2001.