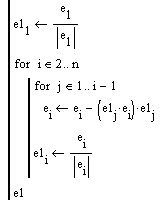Участник:DVIN/Ортогонализация Грамма-Шмидта

Эта работа ждет рассмотрения преподавателем
Дата последней правки страницы: 15.10.2016
Авторы этой статьи считают, что задание выполнено.

Ортогонализация Грама-Шмидта
Последовательный алгоритм
Последовательная сложность	$O(n^3)$
Объём входных данных	$n^2$
Объём выходных данных	$n^2$
Параллельный алгоритм
Высота ярусно-параллельной формы	$O(n)$
Ширина ярусно-параллельной формы	$O(n^2)$

Основные авторы описания: Инжелевская Дарья Валерьевна

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Создатели алгоритма Эрхард Шмидт и Йорген Педерсен Грам.

Эрхард Шмидт (14 января 1876 — 6 декабря 1959) — немецкий математик, с 1917 года профессор Берлинского университета. В 1946—58 первый директор Института математики АН ГДР. Основные труды по теории функций, интегральным уравнениям, функциональному анализу. Определил и изучил геометрически гильбертово пространство, используя аналогии с геометрией Евклида. Занимался квадратичными формами. Известен оператор Гильберта-Шмидта и процесс Грама ― Шмидта.

Йорген Педерсен Грам (27 июня 1850 - 29 апреля 1916) датский математик, родился в герцогстве Шлезвиг, Дания и умер в Копенгагене, Дания. Основные его работы "On series expansions determined by the methods of least squares", "Investigations of the number of primes less than a given number". Математический метод, который носит его имя, процесс Грама-Шмидта, впервые был опубликован в 1883. Теорема Грама и Определитель Грама также назван в его честь.

Процесс Грама-Шмидта — это один из алгоритмов, в которых на основе счётного множества линейно независимых векторов $\mathbf {a} _{1},\;\ldots ,\;\mathbf {a} _{N}$ строится множество ортогональных векторов $\mathbf {b}_{1},\;\ldots ,\;\mathbf {b} _{N}$ или ортонормированных векторов $\mathbf {e} _{1},\;\ldots ,\;\mathbf {e}_{N}$ , причём так, что каждый вектор $\mathbf {b} _{j}$ или $\mathbf {e} _{j}$ может быть выражен линейной комбинацией векторов $\mathbf {a} _{1},\;\ldots ,\; \mathbf {a} _{j}$ .

1.2 Математическое описание алгоритма

1.2.1 Классический процесс Грама — Шмидта

1.2.1.1 Алгоритм

Пусть имеются линейно независимые векторы $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_N$ .

Определим оператор проекции следующим образом: $\mathbf{proj}_{\mathbf{b}}\,\mathbf{a} = {\langle \mathbf{a}, \mathbf{b} \rangle \over \langle \mathbf{b}, \mathbf{b}\rangle} \mathbf{b} ,$

где $\langle \mathbf{a}, \mathbf{b} \rangle$ — скалярное произведение векторов $\mathbf{a}$ и $\mathbf{b}$ .

Скалярное произведение для двух векторов $\mathbf{ a= [a_1, a_2, ...,a_k]}$ и $\mathbf{ b= [b_1, b_2, ..., b_k]}$ в k-мерном действительном пространстве определяется как:

$\mathbf{a}\cdot\mathbf{b}=\sum_{i=1}^k a_ib_i=a_1b_1+a_2b_2+\cdots+ a_kb_k$ .

Этот оператор проецирует вектор $\mathbf{a}$ коллинеарно вектору $\mathbf{b}$ .

Ортогональность векторов $\mathbf{a}$ и $\mathbf{b}$ достигается на шаге (2).

Классический процесс Грама — Шмидта выполняется следующим образом:

${\begin{array}{lclr} {\mathbf {b}}_{1}&=&{\mathbf {a}}_{1}&(1)\\ {\mathbf {b}}_{2}&=&{\mathbf {a}}_{2}-{\mathbf {proj}}_{{{\mathbf {b}}_{1}}}\,{\mathbf {a}}_{2}&(2)\\ {\mathbf {b}}_{3}&=&{\mathbf {a}}_{3}-{\mathbf {proj}}_{{{\mathbf {b}}_{1}}}\,{\mathbf {a}}_{3}-{\mathbf {proj}}_{{{\mathbf {b}}_{2}}}\,{\mathbf {a}}_{3}&(3)\\ {\mathbf {b}}_{4}&=&{\mathbf {a}}_{4}-{\mathbf {proj}}_{{{\mathbf {b}}_{1}}}\,{\mathbf {a}}_{4}-{\mathbf {proj}}_{{{\mathbf {b}}_{2}}}\,{\mathbf {a}}_{4}-{\mathbf {proj}}_{{{\mathbf {b}}_{3}}}\,{\mathbf {a}}_{4}&(4)\\ &\vdots &&\\{\mathbf {b}}_{N}&=&{\mathbf {a}}_{N}-\displaystyle \sum _{{j=1}}^{{N-1}}{\mathbf {proj}}_{{{\mathbf {b}}_{j}}}\,{\mathbf {a}}_{N}&(N) \end{array}}$

На основе каждого вектора $\mathbf{b}_j \;(j = 1 \ldots N)$ может быть получен нормированный вектор: $\mathbf{e}_j = {\mathbf{b}_j\over \| \mathbf{b}_j \|}$ (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).

Результаты процесса Грама — Шмидта:

$\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N$ — система ортогональных векторов либо

$\mathbf{e}_1,\;\ldots,\;\mathbf{e}_N$ — система ортонормированных векторов.

Вычисление $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N$ носит название ортогонализации Грама — Шмидта, а $\mathbf{e}_1,\;\ldots,\;\mathbf{e}_N$ — ортонормализации Грама — Шмидта.

1.2.1.2 Доказательство

Докажем ортогональность векторов $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_N$ .

Для этого вычислим скалярное произведение $\langle \mathbf{b}_1, \mathbf{b}_2 \rangle$ , подставив в него формулу (2). Мы получим ноль. Равенство нулю скалярного произведения векторов означает, что эти векторы ортогональны. Затем вычислим скалярное произведение $\langle \mathbf{b}_1, \mathbf{b}_3 \rangle$ , используя результат для $\langle \mathbf{b}_1, \mathbf{b}_2 \rangle$ и формулу (3). Мы снова получим ноль, то есть векторы $\mathbf{b}_1$ и $\mathbf{b}_3$ ортогональны. Общее доказательство выполняется методом математической индукции.

1.2.1.3 Геометрическая интерпретация — вариант 1

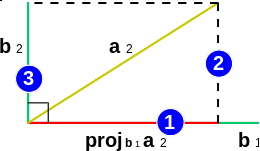
Рис. 1. Второй шаг процесса Грама — Шмидта

Рассмотрим формулу (2) — второй шаг алгоритма. Её геометрическое представление изображено на рис. 1:

1 — получение проекции вектора $\mathbf{a}_2$ на $\mathbf{b}_1$ ;

2 — вычисление $\mathbf{a}_2-\mathbf{proj}_{\mathbf{b}_1}\mathbf{a}_2$ , то есть перпендикуляра, которым выполняется проецирование конца $\mathbf{a}_2$ на $\mathbf{b}_1$ .

Этот перпендикуляр — вычисляемый в формуле (2) вектор $\mathbf{b}_2$ ;

3 — перемещение полученного на шаге 2 вектора $\mathbf{b}_2$ в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (2).

На рисунке видно, что вектор $\mathbf{b}_2$ ортогонален вектору $\mathbf{b}_1$ , так как $\mathbf{b}_2$ является перпендикуляром, по которому $\mathbf{a}_2$ проецируется на $\mathbf{b}_1$ .

Рассмотрим формулу (3) — третий шаг алгоритма — в следующем варианте:

$\begin{array}{lcr} \mathbf{b}_3 = \mathbf{a}_3-(\mathbf{proj}_{\mathbf{b}_1}\mathbf{a}_3+\mathbf{proj}_{\mathbf{b}_2}\mathbf{a}_3) & & (6) \\ \end{array}$

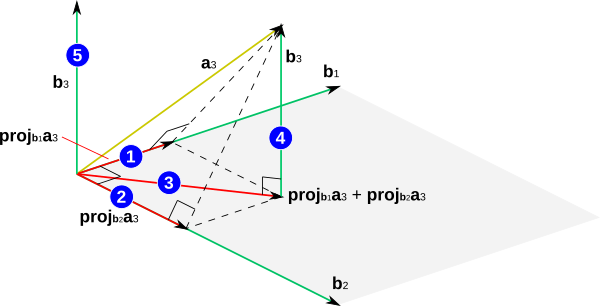
Её геометрическое представление изображено на рис. 2:

Рис. 2. Третий шаг процесса Грама — Шмидта

1 — получение проекции вектора $\mathbf{a}_3$ на $\mathbf{b}_1$ ;

2 — получение проекции вектора $\mathbf{a}_3$ на $\mathbf{b}_2$ ;

3 — вычисление суммы $\mathbf{proj}_{\mathbf{b}_1}\mathbf{a}_3 + \mathbf{proj}_{\mathbf{b}_2}\mathbf{a}_3$ , то есть проекции вектора $\mathbf{a}_3$ на плоскость, образуемую векторами $\mathbf{b}_1$ и $\mathbf{b}_2$ . Эта плоскость закрашена на рисунке серым цветом;

4 — вычисление $\mathbf{a}_3-(\mathbf{proj}_{\mathbf{b}_1}\mathbf{a}_3 + \mathbf{proj}_{\mathbf{b}_2}\mathbf{a}_3)$ , то есть перпендикуляра, которым выполняется проецирование конца $\mathbf{a}_3$ на плоскость, образуемую векторами $\mathbf{b}_1$ и $\mathbf{b}_2$ . Этот перпендикуляр — вычисляемый в формуле (6) вектор $\mathbf{b}_3$ ;

5 — перемещение полученного $\mathbf{b}_3$ в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (6).

На рисунке видно, что вектор $\mathbf{b}_3$ ортогонален векторам $\mathbf{b}_1$ и $\mathbf{b}_2$ , так как $\mathbf{b}_3$ является перпендикуляром, по которому $\mathbf{a}_3$ проецируется на плоскость, образуемую векторами $\mathbf{b}_1$ и $\mathbf{b}_2$ .

Таким образом, в процессе Грама — Шмидта для вычисления $\mathbf{b}_j$ выполняется проецирование $\mathbf{a}_j$ ортогонально на гиперплоскость?, формируемую векторами $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{j-1}$ . Вектор $\mathbf{b}_j$ затем вычисляется как разность между $\mathbf{a}_j$ и его проекцией. То есть $\mathbf{b}_j$ — это перпендикуляр? от конца $\mathbf{a}_j$ к гиперплоскости?, формируемой векторами $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{j-1}$ . Поэтому $\mathbf{b}_j$ ортогонален векторам, образующим эту гиперплоскость?.

1.2.1.4 Численная неустойчивость

При вычислении на ЭВМ по формулам (1) — (5) векторы $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_{N-1}$ часто не точно ортогональны из-за ошибок округления. Из-за потери ортогональности в процессе вычислений классический процесс Грама — Шмидта называют численно неустойчивым.

1.2.2 Модифицированный процесс Грама — Шмидта

Процесс Грама — Шмидта может быть сделан более вычислительно устойчивым путём небольшой модификации. Вместо вычисления $\mathbf{b}_j$ как: $\mathbf{b}_j = \mathbf{a}_j - \mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_j - \mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_j - \ldots - \mathbf{proj}_{\mathbf{b}_{j-1}}\,\mathbf{a}_j \; (7)$ этот вектор вычисляется следующим образом:

$\begin{array}{lclr} \mathbf{a}_j^{(1)} & = &\mathbf{a}_j - \mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_j & (8) \\ \mathbf{a}_j^{(2)} & = &\mathbf{a}_j^{(1)} - \mathbf{proj}_{\mathbf{b}_2} \, \mathbf{a}_j^{(1)} & (9) \\& \vdots & & \\ \mathbf{a}_j^{(j-2)} & = & \mathbf{a}_j^{(j-3)} - \mathbf{proj}_{\mathbf{b}_{j-2}} \, \mathbf{a}_j^{(j-3)} & (10) \\ \mathbf{b}_j & = & \mathbf{a}_j^{(j-2)} - \mathbf{proj}_{\mathbf{b}_{j-1}} \, \mathbf{a}_j^{(j-2)} & (11) \end{array}$

1.3 Вычислительное ядро алгоритма

Вычислительное ядро (computational kernel) алгоритма - это часть алгоритма, на которую приходится основное время его работы.

Вычислительное ядро последовательной версии метода ортогонализации Грамма-Шмидта можно составить из множественных (всего их $\frac{N(N-1)}{2}$ ) вычислений проекций : $\mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i}$

1.4 Макроструктура алгоритма

Данный алгоритм использует в качестве составных частей другие алгоритмы. В дальнейшем имеет смысл описывать алгоритм не в максимально детализированном виде (т.е. на уровне арифметических операций), а давать только его макроструктуру, то есть описывает структуру и состав макроопераций. Типичной макрооперацией, часто встречающиеся в алгоритме является оператор проекции векторов. Как записано и в описании ядра алгоритма, основную часть метода ортогонализации Грамма-Шмидта составляют множественные (всего их $\frac{N(N-1)}{2}$ ) вычисления оператора проекции.

1.5 Схема реализации последовательного алгоритма

Следующий алгоритм реализует нормализацию Грамма-Шмидта. Векторы $v_1,...,v_k$ заменяются набором ортонормированных векторов, которые имеют ту же линейную оболочку.

Вычислительная сложность этого $2Nk^2$ операции с плавающей точкой, где N - размерность векторов.

Последовательность исполнения метода следующая:

1. $\mathbf {b}_{1}=\mathbf {a}_{1}$

2. Далее для всех векторов $\mathbf {b}_{i}$ для $i=2 ... N$ производим вычисление по следующей формуле: ${\mathbf {b}}_{i}={\mathbf {a}}_{i}-\displaystyle \sum _{{j=1}}^{{i-1}}{\mathbf {proj}}_{{{\mathbf {b}}_{j}}}\,{\mathbf {a}}_{i}$ .

В ней на каждом шаге $i$ по очереди вычисляются все ${\mathbf {proj}}_{{{\mathbf {b}}_{j}}}\,{\mathbf {a}}_{i}$ для $j=1 ... i-1$

Пример реализации на Python. Функция работает для произвольного количества векторов любой размерности. При этом если количество векторов $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_N$ больше их размерности или они линейно зависимы то функция возвращает максимально возможное число линейно независимых векторов $\mathbf{b}_1,\;\ldots,\;\mathbf{b}_n$ , а остальные векторы $\mathbf{b}_{n+1},\;\ldots,\;\mathbf{b}_N$ нулевые.

import random

def GramSchmidt(*a):
    k=len(a[0])
    N=len(a);
    b = [[0] * k for i in range(N)]
    b[0]=a[0]
    for i in range(1,N):
        sum=a[i]
        for j in range(0,i):
            scolar_ab=0
            scolar_bb=0
            proj=[i for i in range(k)]
            for n in range(k):
                scolar_ab+=b[j][n]*a[i][n]
                scolar_bb+=b[j][n]*b[j][n]
            for n in range(k):
                proj[n]=(scolar_ab/scolar_bb)*b[j][n]
            for n in range(k):
                sum[n]-=proj[n]
        b[i]=sum
    return b;

l1=[random.randrange(0,10) for i in range(3)]
l2=[random.randrange(0,10) for i in range(3)]
l3=[random.randrange(0,10) for i in range(3)]
print(l1,l2,l3)
print(GramSchmidt(l1,l2,l3))

1.6 Последовательная сложность алгоритма

Для построения ортогонального набора векторов в последовательном варианте требуется:

При k=N:

$\frac{N(N-1)}{2}$ делений,

$\frac{N(N-1)(3N-1)}{2}$ сложений (вычитаний),

$\frac{3N^2 (N-1)}{2}$ умножений.

При k≠N

$\frac{N(N-1)}{2}$ делений,

$\frac{N(N-1)(3k-1)}{2}$ сложений (вычитаний),

$\frac{3Nk (N-1)}{2}$ умножений.

При классификации по последовательной сложности, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам с кубической сложностью.

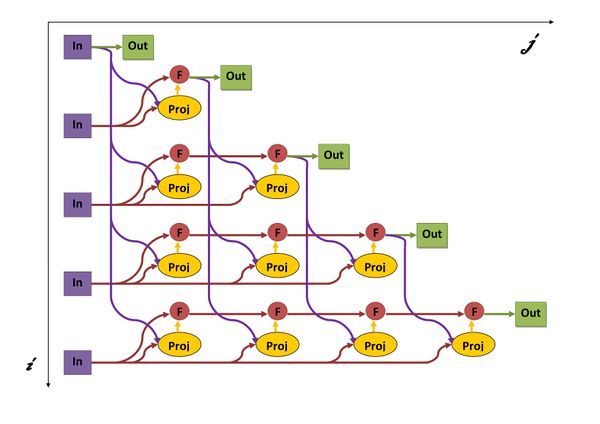
1.7 Информационный граф

Опишем граф алгоритма как аналитически, так и в виде рисунка.

Граф алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двух областей.

Первая группа вершин расположена в двумерной области, соответствующая ей операция $\mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i} = {\langle \mathbf{a_i}, \mathbf{b_j} \rangle \over \langle \mathbf{b_j}, \mathbf{b_j}\rangle} \mathbf{b_j} ,$ .

Естественно введённые координаты области таковы:

i — меняется в диапазоне от 2 до N, принимая все целочисленные значения;

j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения.

Аргументы операции следующие:

$a_i$ : элементы входных данных, а именно $a_i$ ;

$b_j$ : результат срабатывания операции, соответствующей вершине из второй группы, с координатой j.

Вторая группа вершин расположена в двухмерной области, соответствующая ей операция $a - b$ .

Естественно введённые координаты области таковы:

i — меняется в диапазоне от 2 до N, принимая все целочисленные значения;

j — меняется в диапазоне от 1 до i-1, принимая все целочисленные значения.

Аргументы операции следующие:

a:

j=1 - входные данные $a_j$

j>1 - результат срабатывания операции, соответствующей вершине из второй группы, с координатой j-1

b:

результат срабатывания операции, соответствующей вершине из первой группы, с координатой j

Рис. 5. Граф алгоритма с отображением входных и выходных данных. Proj - вычисление оператора проекции, F - операция a-b, In - входные данные, Out - результаты.

1.8 Ресурс параллелизма алгоритма

В параллельном варианте, в отличие от последовательного, вычисления $\mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i}$ можно выполнять параллельно. То есть после каждого вычисления $b_j$ можно запускать параллельное вычисление $\mathbf{proj}_{\mathbf{b_j}}\,\mathbf{a_i}$ для всех $i=j+1..N$

Для ортогонализации в параллельном варианте требуется последовательно выполнить следующие ярусы:

$N$ ярусов в каждом из которых будет выполнятся,
по $N - 1$ операторов проекций (в каждом из ярусов линейное количество проекций, в зависимости от яруса — от $N-1$ до $1$ ),
по $N - 1$ сложений (в каждом из ярусов линейное количество сложений, в зависимости от яруса — от $N-1$ до $1$ ),

При классификации по высоте (количество ярусов в ЯПФ ) ЯПФ, таким образом, ортогонализация Грамма-Шмидта относится к алгоритмам со сложностью $O(N)$ .

При классификации по ширине (максимальное количество вершин в ярусе) ЯПФ его сложность будет $O(N^2)$ .

1.9 Входные и выходные данные алгоритма

Входные данные: множества линейно независимых векторов $\mathbf {a} _{1},\;\ldots ,\;\mathbf {a} _{N}$ , каждый из которых описывается $\mathbf{ a_i= [a^i_1, a^i_2, ..., a^i_k]}$ .

Дополнительные ограничения:

вектора $\mathbf {a} _{1},\;\ldots ,\;\mathbf {a} _{N}$ линейно независимы, поэтому $k \geqslant N$ .

Объём входных данных: $Nk$

Выходные данные: множество ортогональных векторов $\mathbf {b} _{1},\;\ldots ,\;\mathbf {b} _{N}$ , каждый из которых описывается $\mathbf{ b_i= [b^i_1, b^i_2, ..., b^i_k]}$ .

Объём выходных данных: $Nk$

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение кубической к квадратичной).

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, также линейна.

Алгоритм почти полностью детерминирован — единственность результата выполнения гарантирована, однако возможно накопление ошибок округления при использовании классического процесса Грама-Шмидта. При этом модифицированный алгоритм дает более хороший результат.

Алгоритм является численно неустойчивым — ошибки округления могут привести к неортогональности полученных векторов.

Процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов.

Кроме того, процесс Грама — Шмидта может применяться к линейно зависимым векторам. В этом случае он выдаёт $\mathbf{0}$ (нулевой вектор) на шаге $j$ , если $\mathbf{a}_j$ является линейной комбинацией векторов $\mathbf{a}_1,\;\ldots,\;\mathbf{a}_{j-1}$ . Если это может случиться, то для сохранения ортогональности выходных векторов и для предотвращения деления на ноль при ортонормировании алгоритм должен делать проверку на нулевые векторы и отбрасывать их. Количество векторов, выдаваемых алгоритмом, будет равно размерности подпространства, порождённого векторами (т.е. количеству линейно независимых векторов, которые можно выделить среди исходных векторов).

Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами ― QR-разложение, что есть частный случай разложения Ивасавы.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Примеры библиотек, содержащих реализации алгоритма ортогонализации Грама-Шмидта:

2.7.1 Реализация для пакета Mathematica

Данный скрипт, предназначенный для пакета Mathematica, проводит процесс ортогонализации Грама ― Шмидта над векторами, заданными в фигурных скобках последней строки. Количество векторов и их координат могут быть произвольными. В данном случае для примера взяты векторы {-2,1,0}, {-2,0,1}, {-0.5,-1,1}.

Projection[v1_, v2_] := (v1.v2*v2)/v2.v2
MultipleProjection[v1_, vecs_] := Plus @@ (Projection[v1, #1] &) /@ vecs
GramSchmidt[mat_] := Fold[Join[#1, {#2 - MultipleProjection[#2, #1]}] &, {}, mat]
GramSchmidt[{{-2, 1, 0}, {-2, 0, 1}, {-0.5, -1, 1}}]

2.7.2 Реализация для Maxima

Данный скрипт, предназначенный для пакета Maxima, проводит процесс ортогонализации Грама ― Шмидта над векторами, заданными в квадратных скобках. Количество векторов и их координат могут быть произвольными.

В данном случае для примера взяты векторы [-2,1,0], [-2,0,1], [-0.5,-1,1].

load(eigen);
x: matrix ([-2,1,0],[-2,0,1],[-0.5,-1,1]);
y: gramschmidt(x);

2.7.3 Реализация для MATLAB

В MATLAB существует встроенная функция [Q,R]=qr(A) которая осуществляет ортогонализацияю Грамма-Шмидта столбцов матрицы А. При этом столбцы матрицы предполагаются линейнонезависимыми.

[Q, R] = qr(A) возвращает матрицы Q с ортонормированными столбцами и обратимую верхнетреугольную матрицу R, так что A=Q*R

3 Литература

Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. — М.: Наука.
Гельфанд И. М. Лекции по линейной алгебре. — 5-е. — М.: Добросвет, МЦНМО, 1998. — 319 с. — ISBN 5-7913-0015-8.
Ильин В. А., Позняк Э. Г. Линейная алгебра. 6-е изд. — М.: Физматлит, 2010. — 280 с. — ISBN 978-5-9221-0481-4.
Халмош П. Конечномерные векторные пространства = Finite-Dimensional Vector Spaces. — М.: Физматгиз, 1963. — 263 с.
Фаддеев Д. К. Лекции по алгебре. — 5-е. — СПб.: Лань, 2007. — 416 с.

4 Ссылки

https://ru.wikipedia.org/wiki/Процесс_Грама_―_Шмидта Процесс Грама ― Шмидта