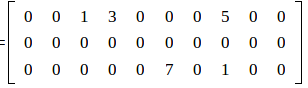Участник:Lexaloris/Умножение разреженной матрицы на вектор

Умножение разреженной матрицы на вектор
Последовательный алгоритм
Последовательная сложность	$O(k)$
Объём входных данных	$k + m$
Объём выходных данных	$n$
Параллельный алгоритм
Высота ярусно-параллельной формы	$O(m)$
Ширина ярусно-параллельной формы	$O(n)$

Авторы страницы: A.Д. Новоселов и П.А. Кочетков

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

1.1.1 Хранение ненулевых элементов разреженной матрицы

1.1.1.1 Разреженный строчной формат

Одной из наиболее ши­роко используемых схем хранения разреженных матриц является разреженный строчный формат. Эта схема предъявляет минимальные требования к памяти и в то же время оказывается очень удобной для умножения разреженной матрицы на вектор. Например, рассмотрим формат хранения разряженной матрицы $A$:

Значения нену­левых элементов матрицы и соответствующие столбцовые индексы хранятся в этой схеме по строкам в двух массивах $AN$ и $JA$ соответственно. Используется также массив указателей $IA$, отмечающих позиции массивов $AN$ и $JA$, с которых начинается описание очередной строки. Дополнительная компо­нента в $IA$ содержит указатель первой свободной позиции в $JA$ и $AN$.

Таким образом $A$ представляется в виде:

  IA = [ 1 4 4 6 ]
  JA = [ 3 4 8 6 8 ]
  AN = [ 1 3 5 7 1 ]

Данный способ представления называют полным, поскольку представлена вся матрица $A$, и упорядоченным, поскольку эле­менты каждой строки хранятся в соответствии с возрастанием столбцовых индексов. Таким образом, это строчное представление, полное и упорядоченное, или сокращенно (RR (С) О).

1.1.1.2 Неупорядоченное представление

Представления разреженных матриц необязательно должны быть упорядочены в том смысле, что, хотя упорядоченность строк поддерживается, внутри каждой строки элементы могут храниться в произвольном порядке. Для матрицы А нашего примера вполне можно было бы использовать и строчное представление, полное, но неупорядоченное (RR (С) U ).

Неупорядоченное представление $A$:

  IA = [ 1 4 4 6 ]
  JA = [ 8 3 4 8 6 ]
  AN = [ 5 1 3 1 7 ]

Неупорядоченные представления могут быть очень удобны. Результаты большинства матричных операций получаются не­ упорядоченными, и упорядочение их стоило бы больших затрат машинного времени. В то же время, за немногими исключениями, алгоритмы для разреженных матриц не требуют, чтобы представления были упорядоченными.

1.1.2 Умножение разреженной матрицы на вектор

Пусть $N$ — число строк матрицы. Для каждой ее строки $I$ матрицы мы находим с помощью $IA$ значения первой $IAA$ и последней $IAB$ позиций, занимаемых элементами строки $I$ в массивах $JA$ и $AN$. Затем, чтобы вычислить скалярное произведение строки $I$ и вектора $B$, мы просто просматриваем $JA$ и $AN$ на отрезке от $IAA$ до $IAB$: каждое значение, хранимое в $JA$, есть столбцовый индекс и используется для извлечения из массива $B$ элемента, который должен быть умножен на соответствующее число из $AN$. Результат каж­дого умножения прибавляется к $C(I)$.

1.2 Математическое описание алгоритма

Исходные данные:

$IA, JA, AN$ - заданная матрица в форме (RR (С) U);

$B$ - заданный заполненный вектор;

$N$ - число строк матрицы.

Выход: $C$ вектор-произведение размерности $N$.

Формулы метода:

$\begin{align} & IAA_{i} = IA(i), \quad i \in [1, N], \\ & IAB_{i} = IA(i + 1) - 1, \quad i \in [1, N], \\ & c_{i} = \sum\limits_{j = IAA_{i}}^{IAB_{i}} AN(j)B(JA(j)), \quad i \in [1, N] \\ \end{align}$

1.3 Вычислительное ядро алгоритма

Вычислительным ядром, т.е. той частью алгоритма, на которую приходится основное время его работы, является вычисление значения $i$-го элемента $c_{i}$ вектора-произведения, т.е произведения строки $I$ матрицы $A$ и вектора $B$ по формуле:

$\begin{align} & c_{i} = \sum\limits_{j = IAA_{i}}^{IAB_{i}} AN(j)B(JA(j)), \quad i \in [1, N] \\ \end{align}$

1.4 Макроструктура алгоритма

Основу алгоритма составляет вычисление значения $i$-го элемента $c_{i}$ вектора-произведения:

$\begin{align} & c_{i} = \sum\limits_{j = IAA_{i}}^{IAB_{i}} AN(j)B(JA(j)), \quad i \in [1, N] \\ \end{align}$

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая:

Далее для всех $i$ от $1$ до $N$ по нарастанию выполняются:

1. $c_{i} = 0; IAA = IA(i); IAB = IA(i + 1 ) - 1$

После этого, если $(IAB \le IAA)$:

2. Для всех $j$ от $IAA$ до $IAB$ выполняется:

$c_{i} = \sum\limits_{j = IAA_{i}}^{IAB_{i}} AN(j)B(JA(j))$

Псевдокод алгоритма:

   FOR I = 1, N                          (1)
      U = 0.                             (2) 
      IAA = IA(I)                        (3) 
      IAB = IA(I + 1 ) - 1               (4)
      IF NOT(IAB.LT.IAA)                 (5)
          FOR J = IAA, IAB               (6)
          C(I) = U + AN(J)*B(JA(J))      (7)

1.6 Последовательная сложность алгоритма

Для всего алгоритма потребуется выполнить $O(k)$ операций, как в строке стр.7 псевдокода алгоритма (п.1.5), где $k$ - число ненулевых эле­ментов матрицы.

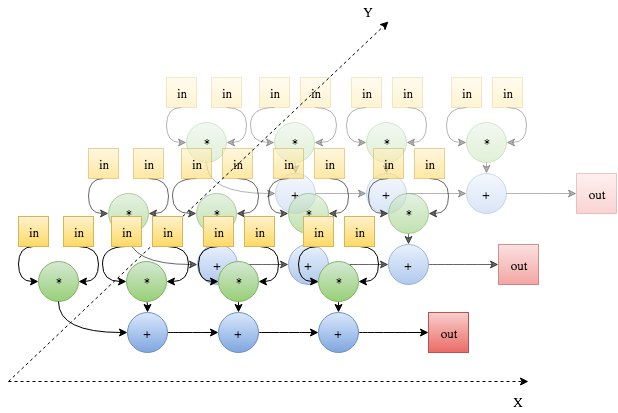
1.7 Информационный граф

На рисунке 1 изображен информационный граф алгоритма.

Рисунок 1. Информационный граф алгоритма.

По оси $X$ для отдельной строки $I$ матрицы отложены в пределах первой $IAA$ и последней $IAB$ позиций ненулевых элементов значения $AN$ и соответствуюие им по столбцовомым индексам, хранимимым в $JA$, значения $B$ элементов. Пары этих значений обозначены желтыми квадратиками $(in)$. Значения in попарно скалярно перемножаются (зеленый кружочек) и суммируются (синий кружочек) в результат значения элемента вектора-произведения $c_{i}$, т.е $out$(красный квадратик) с строковым индексом, соответствующем номеру строки матрицы.

По оси $Y$ отложена схема вычисление значения каждого элемента вектора-произведения для каждой строки матрицы.

1.8 Ресурс параллелизма алгоритма

Алгоритм обладает возможностью выполняться параллельно, что позволяет значительно ускорить вычисления. Вычисление значения каждого элемента вектора-произведения для каждой строки матрицы и элемента вектора $B$ можно проводить на отдельных процессорах. Максимальная эффективность вычислений достигается при наличии не менее, чем $N$ процессоров, т.е отдельный процессор на вычисление значения каждого элемента вектора-произведения. На процессоре выполняется $k(i)$ последовательных операций умножения и сложения. Поэтому число ярусов для $i$-ого процессора равно $k(i)$.

Для параллельного выполнения алгоритма требуется:

• $N$ ярусов умножений и сложений,
• в каждом из ярусов $k \lt \lt m$ операций.

При классификации по высоте ЯПФ, алгоритм имеет линейную сложность. При классификации по высоте ЯПФ также линейную.

1.9 Входные и выходные данные алгоритма

Входные данные:

• $IA, JA, AN$ - заданная матрица в форме (RR (С) U) c $k$ ненулевыми элементами и $N$ строками, $m$ столбцами;

• $B$ - заданный заполненный вектор c $m$ элементами;

Объем входных данных: $k + m$

Выходные данные: $C$ вектор-произведение размерности $N$.

Объем выходных данных: $N$

1.10 Свойства алгоритма

Алгоритм в рамках выбранной версии полностью детерминирован.

Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – константа.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Алгоритм релизован в составе библиотек:

• SparseLib++[1]
• cuSPARSE [2]
• uBLAS [3]
• Intel MKL [4]

3 Литература

• [1] С. Писсанецки. Технология разреженных матриц. Изд. Мир, 1988.
• [2] В. В. Воеводин, Вл.В. Воеводин. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002.