Участник:Юлия Жосан/Разбиение вершин графа на равные по мощности блоки методом рекурсивной координатной бисекции

Автор: Юлия Жосан

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

---

Декомпозиция графа - это задача его разбиения на непересекающиеся подмножества доменов, для их последующей параллельной обработки группой процессоров. Основная сложность использования параллельных методов состоит в поиске оптимальной декомпозиции, которая дает сбалансированное распределение доменов по процессорам. Выделяют два основных свойства оптимальной декомпозиции, которые должны выполняться одновременно:

• минимизация максимального веса исходящих из домена ребер
• равномерное распределение по доменам суммарного веса узлов/ребер

Покоординатная декомпозиция основана на рекурсивном делении пополам сети по координатной оси, вдоль которой область наиболее протяженная, соотношение размеров полученных частей зависит от требуемого количества доменов в каждой из них. Этот метод применяется для обработки сеток больших размеров (объем описания сетки превышает объем оперативной памяти одного процессорного узла).

Основные этапы работы алгоритма:

1. Выбор направления, вдоль которого будут упорядочиваться вершины домена
2. Упорядочивание вершин вдоль выбранного в п.1 направления
3. Вычисление номера m первой вершины второго домена
4. Формирование двух новых доменов, первый из которых включает вершины от первой до m-1 входящего домена, а второй включает вершины с m до последней вершины входящего домена
5. Запуск алгоритма для полученных в п.4 доменов

Выделяют следующие достоинства данного алгоритма:

• высокая скорость работы
• низкий уровень дисбаланса распределения вершин между доменами
• экономичность по памяти

1.2 Математическое описание алгоритма

---

Пусть на вход алгоритму подаются следующие данные:

• неориентированный граф $G=(V, E)$, где $V$ - множество вершин, $E$ - множество ребер
• Требуемое число доменов $p$

На выходе алгоритма требуется получить множество доменов $\{S_{p}\}$.Это множество $p$ непересекающихся подмножеств $\{V_{i}\}$:
$V=\bigcup\limits_{i=1}^{p} V_{i}$, $V_{i}\cap V_{j}=\emptyset$ для $i\not=j$ при котором минимизируются следующие функционалы:

• суммарный вес вершин в домене: $\vert S_{p}\vert=\sum\limits_{i=1}^{p} \vert v_{i} \vert\rightarrow min$
• суммарный вес разрезанных ребер:$\sum\limits_{ij} \vert e_{ij} \vert\rightarrow min , v_{i}\in S_{l}, v_{j}\in S_{r}, S_{l}\cap S_{r}=\emptyset$

Опишем подробнее схему работу рекурсивного алгоритма:

1. Выбор оси, вдоль которой будет осуществляться сортировка. Для этого вычисляется величина $l_{k}=max\left( v_{i}^{k}\right)-min\left(v_{i}^{k}\right) , v_{i}^{k}\in V , k$ - координатная ось, и выбирается ее максимальное значение.
2. Сортировка множества вершин $V$ по выбранной в п.1 координате по возрастанию номеров коодинат вершин
3. Вычисляется номер вершины, по которой пойдет разбиение множества: $m=(iend-istart+1)*\frac{\frac{p+1}{2}}{p}$, где $iend, istart$ - номер первой вершины в множестве и номер последней вершины в множестве соответственно
4. Множество вершин делится на две части: $V_{l}=|v_{l}|, l=istart..m ,V_{r}=|v_{r}|, r=m+1..iend$
5. Алгоритм запускается для $V_{l}$ и $V_{r}$
6. Алгоритм останавливается на итерации, для которой $|V_{l}|=1 , |V_{r}|=1$

1.3 Вычислительное ядро алгоритма

---

Вычислительное ядро алгоритма составляют:

• сортировка массива координат вершин $V$ (могут применяться различные виды сортировок)
• вычисление величины $l_{k}$ - координатной оси
• вычисление величины $m$ - точки раздела множества

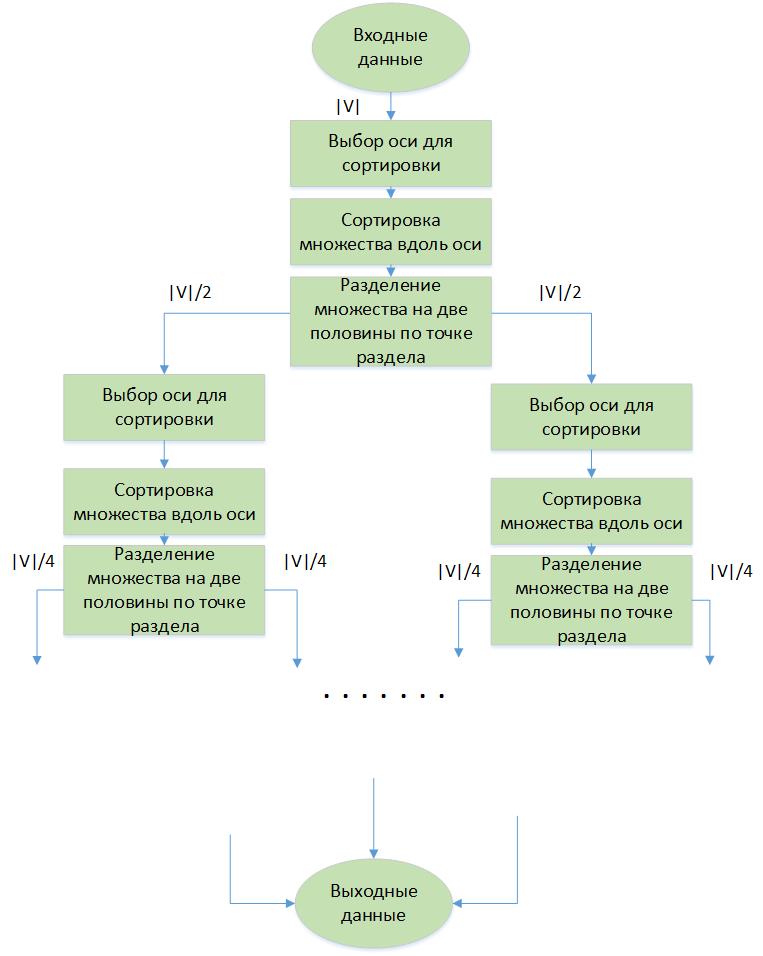
1.4 Макроструктура алгоритма

---

Основной составляющей метода является повторяющиеся сортировки множества координат вершин $V$ на каждом рекурсивном шаге. Всего таких шагов $p-1$.

1.5 Схема реализации последовательного алгоритма

---

Представим последовательную реализацию метода рекурсивной координатной бисекции с помощью псевдокода:
$BisectCoordRec\{V, iend, istart , p\}$
{
Шаг 1: $l_{k}=argmax{max\left( v_{i}^{k}\right)-min\left(v_{i}^{k}\right)}$ - //определение оси для сортировки
Шаг 2: $Sort(V, iend, istart ,l_{k})$- //сортировка вершин по выбранной координате
Шаг 3: $m=(iend-istart+1)*\frac{\frac{p+1}{2}}{p}$ - //поиск точки для разделения множества вершин
Шаг 4: $Bisect\left(V,(iend-istart) , V_{l}, \frac{p+1}{2}, V_{r}, \frac{\frac{(iend-istart)*(p+1)}{2}}{p}\right)$- //разделение массива вершин на два
Шаг 5: $if |V_{l}|\gt 1 : BisectCoordRec\{V_{l},\frac{(iend-istart)*\frac{p+1}{2}}{p} , \frac{p+1}{2}, p\}$
Шаг 6: $if |V_{r}|\gt 1 : BisectCoordRec\{V_{r}, (iend-istart) - \frac{(iend-istart)*\frac{p+1}{2}}{p} , p - \frac{p+1}{2}, p\}$
}

1.6 Последовательная сложность алгоритма

---

Пусть в графе $G$ содержится $|V|=n$ вершин.

• Для определения координат $iend, istart$ требуется $O(n)$ попарных сравнений
• Для сортировки массива вершин по координате требуется $O(nlog_{2}n)$ попарных сравнений

Так как всего осуществляется $p-1$ шагов рекурсии, глубина ее составляет $-log_{2}p+1$ Значит можно определить сложность алгоритма следующим образом: $O(nlog_{2}nlog_{2}p)$

1.7 Информационный граф

---

1.8 Ресурс параллелизма алгоритма

---

Структура параллельного алгоритма:

1. Подготовительный этап:
   • определение числа и объема требуемых доменов по процессорам
     • Пусть имеется граф с n вершинами, он распределяется по k доменам. Тогда глубина рекурсии - $log_{2}k$, что равняется числу ярусов.
2. Разделение доменов по процессорам:
   • вызов рекурсивной покоординатной бисекции по процессорам:
     • сортировка вершин графа (на i-м ярусе выполняется $2^i$ операций)
     • разделение на два подграфа для разделения по доменам
3. Параллельные вызовы алгоритма для каждого процессора
   • вызов локальной координатной бисекции по доменам

Пусть сложность сортировки равна $O(n\log_2{n})$.
Тогда сложность алгоритма можно представить в следующем виде: $O(\sum\limits_{i=0}^{log_2{k}}\frac{n}{2^i}\log_2{\frac{n}{2^i}})= O(\sum\limits_{i=0}^{log_2{k}}(n\frac{(log_2{n}-i)}{2^i}))= O(n(\sum\limits_{i=0}^{log_2{k}}(\frac{log_2{n}}{2^i})-\sum\limits_{i=0}^{log_2{k}}(\frac{i}{2^i})))= O(n\log_2{n})-O(n)=O(n\log_2{n})$.

1.9 Входные и выходные данные алгоритма

---

Вход алгоритма:

• неориентированный граф $G=(V, E)$, где $V$ - множество вершин, $E$ - множество ребер
• Требуемое число доменов $p$

Выход алгоритма:

• $p$ доменов $\{S_{p}\}$, задающих декомпозицию графа

1.10 Свойства алгоритма

---

• Низкий уровень дисбаланса распределения вершин между доменами. Т.е. количество вершин в доменах примерно одинаковое.
• Алгоритм детерминирован в случае использования устойчивой сортировки вершин.
• Алгоритм достаточно прост в реализации.

2 Программная реализация алгоритма

---

2.7 Существующие реализации алгоритма

---

Параллельные реализации:

• ParMETIS
• JOSTLE
• PT-SCOTCH
• ZOLTAN

Последовательные реализации:

• METIS
• JOSTLE
• SCOTCH
• CHACO
• PARTY

3 Литература

---

[1] Якобовский М.В. Введение в параллельные методы решения задач: Учебное пособие / Предисл.: В. А. Садовничий. – М.: Издательство Московского университета, 2012. – 328 с., илл. – (Серия «Суперкомпьютерное образование»), ISBN 978-5-211-06382-2 URL: http://lira.imamod.ru/ITTPMOPS/
[2] Головченко Е.Н. Декомпозиция расчетных сеток для решения задач механики сплошных сред на высокопроиводительных вычислительных системах. Дисс ... канд. ф.-м.наук. Институт прикладной математики им. М. В. Келдыша РАН, г. Москва URL: http://keldysh.ru/council/3/D00202403/golovchenko_diss.pdf