Участник:Sergey Lavrushkin/EM-алгоритм кластеризации

Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 12.11.2016 Авторы этой статьи считают, что задание выполнено.

Эта работа прошла предварительную проверку Дата последней правки страницы: 12.11.2016 Данная работа соответствует формальным критериям. Проверено Algoman.

EM-алгоритм кластеризации (1 итерация)
Последовательный алгоритм
Последовательная сложность	$O(nkq^2)$
Объём входных данных	$nq + 1$
Объём выходных данных	$k(n + q^2 + q + 1)$
Параллельный алгоритм
Высота ярусно-параллельной формы	$O(\log{nk})$
Ширина ярусно-параллельной формы	$O(nk)$

Автор статьи: Сергей Лаврушкин (группа 620)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

1.1.1 EM-алгоритм

EM-алгоритм (англ. expectation-maximization) — алгоритм, используемый в математической статистике для нахождения оценок максимального правдоподобия параметров вероятностных моделей, в случае, когда модель зависит от некоторых скрытых переменных. Каждая итерация алгоритма состоит из двух шагов. На E-шаге (expectation) вычисляется ожидаемое значение функции правдоподобия, при этом скрытые переменные рассматриваются как наблюдаемые. На M-шаге (maximization) вычисляется оценка максимального правдоподобия, таким образом увеличивается ожидаемое правдоподобие, вычисляемое на E-шаге. Затем это значение используется для E-шага на следующей итерации. Алгоритм выполняется до сходимости.

Как правило, ЕМ-алгоритм применяется для решения задач двух типов:

• К первому типу можно отнести задачи, связанные с анализом действительно неполных данных, когда некоторые статистические данные отсутствуют в силу каких-либо причин.
• Ко второму типу задач можно отнести те задачи, в которых функция правдоподобия имеет вид, не допускающий удобных аналитических методов исследования, но допускающий серьезные упрощения, если в задачу ввести дополнительные «ненаблюдаемые» (скрытые, латентные) переменные. Примерами прикладных задач второго типа являются задачи распознавания образов, реконструкции изображений. Математическую суть данных задач составляют задачи кластерного анализа, классификации и разделения смесей вероятностных распределений.

Алгоритм основан на методике итеративного вычисления оценок максимального правдоподобия, предложенной в 1977 г. (A. P. Demster, N. M. Laird, D. B. Rubin. Maximum Likelihood from Incomplete Data via the EM Algorithm).

1.1.2 Кластеризация с помощью EM-алгоритма

Кластеризация — задача разбиения заданной выборки объектов (ситуаций) на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались . В основе идеи применения EM-алгоритма для кластеризации лежит предположение, что исследуемое множество данных может быть смоделировано с помощью линейной комбинации многомерных нормальных распределений, а целью является оценка параметров распределения, которые максимизируют логарифмическую функцию правдоподобия, используемую в качестве меры качества модели. К оцениваемым параметрам относятся математические ожидания и ковариационные матрицы. Предполагается, что любое наблюдение принадлежит ко всем кластерам, но с разной вероятностью. Задача заключается в "подгонке" распределений смеси к данным, а затем в определении вероятностей принадлежности наблюдения к каждому кластеру. Наблюдение должно быть отнесено к тому кластеру, для которого данная вероятность выше.

Алгоритм EM основан на вычислении расстояний. Он может рассматриваться как обобщение кластеризации на основе анализа смеси вероятностных распределений. В процессе работы алгоритма происходит итеративное улучшение решения, а остановка осуществляется в момент, когда достигается требуемый уровень точности модели. Мерой в данном случае является монотонно увеличивающаяся статистическая величина, называемая логарифмическим правдоподобием.

1.2 Математическое описание алгоритма

Исходные данные:

• $k$ — число кластеров,
• $X =\{x_{1}, x_{2}, ..., x_{n}\}$ — множество из $n$ наблюдений размерности $q$: $x_{i} = (x_{i1}, ..., x_{iq})$.

Вычисляемые данные:

• $(w, \theta) = (w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)$ — параметры смеси гауссовых распределений,
• $Y$ — матрица размера $n \times k$ с вероятностями членства в кластерах.

1.2.1 Постановка задачи разделения смеси гауссовых распределений

Пусть $w_1, ..., w_k$ — априорные вероятности кластеров, $p_1(x), ..., p_k(x)$ — плотности распределения кластеров. Тогда плотность распределения вектора признаков $x$ сразу по всем кластерам равна:

$\begin{align} p(x) = \sum_{j=1}^{k}w_jp_j(x) \end{align}$

Необходимо на основе выборки оценить параметры модели $w_1, ..., w_k, p_1(x), ..., p_k(x)$. Это позволит оценивать вероятность принадлежности к кластеру и, таким образом, решить задачу кластеризации. Такая задача называется задачей разделения смеси распределений:

$\begin{align} p(x) = \sum_{j=1}^{k}w_jp_j(x),\quad p_j(x) = \phi(\theta_j; x), \end{align}$

где $\theta_j$ — параметры распределения $p_j(x)$. В случае смеси гауссовых распределений в $q$-мерном пространстве признаков $\phi(\theta_j; x)$ имеют следующий вид:

$\begin{align} \phi(\theta_j; x) = \frac{1}{\Big(2\pi\Big)^{\frac{q}{2}}\sqrt{|\Sigma_j|}}\exp{\bigg\{-\frac{\delta^2}{2}\bigg\} }, \end{align}$

где:

• $\Sigma_j$ — ковариационная матрица размером $q \times q$,
• $\mu_j$ — $q$-мерный вектор математических ожиданий,
• $\delta^2 = \Big( x - \mu_j \Big)^T \Sigma_j^{-1} \Big( x - \mu_j \Big)$ — квадратичное расстояние Махаланобиса.

В случае смеси гауссовых распределений получаем, что $\theta_j = (\mu_j, \Sigma_j)$. То есть для решения задачи разделения смеси гауссовых распределений необходимо оценить вектор параметров $(w, \theta) = (w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)$. Согласно принципу максимизации правдоподобия:

$\begin{align} w, \theta = \underset{w, \theta}{\operatorname{argmax}} \sum_{i=1}^{n}\ln{p(x_i)} = \underset{w, \theta}{\operatorname{argmax}} \sum_{i=1}^{n}\ln{\sum_{j=1}^{k}w_jp_j(x_i)} \end{align}$

Таким образом, имеет место задача максимизации суммы логарифмов сумм, решение которой представляет большую трудность. В таком случае полезным оказывается итеративный метод решения — EM-алгоритм.

1.2.2 EM-алгоритм

Оптимальные параметры задачи разделения смеси гауссовых распределений отыскиваются последовательно с помощью итерационного EM-алгоритма. Основная идея – вводится вспомогательный вектор скрытых переменных. Это позволяет свести сложную оптимизационную задачу к последовательности итераций по пересчету коэффициентов (скрытых переменных по текущему приближению вектора параметров - E-шаг) и максимизации правдоподобия (с целью найти следующее приближение вектора - М-шаг).

EM-алгоритм заключается в следующем:

1. В начале работы алгоритма задаются параметры начального приближения. Наиболее общим способом инициализации является присвоение элементам матрицы математических ожиданий случайных значений $\mu_j \leftarrow Random$, начальные ковариационные матрицы определяются как единичные $\Sigma_j \leftarrow I$, веса кластеров задаются одинаковыми $w_i \leftarrow \frac{1}{k}$. Также в качестве начальных параметров можно использовать результат работы алгоритма K-means. (Данная эвристика применяется, так как K-means требуется намного меньше итераций до достижения стабилизации, в то время как каждый шаг EM требует больших вычислительных затрат).
2. Далее итеративно выполняется следующая пара процедур:
   • E-шаг: используя текущее значение вектора параметров $(w, \theta) = (w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)$, вычисляются значения скрытых переменных $y_{ij}$:

     $\begin{align} & y_{ij} = \frac{w_j p_j(x_i)}{\sum_{l=1}^{k}w_lp_l(x_i)} \end{align}$

   • М-шаг: переоценка вектора параметров, используя текущие значения скрытых переменных:

     $\begin{align} & n_j = \sum_{i = 1}^{n}y_{ij}, \\ & \mu_j^{new} = \frac{1}{n_j} \sum_{i = 1}^{n}y_{ij}x_i, \\ & \Sigma_j^{new} = \frac{1}{n_j} \sum_{i = 1}^{n}y_{ij}(x_i - \mu_j^{new})(x_i - \mu_j^{new})^T,\\ & w_j^{new} = \frac{n_j}{n}. \end{align}$

Итерации происходят до сходимости (норма разности векторов скрытых переменных или изменение логарифмического правдоподобия на каждой итерации не будет превышать заданную константу) или достижения максимального числа итераций.

1.3 Вычислительное ядро алгоритма

В вычислительное ядро EM-алгоритма входят:

• Вычисление скрытых переменных $y_{ij}$ на E-шаге (всего их $nk$).
• Переоценка вектора параметров $(w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)$ на M-шаге, используя текущие значения скрытых переменных $y_{ij}$.

1.4 Макроструктура алгоритма

Как записано в описании ядра алгоритма, основную часть метода составляют множественные вычисления скрытых переменных $y_{ij}$ на E-шаге и обновление вектора параметров $(w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)$ на M-шаге. Также стоит выделить вычисление определителя и обратной матрицы ковариационных матриц $\Sigma_j$ в начале E-шага.

1.5 Схема реализации последовательного алгоритма

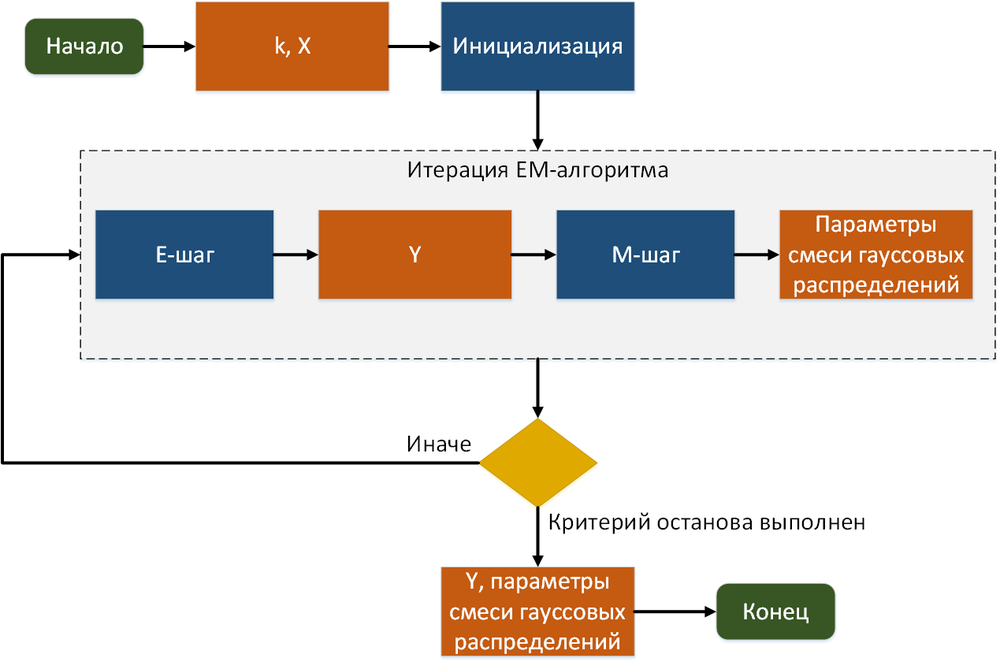
Последовательная реализация алгоритма EM может быть проиллюстрирована с помощью следующего псевдокода:

1. Инициализация: установка начальных значений $\mu, \, \Sigma_j \, (j = \overline{1, k}), \, w$.
2. Пока изменение логарифмического правдоподобия $\Delta llh \geq \epsilon$ и не достигнуто максимальное число итераций $m$, выполнять шаги E и M.

Шаг E

def E-step:
    Инициализировать нулевыми значениями [math]\mu^{'}, \, \Sigma_j^{'} \, (j = \overline{1, k}), \, w^{'}, \, llh[/math]
    for [math]j = \overline{1, k}[/math]:
        Вычислить определитель и обратную матрицу матрицы [math]\Sigma_j[/math]
    for [math]i = \overline{1, n}[/math]:
        [math]sump_i = 0[/math]
        for [math]j = \overline{1, k}[/math]:
            [math]\delta_{ij}^2 = \big( x_i - \mu_j \big)^T \Sigma_j^{-1} \big( x_i - \mu_j \big)[/math]
            [math]g_{ij} = \frac{w_j}{{(2 \pi)}^\frac{q}{2}\sqrt{|\Sigma_j|}}\exp{\big\{-\frac{\delta_{ij}^2}{2}\big\} }[/math]
            [math]sump_i \mathrel{+}= g_{ij}[/math]
        [math]y_i = \frac{g_i}{sump_i}[/math]
        [math]llh \mathrel{+}= \ln(sump_i)[/math]
        [math]\mu^{'} \mathrel{+}= x_iy_i^T[/math]
        [math]w^{'} \mathrel{+}= y_i[/math]

Шаг M

def M-step:
    for [math]j = \overline{1, k}[/math]:
        [math]\mu_j = \frac{\mu_j^{'}}{w_j^{'}}[/math]
        for [math]i = \overline{1, n}[/math]:
            [math]\Sigma_j^{'} \mathrel{+}= (x_i - \mu_j)y_{ij}(x_i - \mu_j)^T[/math]
        [math]\Sigma_j = \frac{\Sigma_j^{'}}{w_j^{'}}[/math]
    [math]w = \frac{w^{'}}{n}[/math]

Логаририфмическое правдоподобие вычисляется как:

$\begin{align} llh=\sum_{i=1}^{n}\ln{(sump_i)} \end{align}$

Матрицы $\mu^{'}, \, \Sigma_j^{'} \, (j = \overline{1, k}), \, w^{'}$ являются временными и используются только для вычислений.

1.6 Последовательная сложность алгоритма

Последовательная сложность одной итерации EM-алгоритма:

1. E-шаг:
   В случае недиагональных ковариационных матриц сложность вычислений:
   • Определителей ковариационных матриц $|\Sigma_j|$ ($j = \overline{1, k}$) методом Гаусса: $O(kq^3)$,
   • Матриц, обратных ковариационным матрицам $\Sigma_j^{-1}$ ($j = \overline{1, k}$) методом Гаусса-Жордана: $O(kq^3)$,
   • Скрытых переменных $y_{ij}$ ($i = \overline{1, n}, j = \overline{1, k}$): $O(nkq^2)$.
   В случае диагональных ковариационных матриц сложность вычислений:
   • Определителей ковариационных матриц $|\Sigma_j|$ ($j = \overline{1, k}$): $O(kq)$,
   • Матриц, обратных ковариационным матрицам $\Sigma_j^{-1}$ ($j = \overline{1, k}$): $O(kq)$,
   • Скрытых переменных $y_{ij}$ ($i = \overline{1, n}, j = \overline{1, k}$): $O(nkq)$.
   Получаем, что последовательная сложность E-шага в случае недиагональных ковариационных матриц имеет порядок $O(kq^3 + nkq^2)$, а в случае диагональных ковариационных матриц — $O(nkq)$.
2. М-шаг:
   В случае недиагональных ковариационных матриц сложность вычислений:
   • Обновление математических ожиданий $\mu_j$ ($j = \overline{1, k}$): $O(nkq)$,
   • Обновление ковариационных матриц $\Sigma_j$ ($j = \overline{1, k}$): $O(nkq^2)$,
   • Обновление весов кластеров $w_j$ ($j = \overline{1, k}$): $O(nk)$.
   В случае диагональных ковариационных матриц сложность вычислений:
   • Обновление математических ожиданий $\mu_j$ ($j = \overline{1, k}$): $O(nkq)$,
   • Обновление ковариационных матриц $\Sigma_j$ ($j = \overline{1, k}$): $O(nkq)$,
   • Обновление весов кластеров $w_j$ ($j = \overline{1, k}$): $O(nk)$.
   Получаем, что последовательная сложность М-шага в случае недиагональных ковариационных матриц имеет порядок $O(nkq^2)$, а в случае диагональных ковариационных матриц — $O(nkq)$.

Таким образом, последовательная сложность итерации EM-алгоритма в случае недиагональных ковариационных матриц имеет порядок $O(kq^3 + nkq^2)$, а в случае диагональных ковариационных матриц — $O(nkq)$. При этом, обычно размерность элементов выборки $q$, также как и число кластеров $k$, значительно меньше числа элементов выборки $n$ ($k \ll n, q \ll n$), поэтому в случае недиагональных ковариационных матриц сложность может быть записана в виде $O(nkq^2)$.

1.7 Информационный граф

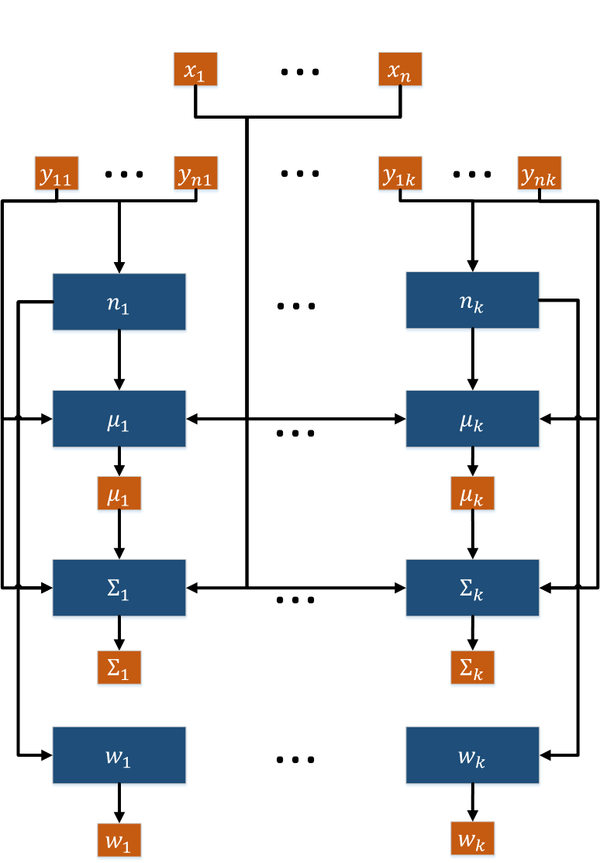
Граф алгоритма в терминах E-шагов и M-шагов представлен на рис. 1. Каждая итерация алгоритма зависит от результата работы предыдущей итерации, M-шаг зависит от результата E-шага.

Рисунок 1. Граф EM-алгоритма. $k$ — число кластеров; $X$ — множество наблюдений; $Y$ — матрица с вероятностями членства в кластерах.

Рассмотрим по отдельности информационные графы E-шага и M-шага.

1.7.1 E-шаг

Опишем граф E-шага как аналитически, так и в виде рисунка.

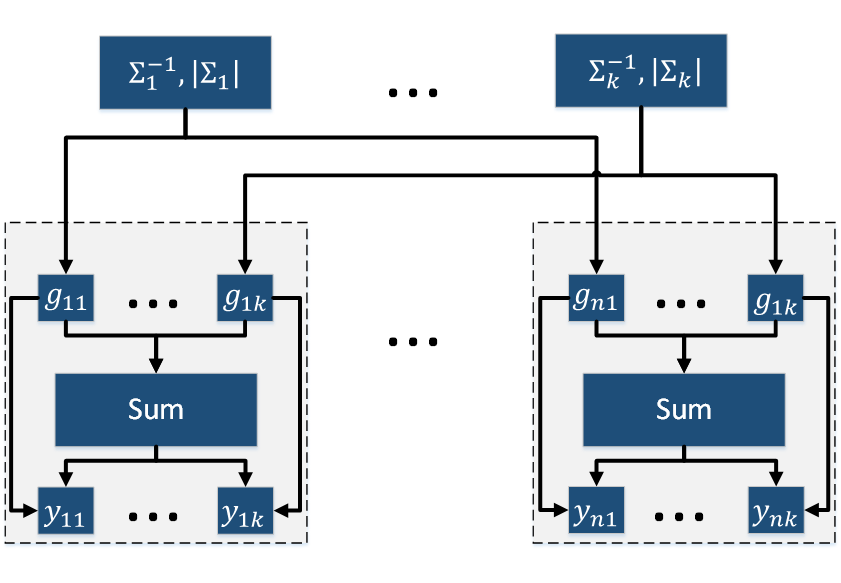
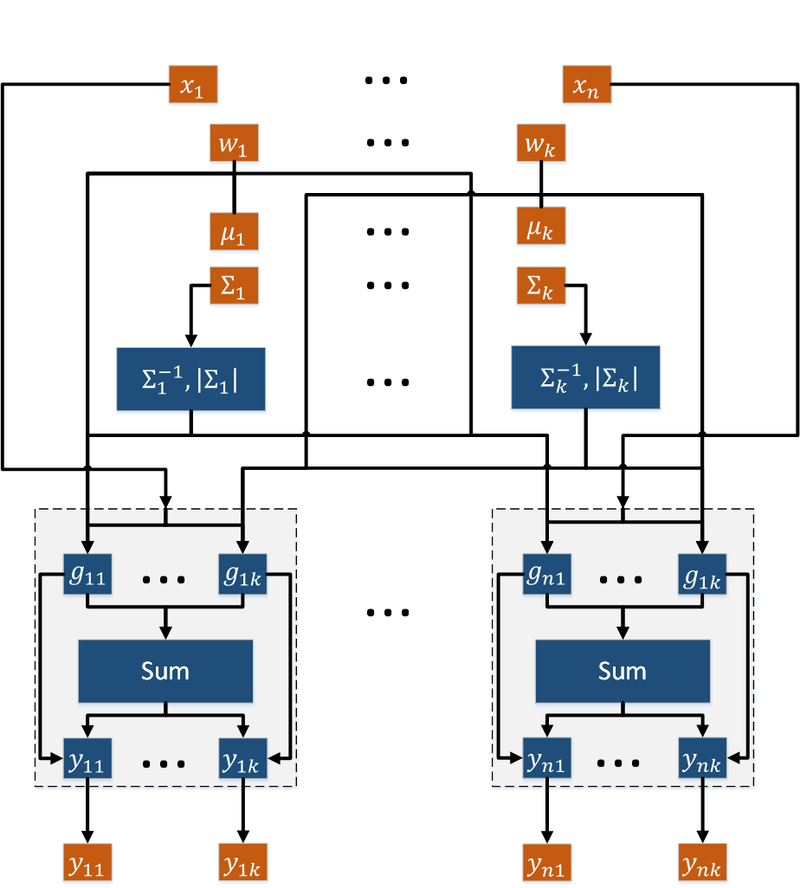
Граф алгоритма состоит из четырех групп вершин:

• Первая группа вершин соответствует вычислению обратных матриц и определителей ковариационных матриц. Число вершин: $k$. Аргументом этой операции является ковариационная матрица $\Sigma_j$. Результат срабатывания операции является промежуточным данным алгоритма.
• Вторая группа вершин соответствует вычислению $g_{ij} = \frac{w_j}{{2 \pi}^\frac{q}{2}|\Sigma_j|}\exp{\big\{-\frac{1}{2} \big( x_i - \mu_j \big)^T \Sigma_j^{-1} \big( x_i - \mu_j \big) \big\}}$. Число вершин: $nk$. Аргументами этой операции являются вес кластера $w_j$, математическое ожидание $\mu_j$, ковариационная матрица $\Sigma_j$, элемент выборки $x_i$. Результат срабатывания операции является промежуточным данным алгоритма.
• Третья группа вершин соответствует вычислению нормировочных коэффициентов $\sum_{l=1}^{k}g_{ij}$. Число вершин: $n$. Аргументами этой операции являются значения $g_{ij}, \, j = \overline{1, k}$. Результат срабатывания операции является промежуточным данным алгоритма.
• Четвертая группа вершин соответствует вычислению скрытых переменных $y_{ij}$. Число вершин: $nk$. Аргументами этой операции являются значение $g_{ij}$ и нормировочный коэффициент. Результат срабатывания операции является выходным данным алгоритма.

Описанный граф представлен на рис.2 и рис.3. Здесь вершины одной группы расположены в одной строке. Вершины-операции обозначены синим цветом, вершины-данные — оранжевым.

Рисунок 2. Граф E-шага.

Рисунок 3. Граф E-шага с с отображением входных и выходных данных.

1.7.2 M-шаг

Опишем граф M-шага как аналитически, так и в виде рисунка.

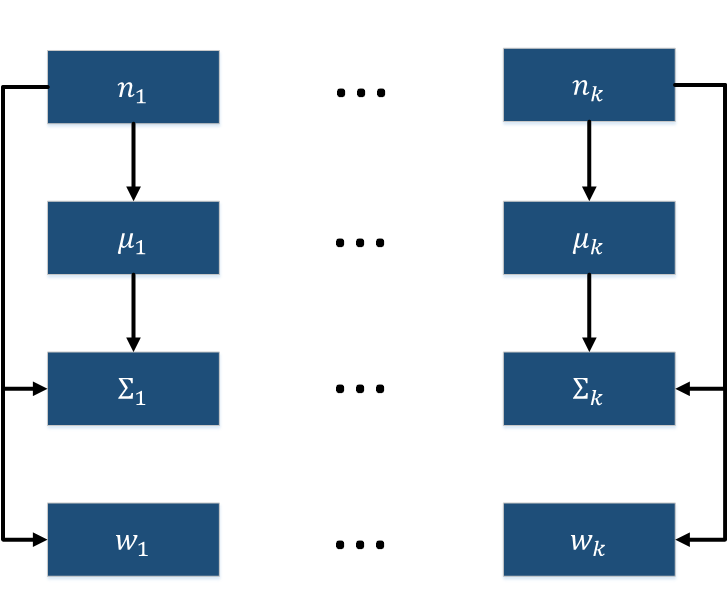
Граф алгоритма состоит из четырех групп вершин:

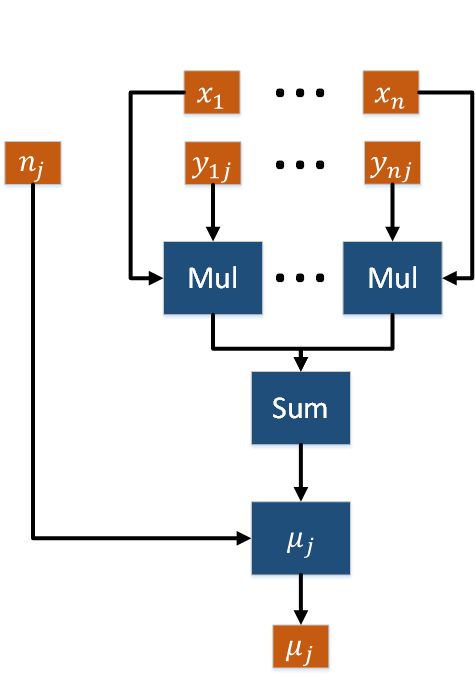
• Первая группа вершин соответствует вычислению нормировочных коэффициентов $n_j$. Число вершин: $k$. Аргументами этой операции являются скрытые переменные $y_{ij}, \, i = \overline{1, n}$. Результат срабатывания операции является промежуточным данным алгоритма.
• Вторая группа вершин соответствует вычислению математических ожиданий $\mu_j$. Число вершин: $k$. Аргументами этой операции являются множество наблюдений $X$, скрытые переменные $y_{ij}, \, i = \overline{1, n}$, нормировочный коэффициент $n_j$. Результат срабатывания операции является выходным данным алгоритма.
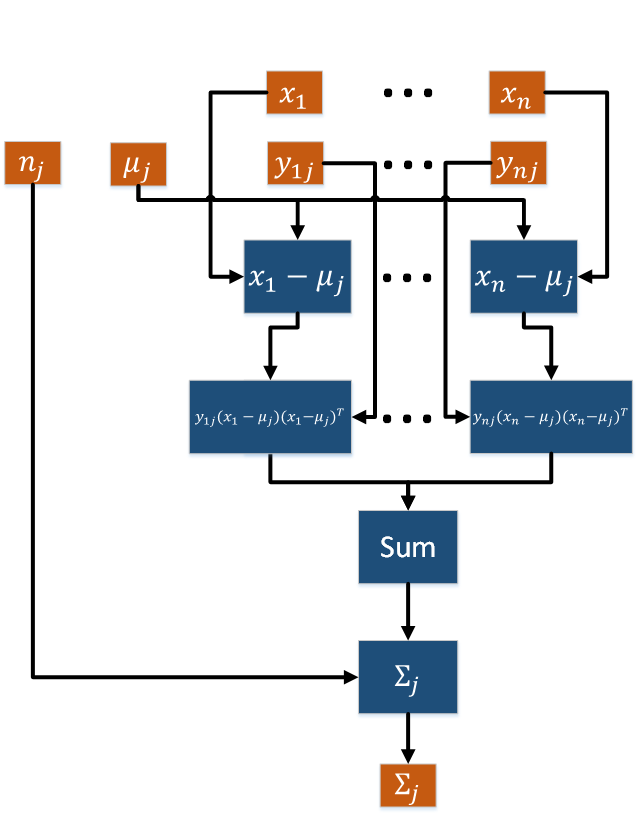
• Третья группа вершин соответствует вычислению ковариационных матриц $\Sigma_j$. Число вершин: $k$. Аргументами этой операции являются множество наблюдений $X$, скрытые переменные $y_{ij}, \, i = \overline{1, n}$, нормировочный коэффициент $n_j$, математическое ожидание $\mu_j$. Результат срабатывания операции является выходным данным алгоритма.
• Четвертая группа вершин соответствует вычислению весов кластеров $w_{j}$. Число вершин: $k$. Аргументом этой операции является нормировочный коэффициент $n_j$. Результат срабатывания операции является выходным данным алгоритма.

Описанный граф представлен на рис.4 и рис.5. Здесь вершины одной группы расположены в одной строке. Вершины-операции обозначены синим цветом, вершины-данные — оранжевым.

Рисунок 4. Граф M-шага.

Рисунок 5. Граф M-шага с отображением входных и выходных данных.

Графы вычисления математических ожиданий $\mu_j$ и ковариационных матриц $\Sigma_j$ представлены на рис. 6 и рис. 7.

Рисунок 6. Граф вычисления математического ожидания $\mu_j$.

Рисунок 7. Граф вычисления ковариационной матрицы $\Sigma_j$.

1.8 Ресурс параллелизма алгоритма

По графам из пункта 1.7 видно, что скрытые переменные $y_{ij}$ в E-шаге, $y_{ij}x_i$ в вычислении математических ожиданий $\mu_{j}$ и $y_{ij}(x_i - \mu_j)(x_i - \mu_j)$ в вычислении ковариационных матриц $\Sigma_{j}$ в M-шаге вычисляются независимо ($i = \overline{1, n}, \, j = \overline{1, k}$). Таким образом, при условии наличия неограниченного числа процессоров эти операции можно распараллелить как по числу наблюдений, так и по числу кластеров. Однако в отсутствии неограниченного числа процессорв целесообразно проводить распараллеливание по числу наблюдений, потому что, как правило, число наблюдений значительно больше числа кластеров ($n \gg q$).

При классификации по ширине ЯПФ его сложность будет $O(nk)$. Сложность ЯПФ при классификации по высоте зависит от способа вычисления обратных матриц и определителей ковариационных матриц, а также от способа суммирования при вычислении скрытых переменных и обновлении вектора параметров. Предположим, что размерность элементов выборки $q$ и число кластеров $k$ значительно меньше числа элементов выборки $n$ ($k \ll n, q \ll n$). Тогда вычисление обратных матриц и определителей ковариационных матриц можно не учитывать. Пусть для вычисления сумм используется пирамида сдваиванием. Тогда сложность суммирования при вычислении скрытых переменных равна $O(\log{k})$, а при обновлении вектора параметров — $O(\log{n})$. Следовательно, при классификации по высоте ЯПФ его сложность будет $O(\log{nk})$.

1.9 Входные и выходные данные алгоритма

Входные данные: $k$ — число кластеров; $X =\{x_{1}, x_{2}, ..., x_{n}\}$ — множество из $n$ наблюдений $q$-мерного пространства.

Объем входных данных: $nq + 1$.

Выходные данные: $(w, \theta) = (w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)$ — параметры смеси гауссовых распределений; $Y$ — матрица размера $n \times k$ с вероятностями членства в кластерах.

Объем выходных данных: $k(n + q^2 + q + 1)$.

1.10 Свойства алгоритма

Алгоритм является недетерминированным. Число итераций до сходимости метода зависит от начального приближения и выбранного критерия останова.

Предположим, что размерность элементов выборки $q$ и число кластеров $k$ значительно меньше числа элементов выборки $n$ ($k \ll n, q \ll n$), а число итераций до сходимости метода равно $m$. Тогда вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, имеет порядок $O\bigg(\frac{kq^2}{q + k}m\bigg)$.

1.10.1 Достоинства и недостатки алгоритма

Среди достоинств EM-алгоритма можно выделить следующие:

• Мощная статистическая основа.
• Линейное увеличение сложности при росте объема данных.
• Устойчивость к шумам и пропускам в данных.
• Возможность построения желаемого числа кластеров.
• Быстрая сходимость при удачной инициализации.

К недостаткам EM-алгоритма можно отнести следующее:

• Алгоритм неустойчив по начальным данным (то есть тем, которые инициализируют вектор параметров на первой итерации), так как он находит локальный экстремум, значение которого может оказаться гораздо ниже, чем глобальный максимум. В зависимости от выбора начального приближения алгоритм может сходиться к разным точкам. Также может сильно варьироваться скорость сходимости.
• Алгоритм не позволяет определять количество $k$ компонент смеси. Эта величина является структурным параметром алгоритма.
• Предположение о нормальности всех измерений данных не всегда выполняется.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Масштабируемость реализации алгоритма

Для исследования масштабируемости EM-алгоритм кластеризации был реализован с помощью технологии MPI. Была реализована версия алгоритма с диагональными матрицами ковариации. В качестве критерия останова было выбрано достижение максимального числа итераций (соответственно, вычисление логарифмического правдоподобия на каждой итерации не проводится).

Алгоритм параллельной реализации:

1. Распределение элементов выборки. Процесс 0 распределяет поровну элементы выборки по остальным процессам.
2. Инициализация параметров смеси гауссовых распределений. Процесс 0 инициализирует параметры и отправляет их остальным процессам. $\mu_j$ инициализируются случайными значениями в отрезке $[-1, 1]$, ковариационные матрицы $\Sigma_j$ определяются как единичные, веса $w_i$ кластеров задаются равными $\frac{1}{k}$.
3. Выполнение E-шага и M-шага алгоритма до достижения максимального числа итераций.
   1. E-шаг. Каждый процесс вычисляет значения скрытых переменных $y_{ij}$ по своему набору элементов выборки.
   2. M-шаг.
      1. Каждый процесс вычисляет суммы значений скрытых переменных $\sum_{i = 1}^{n\_proc_i}y_{ij}$ для каждого кластера $j = \overline{1, k}$ по своему набору элементов выборки и отправляет полученные суммы процессу 0. Процесс 0 вычисляет значения $n_j$ по полученным суммам и отправляет их остальным процессам. Каждый процесс обновляет значения $w_j$ по полученным значениям $n_j$.
      2. Каждый процесс вычисляет суммы $\sum_{i = 1}^{n\_proc_i}y_{ij}x_i$ для каждого кластера $j = \overline{1, k}$ по своему набору элементов выборки и отправляет полученные суммы процессу 0. Процесс 0 вычисляет суммы $\sum_{i = 1}^{n}y_{ij}x_i$ для каждого кластера $j = \overline{1, k}$ по всем элементам выборки и отправляет их остальным процессам. С помощью полученных сумм каждый процесс вычисляет значения математических ожиданий $\mu_j$.
      3. Каждый процесс вычисляет суммы $sum_l = \sum_{i = 1}^{n\_proc_i}y_{ij}(x_{il} - \mu_{jl}^{new})^2 \, (l = \overline{1, q})$ для каждого кластера $j = \overline{1, k}$ по своему набору элементов выборки и отправляет полученные суммы процессу 0. Процесс 0 вычисляет суммы $sum_l = \sum_{i = 1}^{n}y_{ij}(x_{il} - \mu_{jl}^{new})^2 \, (l = \overline{1, q})$ для каждого кластера $j = \overline{1, k}$ по всем элементам выборки и отправляет их остальным процессам. С помощью полученных сумм каждый процесс вычисляет значения диагональных элементов матриц ковариации $\Sigma_j$.

Распараллеливание было проведено по числу элементов выборки, поэтому и исследование масштабируемости было проведено для числа элементов выборки. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессов [8 : 128] с шагом 8;
• число элементов выборки [1000000 : 20000000] с шагом 1000000;
• размерность элементов выборки 4;
• число кластеров 4;
• число итераций 50.

Для каждого набора параметров измерялось среднее время выполнения одной итерации алгоритма. На следующем рисунке приведен график производительности данной реализации EM-алгоритма кластеризации в зависимости от изменяемых параметров запуска.

Рисунок 8. Параллельная реализация EM-алгоритма кластеризации. Изменение производительности в зависимости от числа процессов и числа элементов выборки.

Исследованная параллельная MPI-реализация на языке C

2.7 Существующие реализации алгоритма

1. OpenCV;
2. Armadillo — OpenMP реализация с предположением диагональности ковариационных матриц;
3. MLPack;
4. scikit-learn;
5. Matlab;
6. CUDA реализация №1;
7. CUDA реализация №2.

3 Литература

<references \>