Участник:Chist/Метод Ньютона

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.

Поскольку функция может иметь несколько корней, чтобы попытаться найти их все, необходимо провести перебор начальных приближений. При нас интересуют не только действительные корни, но и комплексные, будет производить перебор по некоторой сетке на комплексной плоскости.

1.2 Математическое описание алгоритма

Пусть задана некоторая функция [math]\ f(x) [/math], её производная [math]\ f'(x) [/math] и сетка на комплексной плоскости вида

[math] z_0 = \left( x_0 + \alpha \dfrac{x_1 - x_0}{N} \right) + i \cdot \left( y_0 + \beta \dfrac{y_1 - y_0}{M} \right), \qquad \alpha = \overline{1, N},\ \beta = \overline{1, M}, [/math]

где [math]\ i [/math] — мнимая единица.

Получим решения уравнения [math]\ f(z) = 0 [/math] с помощью итерационного процесса, определяемого формулой:

[math] z_{k+1} = z_k - \dfrac{f(z_k)}{f'(z_k)}, [/math]

где в качестве начального приближения [math]\ z_0[/math] перебираются всевозможные точки рассмотренной сетки.

1.2.1 Теоретическое обоснование

Пусть [math]\ F(x)[/math] — оператор, отображающий линейное нормированное пространство [math]H[/math] на линейное нормированное пространство [math]Y[/math]. Линейный оператор [math]P[/math], действующий из пространства [math]H[/math] в пространство [math]Y[/math], назовём производной оператора [math]F(x)[/math] в точке [math]x[/math], если

[math] \| F(x + \eta) − F(x) − P\eta \|_Y = o(\| \eta \|_H). [/math]

Будем обозначать такой оператор [math]P[/math] как [math]F′(x)[/math].

Пусть [math]\ X[/math] — решение уравнения [math]F(X) = 0[/math], [math]\ \Omega_a = \{ x: \| x - X \| \lt a \}[/math]. Пусть также при некоторых [math]a \gt 0,\ a_1 \ge 0,\ a_2 \le \infty[/math] выполнены условия:

[math]\label{requirement_one} \| (F'(X))^{-1} \|_{Y} \le a_1 \text{ при } x \in \Omega_a, [/math]

[math] \| F(u_1) - F(u_2) - F'(u_2)(u_1 - u_2) \|_{Y} \le a_2 \|u_2 - u_1 \|_{H}^{2} \text{ при } u_1, u_2 \in \Omega_a. [/math]

Обозначим [math]c = a_1 a_2[/math], [math]b = \min \{a, c^{-1}\}[/math].

Метод Ньютона применим на основании следующей теоремы:

Теорема. Если выполнены указанные условия и начальное приближение [math]x_0[/math] принадлежит [math]\Omega_b[/math], то итерационный процесс Ньютона

[math] x_{n + 1} = x_{n} - (F'(x_n))^{-1} F(x_n) [/math]

сходится с оценкой погрешности

[math] \| x_n - X \|_{H} \le c^{-1} \left( c \| x_0 - X \|_{H} \right)^{2^n}. [/math]

Доказательство этой теоремы можно найти в литературе.

1.3 Вычислительное ядро алгоритма

Вычислительную сложность алгоритма представляют операции вычисления значения функций в заданной точке, а так же операции вычитания и деления. При этом итерационный процесс запускается [math]N \cdot M[/math] раз, а количество итераций в каждом процессе, вообще говоря, не определено; наиболее популярными условиями останова являются следующие:

[math] \| z_{n + 1} - z_{n} \| \lt \varepsilon, [/math]

[math] | f(z_{n}) | \lt \varepsilon. [/math]

Однако, для верхней оценки числа операций удобно зафиксировать число итераций в каждом процессе. Это так же позволит завершить вычисления в случае, если итерационный процесс не сходится.

1.4 Макроструктура алгоритма

Для обеспечения параллелизма сперва исходная сетка разбивается на [math]n[/math] по возможности равных участков (например, на полосы длины [math]M[/math]) — запускается [math]n[/math] процессов. В каждом участке последовательно запускаются итерационные процессы для каждого узла сетки, в ходе которых:

• 1. вычисляются значения функций [math]\ f(z_k)[/math], [math]\ f'(z_k)[/math] (предполагается, что функции заданы аналитически);
• 2. вычисляется следующая точка:

[math] z_{k+1} = z_k - \dfrac{f(z_k)}{f'(z_k)}; [/math]

• 3. если условие останова не выполнено, переходим к шагу 1.

Поскольку полученные в каждом процессе результаты необходимо обработать (проверить, являются ли полученные числа корнями; также желательно оставить только уникальные решения), нужно переслать полученные данные в какой-то один процесс. Проверку корней можно осуществлять на том процессоре, где они были получены, но это вызовет дополнительные сложности при работе с памятью во время последующей пересылки.

1.5 Схема реализации последовательного алгоритма

Последовательный алгоритм является частным случаем описанного алгоритма при [math]n = 1[/math].

1.6 Последовательная сложность алгоритма

Для определения сложности алгоритма, необходимо выбрать класс функций, для которого будет написана программа (предполагается, что функции [math]\ f(x) [/math], [math]\ f'(x) [/math] заданы аналитически). Проведём исследование для многочленов степени [math]p[/math], каждый из которых определяется вектором из [math]p + 1[/math] коэффициентов. Пусть выбран критерий останова, при котором каждое использование метода Ньютона включает в себя [math]iter\_num[/math] операций.

Основную вычислительную сложность представляют собой операции умножения и деления комплексных чисел с плавающей точкой, будем считать их суммарное количество. Однако, необходимо помнить, что операции над комплексными числами требуют больше ресурсов, чем операции над действительными числами.

Для вычисления значения многочлена степени [math]p[/math] в точке с помощью тривиального алгоритма необходимо [math]\frac{p(p+1)}{2} + p[/math] операций умножения. Воспользовавшись схемой Горнера, можно сократить число умножений до [math]p[/math]:

[math] P(x) = ( \ldots (a_p x + a_{p-1}) x + a_{p-2})x + \ldots + a_1)x + a_0. [/math]

В каждой итерации метода нужно вычислить не только значение многочлена в точке, но и значение его производной в этой точке. Это добавляет ещё [math]p - 1[/math] операцию. Наконец, в каждой итерации производится ровно одно деление.

Учитывая количество узлов сетки и заданное количество итераций, получим общее число операций умножения деления:

[math] p + N \cdot M \cdot iter\_num \cdot (p + (p - 1) + 1) = p + 2 \cdot N \cdot M \cdot iter\_num \cdot p, [/math]

где первое слагаемое соответствует числу операций для вычисления коэффициентов производной многочлена.

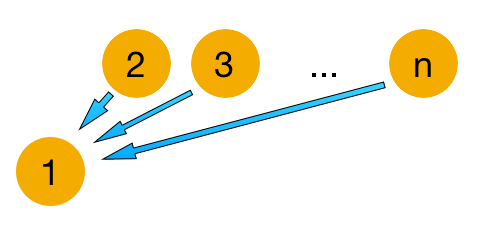
1.7 Информационный граф

Пересылка данных происходит от каждого процесса к первому. При этом в первом процессе так же происходят вычисления, поэтому может возникнуть задержка при пересылке данных, если вычисления в первом процессе ещё не завершены. Однако выделять под обработку пересланных данных отдельный процесс нерационально: в таком случае на нём будет застой во время вычислений на всех остальных процессах.

Рисунок 1. Граф алгоритма.

При этом первый процесс не пересылает свои данные к себе (в привычном понимании пересылки), а просто сохраняет полученные результаты в отдельный массив.

1.9 Входные и выходные данные алгоритма

Входные данные:

• [math]p + 1[/math] действительное число — коэффициенты многочлена.
• Действительные числа [math]x_0[/math], [math]y_0[/math], [math]x_1[/math], [math]y_1[/math], определяющие левый нижний [math](x_0, y_0)[/math] и правый верхний [math](x_1, y_1)[/math] узлы прямоугольной сетки.
• Натуральные числа [math]M[/math] и [math]N[/math], задающие количество узлов сетки по горизонтали и вертикали
• Натуральное число [math]iter\_num[/math], равное количеству итераций при каждом запуске метода Ньютона

Выходные данные:

• список всех найденных комплексных чисел [math]z[/math], удовлетворяющих условию [math]|f(z)| \lt \varepsilon[/math].

1.10 Свойства алгоритма

Как хорошо видно, соотношение последовательной и параллельной сложности является линейным.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, так же является линейной.

Очевидно, что алгоритм является детерминированным.

Как уже было замечено, могут возникнуть задержки в связи с пересылкой данных от каждого процесса к первому. Это связано не только с тем, что в первом процессе так же происходят вычисления, но и с тем, что несколько процессов могут отправить запросы на пересылку одновременно. В результате может возникнуть неоптимальное использование мощностей.

2 Программная реализация алгоритма

2.3 Возможные способы и особенности параллельной реализации алгоритма

Основная идея параллелизма заключается в разбиении сетки на [math]n[/math] участков. Идеи параллелизма можно также применять при вычислении значения многочлена в точке, однако это становится нерациональным при использовании схемы Горнера. Стоит отметить, что, за исключением перебора по сетке, в алгоритме нет каких-либо циклов.

2.8 Существующие реализации алгоритма

• Последовательные реализации
  • ALIAS C++. Язык реализации - C++. Распространяется бесплатно, исходные коды и примеры использования можно скачать на сайте.
  • Numerical Recipes. Язык реализации - C++. Исходный код можно найти в секции 9.7 книги Numerical recipes(third edition). Бесплатно доступны предыдущие издания для языков C, Fortran77, Fortran90.
  • Sundials. Язык реализации - C, также есть интерфейс для использования в Fortran-программах. Распространяется по лицензии BSD.
  • Numerical Mathematics- NewtonLib. Язык реализации - C, Fortran. Исходные коды доступны в качестве приложения к книге Peter Deuflhards "Newton Methods for Nonlinear Problems -- Affine Invariance and Adaptive Algorithms".
  • PETSc. Язык реализации - C, есть интерфейс для Java и Python. Распространяется по лицензии BSD.

• Параллельные реализации
  • Sundials. Язык реализации - C, также есть интерфейс для использования в Fortran-программах. Распространяется по лицензии BSD.
  • PETSc. Язык реализации - C, есть интерфейс для Java и Python. Распространяется по лицензии BSD.

3 Литература

<references \>