Участник:Gkhazeeva/Нечеткий алгоритм C средних

Нечеткий алгоритм C средних
Последовательный алгоритм
Последовательная сложность	$O(Mdc^2i)$, $i$ - количество итераций
Объём входных данных	$M*d$, [количество наблюдений * размерность]
Объём выходных данных	$M*c$, [количество наблюдений * количество кластеров]
Параллельный алгоритм
Высота ярусно-параллельной формы
Ширина ярусно-параллельной формы

Авторы : Гелана Хазеева, Павел Юшин

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Кластеризация - это объединение объектов в группы (кластеры) на основе схожести признаков для объектов одной группы и отличий между группами. Нечеткий алгоритм C Средних (Fuzzy C-means, FCM) - алгоритм кластеризации, позволяющий объектам принадлежать с различной степенью нескольким кластерам одновременно. Впервые алгоритм был предложен J.C. Dunn в 1973 . Нечеткое разбиение позволяет просто решить проблему объектов, расположенных на границе двух кластеров - им назначают степени принадлежностей равные 0.5.

Входные данные алгоритма: набор векторов, которые следует кластеризовать.

Параметры алгоритма: $c$ - количество кластеров; $m$ - экспоненциальный вес; $\varepsilon$ - параметр останова алгоритма.

Выходные данные: матрица вероятностей принадлежности векторов кластерам.

Краткое описание алгоритма:

• Задать параметры алгоритма.

• Сгенерировать случайную матрицу принадлежностей векторов кластерам (матрицу нечеткого разбиения).

• Повторить следующие шаги до момента, пока матрицы нечеткого разбиения на этом и предыдущем шаге алгоритма будут отличать менее чем на параметр останова.
  • Рассчитать центры кластеров.
  • Рассчитать расстоение между объектами и центрами кластеров.
  • Пересчитать элементы матрицы нечеткого разбиения.

1.2 Математическое описание алгоритма

Пусть $W = w_{ij} \in[0,1],\; i = 1, ..., M, \; j = 1, ..., c$ - матрица разбиения, где $w_{i,j}$ - степень принадлежности объекта $i$ к кластеру $j$; $c$ - количество кластеров, $M$ - количество векторов.

При этом элементы матрицы должны удовлетворять условиям:

• $\sum_{j = 1}^c w_{ij} = 1, i = 1, ..., M$ $(1)$
• $0 \lt \sum_{i = 1}^M w_{ij} \lt M, j = 1, ..., c$ $(2)$

Тогда алгоритм принимает следующий вид:

1) Задаем параметры алгоритма: $c$ - количество кластеров; $m \gt = 1$ - экспоненциальный вес, определяющий нечеткость кластеров; $\varepsilon \gt 0$ - параметр останова алгоритма.

2) Генерируем случайным образом матрицу нечеткого разбиения с учетом условий $(1)$ и $(2)$

3) Рассчитываем центроиды (центры кластеров): $V_j = {{\sum_{i=1}^M w_{ij}^m * X_i} \over {\sum_{i=1}^M w_{ij}^m}}, j = 1, ..., c$

4) Рассчитываем расстояния между объектами $X$ и центроидами:

$D_{ij} = {||X_i - V_j||}, i = 1,...,M; j = 1,...,c$

5) Пересчет элементов матрицы разбиения:

при $D_{ij} \gt 0$ : $w_{ij} = {{1}\over {{ (\sum_{k=1}^c {{D_{ij}}\over{D_{ik}}} ) }^{2/(m-1)}}}, j = 1,...,c$

при $D_{ij} =0$ : $w_{ij} = \delta_{ij}, j = 1,...,c$, где $\delta_{ij}$ - символ Кронекера

6) Если $|| F - F^{*} || \lt \varepsilon$, где $F^{*}$ - матрица нечеткого разбиения предыдущей итерации, то идем далее, иначе возвращаемся на пункт 3.

7) Конец.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма являются пункты (3), (4), (5) - расчет центроидов, вычисление расстояний и пересчет элементов матрицы соответственно

1.4 Макроструктура алгоритма

Основные шаги при реализации алгоритма

• Генерация случайной матрицы размера $M$ на где $c$, проверка условий
• Расчет центроидов – по сути, скалярное произведение с нормировкой
• Расчет расстояний – в общепринятом случае является скалярным произведением
• Пересчет матрицы – по сути, скалярное произведение
• Проверка условий останова – вычисление нормы

1.5 Схема реализации последовательного алгоритма

   float ** FuzzyCMeans (float** X, c, m, eps){
       n = X.size();
       r = X[0].size();
       centers = generateZeroFill(c, r)
       Wprev = genetateRandFill(n, c);
       W = Wprev;
       while (true){
           // обновляем центры кластеров 
           for (int i=0; i<c; i++){
               float * num = new float []();
               float den = 0;
               for (int j=0; j<n; j++){
                   num += pow(W[j][i], m) * X[j];
                   den+=pow(W[j][i], m);
               }
               centers[i] = num / den;
           }
           //обновляем вероятности W и считаем расстояние между матрицами W и Wprev
           float max_diff = 0;
           for (int i=0; i<n; i++)
               for (int j=0; j<c; j++){
                   total = 0;
                   for (int m=0; m<с; m++)
                       total += pow(distance(X[i], centers[j]) / distance(X[i], centers[m]), 2/(m-1));
                   W[i][j] = 1/total;
                   max_diff = max(abs(Wprev[i][j]-W[i][j]), max_diff);
                   Wprev[i][j] = W[i][j];
              }               
          if (max_diff < eps):                
               break;
       }
       return W;
   }

1.6 Последовательная сложность алгоритма

Последовательная сложность алгоритма состоит из сложности каждой итерации умноженной на их количество. Так как число итераций заранее неизвестно и зависит от входных параметров, рассмотрим сложность на каждой итерации. Наибольшую сложность представляет собой пересчет матрицы, сложность которого $O(c^2 nd)$ (по сравнению со сложностью $O(cnd)$ расчета расстояний, вычисления центроидов и проверки условия останова). Итого общая сложность алгоритма $O(c^2 ndi)$

1.7 Информационный граф

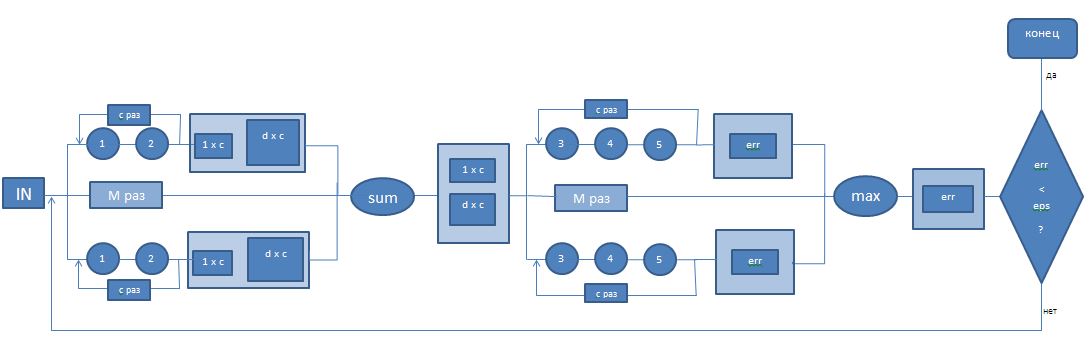
Информационный граф представлен на рисунке ниже.

Первый ярус состоит из $M$ параллельных операций 1, 2, совершаемых в цикле $c$ раз для каждого кластера. Операция 1: $w_{ij}^m$, где $j$ - номер итерации в цикле, $i$ - номер параллельной ветви.

Операция 2: $w_{ij}^m*X_i$

Здесь $j$ - номер итерации в цикле, $i$ - номер параллельной ветви.

На выходе из каждой ветки получаем вектор размера $1$ x $c$ и матрицу размера $d$ x $c$. Далее совершаем поэлементное сложение векторов и матриц соответственно, а затем делим каждый столбец в матрице на соответствующий элемент в векторе.

Второй ярус состоит их $M$ параллельных операций 3, 4, 5 также совершаемых в цикле $c$ раз.

Операция 4: обновление значения $w_{ij}$ по указанной в разделе 1.2 в пункте 5 формуле.

Операция 5: $maximum = max(|w_{ij} - w_{ij}^{prev}|, maximum)$.

Операция 6: $w_{ij}^{prev} = w_{ij}$.

Здесь $j$ - номер итерации в цикле, $i$ - номер параллельной ветви.

На выходе из каждой ветки получаем число $maximum$. Далее находим максимальное значение из полученных величин для каждой ветки. Затем проверяем условие останова алгоритма.

1.9 Входные и выходные данные алгоритма

• Входные данные алгоритма: набор векторов $x_i$ размерности $d$, где $i = 1,...,M$; $M$ - количество векторов.
• Выходные данные алгоритма: матрица вероятностей принадлежности векторов кластерам $M$ на $c$.

1.10 Свойства алгоритма

• Соотношение последовательной и параллельной формы алгоритма: ${xz} \over {xz}$
• Вычислительная мощность: ${dc^2i} \over {c+d}$.
• Устойчивость: алгоритм не является устойчивым, поэтому существует много исследований о том, как первоначально выбрать параметры кластеризации.
• Сбалансированность: в данном алгоритме операция умножения доминирует над операцией сложения. Операции между параллельными ветвями сбалансированны.
• Детерминированность: алгоритм не является детерминированным, так как матрица нечеткого разбиение генерируется произвольно.
• Степень исхода вершины информационного графа ( для одной интерации): 2 (3 - с учетом, если выходные данные пошли на следующую итерацию).

2 Программная реализация алгоритма

2.2 Существующие реализации алгоритма

• Реализация алгоритма на POSTGRESQL: http://num-meth.srcc.msu.ru/zhurnal/tom_2012/pdf/v13r207.pdf
• Библиотека для MATLAB: http://www.mathworks.com/help/fuzzy/fcm.html (распространяется на коммерческой основе)