Участник:Elena777mc/Плотностный алгоритм кластеризации DBSCAN

Плотностный алгоритм кластеризации DBSCAN
Последовательный алгоритм
Последовательная сложность	[math]O(n \log n)[/math]
Объём входных данных	[math]n[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(|X| \log |X|)[/math]
Ширина ярусно-параллельной формы	[math]O(m)[/math]

Основные авторы описания: Малахова Е.С., Сагиолданова Ж.

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Кластеризация – это процесс разбиения множества с [math]N[/math] элементами [math]x_1, x_2, ... , x_n (x_n[/math] имеет размерность [math]m[/math]) на [math]K[/math] кластеров, так, чтобы в каждом кластере все элементы были схожи в каком-то смысле. [math]x_i[/math] могут быть числовыми, категориальными или смешанными данными. В плотностных методах кластеры рассматриваются как регионы пространства данных с высокой плотностью объектов, которые разделены регионами с низкой плотностью объектов.

Алгоритм DBSCAN (Density Based Spatial Clustering of Applications with Noise) –плотностной алгоритм для кластеризации пространственных данных с присутствием шума, был предложен Мартином Эстер, Гансом-Питером Кригель и их коллегами в 1996 году как решение проблемы разбиения (изначально пространственных) данных на кластеры произвольной формы.

Большинство алгоритмов, производящих плоское разбиение, создают кластеры по форме близкие к сферическим, так как минимизируют расстояние точки до центра кластера

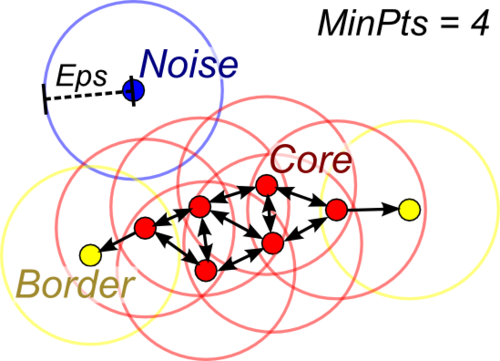
Авторы DBSCAN экспериментально показали, что их алгоритм способен распознать кластеры различной формы. Идея, положенная в основу алгоритма, заключается в том, что внутри каждого кластера плотность точек (объектов) заметно выше, чем плотность снаружи кластера, а также плотность в областях с шумом ниже плотности любого из кластеров. Еще точнее, для каждой точки кластера ее окрестность в диапазоне заданного радиуса должна содержать не менее некоторого числа точек, которое задается пороговым значением.

1.2 Математическое описание алгоритма

Рис. 1. Пример ядровых, граничных и шумовых точек алгоритма

Исходные данные: объекты, которые нужно кластеризовать, параметры [math]MinPts, \ \varepsilon[/math] . Между объектами можно считать расстояния.

Вычисляемые данные: разбиение объектов по кластерам. Количество кластеров зависит от исходных данных.

Для построения оценки плотности, на основе соседства точек вводятся понятия достижимости и связности. Под [math]\varepsilon [/math] -соседями точки [math]x \in X[/math] понимается множество точек, расстояние до которых не превышает [math]\varepsilon [/math], т. е. [math]N_\varepsilon (x) = \{y \in X | D(x, y) \le \varepsilon\}[/math]. Тогда точка [math]y[/math] достижима из точки [math]x[/math], если существует последовательность точек [math]x^{(1)}=x, x^{(2)},... , x^{(p-1)}, x^{(p)}=y[/math], для которой выполнено:

[math] \begin{align} x^{(i+1)} \in N_\varepsilon (x^{(i)}), i=1,... ,p-1 \\ \mid N_\varepsilon (x^{(i)}) \mid \ge MinPts, i=1,... ,p-1 \end{align} [/math]

Здесь значение [math]MinPts[/math] задаётся пользователем и регулирует порог «шума». Согласно второму условию, у точек, находящихся внутри кластера, должно быть не менее [math]MinPts \ \varepsilon[/math] -соседей. Такие точки называются «ядрами». Остальные точки разделяются на граничные (имеющие менее [math]MinPts \ \varepsilon [/math] -cоседей, но достижимые из какого-либо «ядра») и шумовые. Две точки связны, если существует «ядро», из которого они обе достижимы. При такой постановке задачи, под кластером понимается максимальное связное подмножество множества [math]X[/math] . Точки, не попавшие в какой-либо кластер (не принадлежащие [math]\varepsilon[/math] -окрестности какого-либо «ядра»), относятся к классу «шум».

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является нахождение [math]\varepsilon[/math]-соседей каждого объекта входного множества [math]X[/math]. На эту часть алгоритма приходится основное время работы алгоритма, так как требуется найти всех соседей для каждого объекта заданного множества.

1.4 Макроструктура алгоритма

Алгоритм DBSCAN использует пространственную структуру данных для определения соседних объектов. Это может быть R*-дерево или kd-дерево. Такие структуры данных позволяют найти все объекты в пределах определенного расстояния от текущего объекта. Сложность построения таких структур [math]O(n \log n)[/math] и использование такой структуры не увеличит сложность всего алгоритма (если сложность самого алгоритма [math]O(n \log n)[/math]). Также для построения этих деревьев нужно уметь находить расстояние между объектами [math]\rho(u,v)[/math], в, это расстояние можно вводить разными способами. Например, если [math]\rho(u,v)[/math] - метрика в евклидовом пространстве, [math]u=(u_1,...,u_n)[/math] и [math](v_1,...,v_n)[/math], то расстояние вычисляется следующим образом: [math]\rho(u,v)=\sqrt{(u_1-v_1)^2+(u_2-v_2)^2+...+(u_n-v_n)^2} = \sqrt{\sum_{k=1}^n(u_k-v_k)^2}[/math]

1.5 Схема реализации последовательного алгоритма

Последовательная реализация алгоритма может быть представлена следующим псевдокодом:

[math]DBSCAN(X, \varepsilon, MinPts)[/math]
//Изначально все объекты в [math]X[/math]не кластеризованы
   [math]FORALL[/math]  objects  [math]x[/math] in [math]X\  DO[/math]
      [math]IF\  x[/math] is unclassified
        call function [math]expand\_cluster[/math] to construct a cluster wrt. [math]\varepsilon[/math] and [math]MinPts[/math] containing [math]x[/math]

[math]FUNCTION\ expand\_cluster(x,X,\varepsilon, MinPts):[/math]
   [math]retrive\_\varepsilon neighborhood(x, \varepsilon)[/math];
   [math]IF \mid N_{\varepsilon}(x) \mid \lt  MinPts[/math] //т.е. [math]x[/math] - не ядровой объект
      mark [math]x[/math] as [math]noise[/math]  and [math]RETURN[/math];
   [math]ELSE[/math]//т.е. [math]x[/math] - ядровой объект
      select a new cluster-id and mark all objects in [math]N_{\varepsilon}(x)[/math] with this current [math]cluster-id[/math]; 
      push all objects from [math]N_{\varepsilon}(x)[/math]\[math](x)[/math] onto the stack seeds;
      [math]WHILE\ NOT[/math] seeds.empty() [math]DO[/math] 
        [math]currentObject[/math] := seeds.top();
        seeds.pop();
        [math]retrive\_\varepsilon neighborhood(currentObject, \varepsilon)[/math];
        [math]IF \mid N_{\varepsilon}(currentObjects) \mid \ge MinPts[/math]
          select all objects in [math]N_{\varepsilon}(currentObject)[/math] not yet classified or marked as [math]noise[/math],
          push the unclassified objects onto seeds and mark all of these objects with current [math]cluster-id[/math];
    [math]RETURN[/math]

[math]FUNCTION\ retrive\_\varepsilon neighborhood(x, \varepsilon)[/math] //функция возвращает соседей на основе пространственной структуры данных
  return [math]\{ x' \ | \ \forall x' \in X: \rho(x, x') \lt  \varepsilon \}[/math]

1.6 Последовательная сложность алгоритма

Для того, чтобы алгоритм мог кластеризовать все объекты, необходимо пройти по каждому из них хотя бы один раз. Если использовать специальную пространственную структуру данных для определения соседних объектов со сложностью [math]O(\log n)[/math], то сложность алгоритма [math]O(n \log n)[/math]. Если не использовать пространственную структуру данных, то в худшем случае алгоритм будет иметь сложность [math]O(n^2)[/math], так как придется считать полную матрицу расстояний между объектами.

1.7 Информационный граф

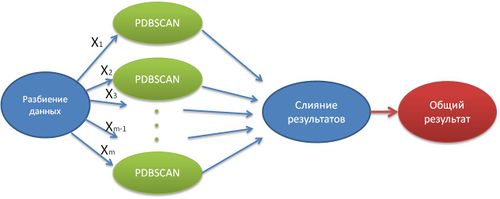
В настоящем алгоритме осуществляется параллелизм по данным. Ниже представлена общая структура данного алгоритма.

Рис.1. Общая информационная структура алгоритма

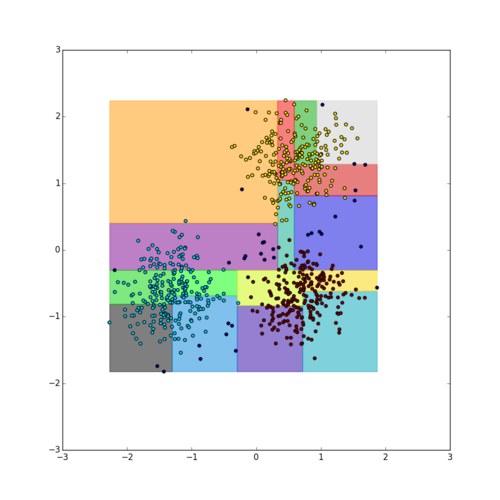
Разбиение данных происходит с помощью пространственной структуры данных (R*-дерево, kd-дерево), которая разбивает все множество объектов [math]X[/math] на [math]m[/math] частей: [math]X_1,X_2,...,X_m[/math].

Рис.2. Пример разбиения объектов на части на основе пространственной структуры

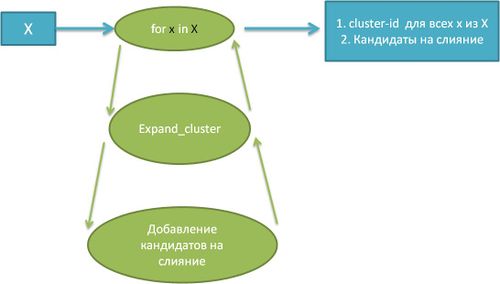
Далее на каждой части объектов применяется алгоритм PDBSCAN (каждая часть использует пространственную структуру данных, которая распределяется вместе с каждой частью данных), структура которого представлена ниже.

Рис.3. Информационная структура алгоритма PDBSCAN

Данный алгоритм отличается от общего алгоритма DBSCAN тем, что применяется к части объектов и для каждой из этих частей определяет кандидатов на слияние. Если для ядрового объекта части [math]X_i[/math] в [math]\varepsilon[/math]-окрестности находится объект из другой части [math]X_j[/math], то такие объекты становятся кандидатами на слияние.

Само слияние осуществляется следующим образом: для каждой пары кандидатов на слияние, объединяем кластеры, соответствующие этим кандидатам в один общий кластер.

1.8 Ресурс параллелизма алгоритма

Как видно из общей структуры графа алгоритма, ширина ярусно-параллельной формы алгоритма [math]O(m)[/math], где m - количество частей, на которые разбиваются все входное множество объектов [math]X[/math]. Высотой ярусно-параллельной формы алгоритма является [math]O(|X| \log |X|)[/math], где [math]\mid X \mid[/math] - максимальное количество среди числа объектов в каждой части разбиения. Именно такую сложность имеет алгоритм PDBSCAN, применяемый к каждой отдельной части разбиения.

1.9 Входные и выходные данные алгоритма

Входной информацией является множество точек X из n-мерного пространства, на котором определена функция расстояния D. В наиболее распространенном случае пространственной кластеризации используется Евлидова метрика между векторами из \mathb{R}^n.

Выходом алгоритма является размеченное множество точек X, в котором каждой точке соответствует номер ее кластера. Обычно каждой точке из X сопоставляется ее номер, а на выходе алгоритм дает отображение номеров точек в номера соответствующих им кластеров, например в виде вектора размера |X|

1.10 Свойства алгоритма

Вычислительная мощность, как отношение числа операций к суммарному объему входных и выходных данных линейна.

1.10.1 Преимущества алгоритма

1. алгоритм может обрабатывать большой объем данных и не зависит от порядка ввода данных;
2. может определять кластера произвольной формы;
3. параллельная реализация сбалансирована по количеству и виду производимых операций (вычисление расстояния, сравнение с \varepsilon);
4. не требуется задание числа кластеров;
5. может выделять кластеры в присутствии «шума»и выбросов;
6. число итераций определяется заранее

1.10.2 Недостатки алгоритма

1. не может выделять кластеры сложной структуры, например, имеющие разную плотность, так как параметры алгоритма не могут быть выбраны отдельно для каждого кластера;
2. не может построить иерархическую структуру кластеров;
3. не детерминирован, так как граничные точки, достижимые из более, чем одного кластера, могут быть частью любого из них в зависимости от порядка обрабатываемых данных. Однако такая ситуация возникает редко, а относительно ядровых точек и шума DBSCAN детерминирован.

2 Программная реализация алгоритма

2.2 Существующие реализации алгоритма

• Scikit learn (Python, последовательная реализация)
• Northwestern University (C++, параллельная реализация kd-tree)
• github/ContinuumIO (Python, параллельная реализация)
• github/propanoid (C++, последовательная реализация VP tree)
• github/dparks1134 (С++, последовательная реализация)
• Disjoint-Set Data Structure based Parallel DBSCAN (C++ параллельная реализация kd-tree)
• github/bwoneill (Spark/Python параллельная реализация kd-tree)
• github/alitouka (Spark/Scala параллельная реализация)
• CRAN (R, последовательная реализация)
• (A Fast Parallel Clustering Algorithm for Large Spatial Databases, JOCHEN JAGER, HANS-PETER KRIEGEL)
• (АЛГОРИТМЫ КЛАСТЕРИЗАЦИИ В ЗАДАЧАХ СЕГМЕНТАЦИИ СПУТНИКОВЫХ ИЗОБРАЖЕНИЙ, Пестунов Игорь Алексеевич, Синявский Юрий Николаевич)

2.2.1 Литература

<references \>