Компактная схема метода Гаусса для трёхдиагональной матрицы, последовательный вариант: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Frolov (обсуждение | вклад) |
Frolov (обсуждение | вклад) |
||
| Строка 95: | Строка 95: | ||
=== Описание локальности данных и вычислений === | === Описание локальности данных и вычислений === | ||
=== Возможные способы и особенности реализации параллельного алгоритма === | === Возможные способы и особенности реализации параллельного алгоритма === | ||
| + | |||
| + | Компактная схема метода Гаусса в применении к разложению трёхдиагональной матрицы - это чисто последовательный алгоритм. Его невозможно исполнять параллельно из-за того, что каждая из операций требует в качестве данных результат предыдущей и сама, в свою очередь, отдаёт результат как входное данное для следующей. | ||
| + | |||
| + | Варианты распараллеливания компактной схемы метода Гаусса для трёхдиагональной матрицы используют ассоциативность операций, и, следовательно, представляют собой совсем другие алгоритмы, которые можно изучить на [[Компактная схема метода Гаусса для трёхдиагональной матрицы и её модификации|соответствующей странице]]. | ||
| + | |||
| + | Кроме этого, возможен случай, когда нужны многие разложения трёхдиагональных матриц, тогда этот последовательный алгоритм может быть параллельно выполнен для этих матриц. | ||
| + | |||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
Версия 14:44, 7 июля 2015
| Компактная схема метода Гаусса для трёхдиагональной матрицы | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]3n-3[/math] |
| Объём входных данных | [math]3n-2[/math] |
| Объём выходных данных | [math]3n-2[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]3n-3[/math] |
| Ширина ярусно-параллельной формы | [math]1[/math] |
Основные авторы описания: А.В.Фролов
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Описание схемы реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Описание входных и выходных данных
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритмов
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Описание локальности данных и вычислений
- 2.3 Возможные способы и особенности реализации параллельного алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Компактная схема метода Гаусса для трёхдиагональной матрицы[1][2] вычисляет такое [math]LU[/math]-разложение трёхдиагональной матрицы [math]A[/math] на две двухдиагональные, в котором у нижней двухдиагональной матрицы [math]L[/math] на главной диагонали стоят только единицы. При такой фиксации все элементы разложения становятся строго предопределёнными, с точностью до ошибок округления. Компактная схема даёт естественные формулы нахождения остальных элементов получающихся двухдиагональных матриц. [math]LU[/math]-разложение трёхдиагональной матрицы является частным случаем для компактной схемы метода Гаусса общего вида, однако из-за специфики матрицы характеристики алгоритма кардинально меняются по сравнению с компактной схемой для плотных матриц.
1.2 Математическое описание
Формулы метода следующие:
- [math] u_{11} = a_{11} \\ u_{i i+1} = a_{i i+1}, \quad i \in [1, n-1] \\ l_{i+1 i} = a_{i+1 i} / u_{i i} , \quad i \in [1, n-1] \\ u_{ii} = a_{ii} - l_{i i-1} u_{i-1 i}, \quad i \in [2, n] \\ [/math]
1.3 Вычислительное ядро алгоритма
Как видно из формул, n-1 раз повторяется одна и та же последовательность трёх операций: деление, умножение, вычитание.
1.4 Макроструктура алгоритма
В качестве макровершины можно взять последовательность трёх операций: деление, умножение, вычитание. Эти макровершины выполняются в алгоритме n-1 раз.
1.5 Описание схемы реализации последовательного алгоритма
В схеме учтено, что ряд выходных данных вычислять не нужно - они совпадают с входными. В частности,
- [math] u_{11} = a_{11} \\ u_{i i+1} = a_{i i+1}, \quad i \in [1, n-1]. [/math]
В начале процесса [math]i = 1[/math]
1. Вычисляется [math]l_{i+1 i} = a_{i+1 i} / u_{i i}[/math]
[math]i[/math] увеличивается на 1
2. Вычисляется [math]u_{ii} = a_{ii} - l_{i i-1} u_{i-1 i}[/math]
Если [math]i = n[/math], то конец, иначе возврат к п.1.
1.6 Последовательная сложность алгоритма
Для разложения трёхдиагональной матрицы порядка n компактной схемой метода Гаусса в последовательном варианте требуется:
- [math]n-1[/math] делений,
- [math]n-1[/math] умножений,
- [math]n-1[/math] сложений (вычитаний).
При классификации по последовательной сложности, таким образом, компактная схема метода Гаусса для разложения трёхдиагональной матрицы в последовательном варианте относится к алгоритмам с линейной сложностью.
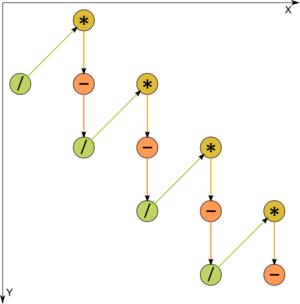
1.7 Информационный граф
1.8 Описание ресурса параллелизма алгоритма
1.9 Описание входных и выходных данных
1.10 Свойства алгоритма
2 Программная реализация алгоритмов
2.1 Особенности реализации последовательного алгоритма
В простейшем варианте алгоритм на Фортране можно записать так:
DO I = 1, N-1
A(I+1,I) = A(I+1,I)/A(I,I)
A(I+1,I+1) = A(I+1,I+1) - A(I+1,I)*A(I,I+1)
END DO
Разложение размещается там же, где размещалась исходная матрица. Однако зачастую трёхдиагональную матрицу, естественно, хранят более экономно. Например, если диагонали нумеруются слева направо и каждая хранится в одной строке массива, то получается такая версия:
DO I = 1, N-1
A(1,I) = A(1,I)/A(2,I)
A(2,I+1) = A(2,I+1) - A(1,I)*A(3,I)
END DO
в которой также разложение хранится на месте исходных данных.
2.2 Описание локальности данных и вычислений
2.3 Возможные способы и особенности реализации параллельного алгоритма
Компактная схема метода Гаусса в применении к разложению трёхдиагональной матрицы - это чисто последовательный алгоритм. Его невозможно исполнять параллельно из-за того, что каждая из операций требует в качестве данных результат предыдущей и сама, в свою очередь, отдаёт результат как входное данное для следующей.
Варианты распараллеливания компактной схемы метода Гаусса для трёхдиагональной матрицы используют ассоциативность операций, и, следовательно, представляют собой совсем другие алгоритмы, которые можно изучить на соответствующей странице.
Кроме этого, возможен случай, когда нужны многие разложения трёхдиагональных матриц, тогда этот последовательный алгоритм может быть параллельно выполнен для этих матриц.