Уровень алгоритма

Участник:Khotkin/Построение матрицы Адамара произвольного размера: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
(Содержимое страницы заменено на «___»)
Строка 1: Строка 1:
−
___
+
еееее
 +
Всем привет! Здесь Кирилл Хоткин и Михаил Царев делают задание по суперкомпьютерам.
 +
{{algorithm
 +
| name              = Сюда тоже запилим
 +
| serial_complexity = <math>O(m2^{2m})</math>
 +
| pf_height        = <math>O(1)</math>
 +
| pf_width          = <math>O(2^{2n})</math>
 +
| input_data        = <math>1</math>
 +
| output_data      = <math>2^{2n}</math>
 +
}}
 +
 
 +
Основные авторы описания: [[Участник:Frolov|А.В.Фролов]], [[Участник:VadimVV|Вад.В.Воеводин]] ([[#Описание локальности данных и вычислений|раздел 2.2]]), [[Участник:Teplov|А.М.Теплов]] (разделы [[#Масштабируемость алгоритма и его реализации|2.4]], [[#Динамические характеристики и эффективность реализации алгоритма|2.5]])
 +
 
 +
== Свойства и структура алгоритма ==
 +
 
 +
=== Общее описание алгоритма ===
 +
 
 +
'''Матрица Адамара''' <math>H</math> порядка <math>n</math> представляет собой матрицу размера  ''n''×''n'' из элементов  <math>+1</math> и <math>-1</math>, такую, что: <math>H \cdot H^T = n \cdot E_n,</math>
 +
где <math>E_n</math> — это единичная матрица размера ''n''×''n''.
 +
 
 +
Матрицы Адамара находят широкое применение в теории кодирования (коды, исправляющие ошибки), теории планирования многофакторных экспериментов (ортогональные блок-схемы), квантовой информатике и прочих областях.
 +
 
 +
Матрица Адамара остаётся матрицей Адамара при следующих преобразованиях:
 +
* умножение строчки или столбца на −1;
 +
* перестановка строчек или столбцов местами.
 +
 
 +
Матрицы Адамара, получаемые друг из друга многократным применением указанных выше преобразований называются эквивалентными.
 +
 
 +
Матрица Адамара называется нормализованной, если её первая строка и столбец состоят только из единиц.
 +
 
 +
Под матрицией Адамара <math>H_m</math> подразумевается матрица порядка <math>2^m</math>
 +
 
 +
Примерами матриц Адамара различных размеров являются следующие матрицы:
 +
 
 +
<math>H_0 = (1);</math>
 +
 
 +
<math>H_1 =
 +
\begin{pmatrix} 1 & 1
 +
\\1 & -1
 +
\end{pmatrix};
 +
</math>
 +
 
 +
<math>H_2 =
 +
\begin{pmatrix} 1 & 1 & 1 & 1
 +
\\1 & -1 & 1 & -1
 +
\\1 & 1 &- 1 & -1
 +
\\1 & -1 & -1 & 1
 +
\end{pmatrix}.
 +
</math>
 +
 
 +
Вообще, если <math>H_m</math> матрица Адамара порядка <math>2^m</math>, то матрица
 +
<math>H_{m+1} =
 +
\begin{pmatrix} H_m & H_m
 +
\\H_m & -H_m
 +
\end{pmatrix}
 +
</math>
 +
является матрицей Адамара порядка <math>2^{m+1}</math>
 +
 
 +
Кроме того, матрицу Адамара порядка <math>2^m</math> можно получить по следующей формуле <math>H^{\otimes m} = H_1  \otimes ... \otimes H_1</math>, где знак <math> \otimes </math> означает тензорное произведение.
 +
 
 +
Также существует недоказанная гипотеза Адамара, которая утверждает, что существуют матрицы Адамара порядка <math>4k</math> для любого натурального <math>k</math>, однако матрица Адамара порядка <math>268</math>  до сих пор не построена, как и для ряда других порядков больше <math>268</math>. Поэтому в данной работе будут рассматриваться матрицы Адамара порядка <math>2^m</math>.
 +
 
 +
=== Математическое описание алгоритма ===
 +
Описанные ранее способы построения матрицы Адамара не являются оптимальными, поэтому вычисление матрицы Адамара порядка <math>2^m</math> будет производится поэлементно с помощью следующей формулы:
 +
 
 +
<math>
 +
(H_m)_{ij}=(-1)^ {\sum_{k}{(i \& j)_k}},
 +
</math>
 +
 
 +
где <math>\& - </math> побитовая операция И,
 +
 
 +
<math>(i \& j)_k - </math> <math>k</math> -ый разряд в двоичном представлении числа <math>(i \& j)</math>.
 +
 
 +
=== Вычислительное ядро алгоритма ===
 +
Вычислительным ядром алгоритма является вычисление элементов матрицы Адамара:
 +
 
 +
<math>
 +
(H_m)_{ij}=(-1)^ {\sum_{k}{(i \& j)_k}}.
 +
</math>
 +
 
 +
=== Макроструктура алгоритма ===
 +
Как и в описании ядра алгоритма, основной частью алгоритма является вычисления очередного элемента матрицы Адамара с помощью следующего выражения:
 +
 
 +
<math>(-1)^ {\sum_{k}{(i \& j)_k}}.</math>
 +
 
 +
=== Схема реализации последовательного алгоритма ===
 +
Для вычисления очередного элемента матрицы Адамара нужно выполнить следующие шаги:
 +
 
 +
1.  Побитовое умножение <math>i</math> и <math>j</math>:  <math>result = i \& j </math> ;
 +
 
 +
2. Нахождение числа единиц в двоичной записи числа <math>result </math>:  <math> sum = \sum_{k}{(result)_k} </math>;
 +
 
 +
3. Нахождение элемента матрицы Адамара: <math>(H_m)_{ij}=(-1)^{sum}</math>.
 +
 
 +
 
 +
Возможная реализация на языке C++:
 +
 
 +
<source lang="C">
 +
 
 +
int get_sign(unsigned N) {
 +
    int i;
 +
    for (i=0; N; N>>=1) { i+=N&1;}
 +
    return (i&1) ? -1 : 1;
 +
}
 +
void adamar(int **e, int size) {
 +
    for (unsigned int i = 0; i < size; ++i)
 +
        for (unsigned int j = 0; j < size; ++j)
 +
            e[i][j]=get_sign(i&j);
 +
}
 +
</source>
 +
 
 +
=== Последовательная сложность алгоритма ===
 +
Для выполнения первого шага алгоритма для всех элементов матрицы Адамара необходимо суммарно выполнить:
 +
* <math>2^{2m}</math> операций побитового умножения.
 +
На втором шаге алгоритма необходимо выполнить для каждого элемента матрицы Адамара:
 +
* от 0 до m или m логических сдвигов на один бит в зависимости от программной реализации;
 +
* от 0 до m или m операций сложения в зависимости от программной реализации;
 +
* от 0 до m или m операций логического умножения в зависимости от программной реализации.
 +
На третьем шаге для всех элементов необходимо сумарно выполнить:
 +
* <math>2^{2m}</math> операций побитового умножения;
 +
* <math>2^{2m}</math> операций сравнения с нулем.
 +
 
 +
 
 +
 
 +
Взяв в расчет не самую лучшую программную реализацию второго шага, всего потребуется выполнение следующего количества операций:
 +
* <math>(m+2)2^{2m}</math> операций логического умножения;
 +
* <math>m\cdot2^{2m}</math> операций сложения;
 +
* <math>m\cdot2^{2m}</math> операций логического сдвига на один бит;
 +
* <math>2^{2m}</math> операций сравнения с нулем.
 +
Всего  <math>(3m+3)2^{2m}</math> операций.
 +
 
 +
=== Информационный граф ===
 +
 
 +
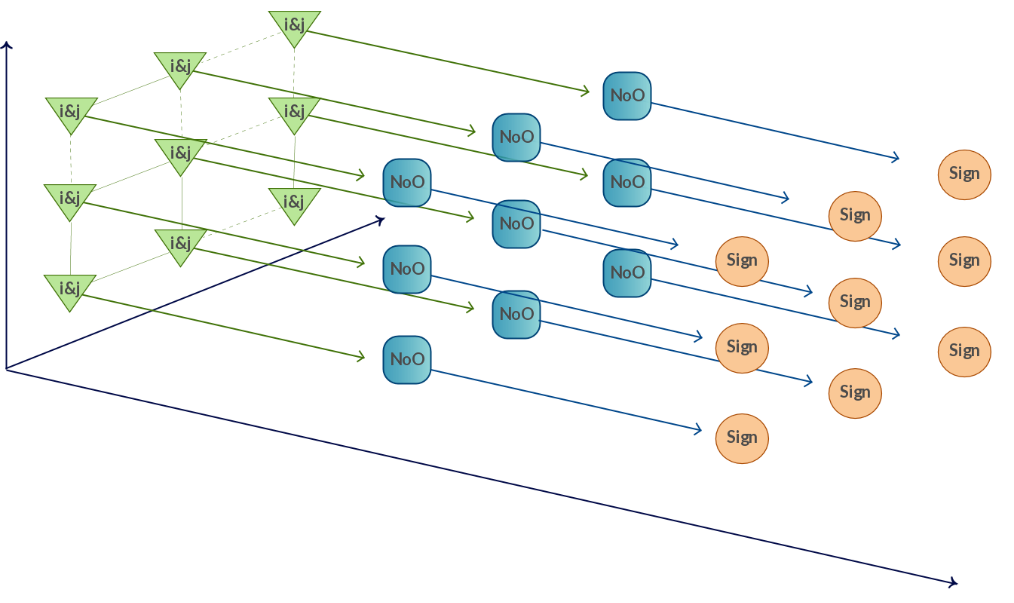
На рисунке ниже изображен информационный граф алгоритма.
 +
 
 +
*<math>i\&j</math> - операция побитового умножения, где <math>i</math> и <math>j</math> соответствующие координаты элемента <math>h_{ij}</math>;
 +
* NoO (number of ones) - вычисление количества единиц числа в двоичной системе. Состоит из последовательного применения операций сложения и побитового умножения;
 +
* Sign - определение знака соответствующего элемента. Если результат предыдущего шага - чётное число, то знак положительный, иначе - отрицательный. 
 +
 
 +
[[File:Hadamar matrix.png|thumb|center|1400px|Рисунок 1. Граф алгоритма построения матрицы Адамара.]]
 +
 
 +
=== Ресурс параллелизма алгоритма ===
 +
Вычисление любого элемента можно производить независимо от других, то есть параллельно.
 +
 
 +
Высота канонической ярусно-параллельной формы равна 3.
 +
Ширина ЯПФ равна <math>2^{2m}</math>.
 +
 
 +
=== Входные и выходные данные алгоритма ===
 +
'''Входные данные''': m - размерность матрицы <math>H_m</math>.
 +
 
 +
'''Объём входных данных''': 1 (число m).
 +
 
 +
'''Выходные данные''': матрица Адамара <math>H_{m}</math> размерностью <math>2^m</math>.
 +
 
 +
'''Объём выходных данных''': <math>2^{2m}</math>.
 +
 
 +
=== Свойства алгоритма ===
 +
* Алгоритм построения матрицы Адамара является ''не детерминированным'', так как число операций меняется в зависимости от входных данных (числа n, которое формирует матрицу размерности 2<sup>''n''</sup>&nbsp;&times;&nbsp;2<sup>''n''</sup>);
 +
* Данный алгоритм построения матрицы Адамара не является ''сбалансированным''. Так как каждый элемент матрицы может обрабатываться независимо от других, вычисление элементов можно распределить по процессам. В случае, когда количество элементов матрицы <math>n</math> не кратно количеству процессов <math>s</math>, на некоторые процессы ложится дополнительная задача вычисления элементов матрицы в количестве <math>a=n\mod s</math>.
 +
 
 +
==Программная реализация алгоритма==
 +
===Особенности реализации последовательного алгоритма===
 +
 
 +
Учитывая, что рассматриваемый алгоритм строит симметричные матрицы Адамара, можно уменьшить количество вычисляемых элементов c <math>2^{2n}</math> до <math>\frac{2^n+2^{2n}}{2}</math> путем вычисления только диагональных и наддиагональных элементов.
 +
 
 +
=== Локальность данных и вычислений ===
 +
=== Возможные способы и особенности параллельной реализации алгоритма ===
 +
=== Масштабируемость алгоритма и его реализации ===
 +
=== Динамические характеристики и эффективность реализации алгоритма ===
 +
=== Выводы для классов архитектур ===
 +
=== Существующие реализации алгоритма ===
 +
== Литература ==

Версия 23:47, 15 октября 2016

еееее Всем привет! Здесь Кирилл Хоткин и Михаил Царев делают задание по суперкомпьютерам.


Сюда тоже запилим
Последовательный алгоритм
Последовательная сложность [math]O(m2^{2m})[/math]
Объём входных данных [math]1[/math]
Объём выходных данных [math]2^{2n}[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]O(1)[/math]
Ширина ярусно-параллельной формы [math]O(2^{2n})[/math]


Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (раздел 2.2), А.М.Теплов (разделы 2.4, 2.5)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Матрица Адамара [math]H[/math] порядка [math]n[/math] представляет собой матрицу размера n×n из элементов [math]+1[/math] и [math]-1[/math], такую, что: [math]H \cdot H^T = n \cdot E_n,[/math] где [math]E_n[/math] — это единичная матрица размера n×n.

Матрицы Адамара находят широкое применение в теории кодирования (коды, исправляющие ошибки), теории планирования многофакторных экспериментов (ортогональные блок-схемы), квантовой информатике и прочих областях.

Матрица Адамара остаётся матрицей Адамара при следующих преобразованиях:

  • умножение строчки или столбца на −1;
  • перестановка строчек или столбцов местами.

Матрицы Адамара, получаемые друг из друга многократным применением указанных выше преобразований называются эквивалентными.

Матрица Адамара называется нормализованной, если её первая строка и столбец состоят только из единиц.

Под матрицией Адамара [math]H_m[/math] подразумевается матрица порядка [math]2^m[/math]

Примерами матриц Адамара различных размеров являются следующие матрицы:

[math]H_0 = (1);[/math]

[math]H_1 = \begin{pmatrix} 1 & 1 \\1 & -1 \end{pmatrix}; [/math]

[math]H_2 = \begin{pmatrix} 1 & 1 & 1 & 1 \\1 & -1 & 1 & -1 \\1 & 1 &- 1 & -1 \\1 & -1 & -1 & 1 \end{pmatrix}. [/math]

Вообще, если [math]H_m[/math] матрица Адамара порядка [math]2^m[/math], то матрица [math]H_{m+1} = \begin{pmatrix} H_m & H_m \\H_m & -H_m \end{pmatrix} [/math] является матрицей Адамара порядка [math]2^{m+1}[/math]

Кроме того, матрицу Адамара порядка [math]2^m[/math] можно получить по следующей формуле [math]H^{\otimes m} = H_1 \otimes ... \otimes H_1[/math], где знак [math] \otimes [/math] означает тензорное произведение.

Также существует недоказанная гипотеза Адамара, которая утверждает, что существуют матрицы Адамара порядка [math]4k[/math] для любого натурального [math]k[/math], однако матрица Адамара порядка [math]268[/math] до сих пор не построена, как и для ряда других порядков больше [math]268[/math]. Поэтому в данной работе будут рассматриваться матрицы Адамара порядка [math]2^m[/math].

1.2 Математическое описание алгоритма

Описанные ранее способы построения матрицы Адамара не являются оптимальными, поэтому вычисление матрицы Адамара порядка [math]2^m[/math] будет производится поэлементно с помощью следующей формулы:

[math] (H_m)_{ij}=(-1)^ {\sum_{k}{(i \& j)_k}}, [/math]

где [math]\& - [/math] побитовая операция И,

[math](i \& j)_k - [/math] [math]k[/math] -ый разряд в двоичном представлении числа [math](i \& j)[/math].

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является вычисление элементов матрицы Адамара:

[math] (H_m)_{ij}=(-1)^ {\sum_{k}{(i \& j)_k}}. [/math]

1.4 Макроструктура алгоритма

Как и в описании ядра алгоритма, основной частью алгоритма является вычисления очередного элемента матрицы Адамара с помощью следующего выражения:

[math](-1)^ {\sum_{k}{(i \& j)_k}}.[/math]

1.5 Схема реализации последовательного алгоритма

Для вычисления очередного элемента матрицы Адамара нужно выполнить следующие шаги:

1. Побитовое умножение [math]i[/math] и [math]j[/math]:  [math]result = i \& j [/math] ;

2. Нахождение числа единиц в двоичной записи числа [math]result [/math]: [math] sum = \sum_{k}{(result)_k} [/math];

3. Нахождение элемента матрицы Адамара: [math](H_m)_{ij}=(-1)^{sum}[/math].


Возможная реализация на языке C++: 

int get_sign(unsigned N) {
    int i;
    for (i=0; N; N>>=1) { i+=N&1;}
    return (i&1) ? -1 : 1;
}
void adamar(int **e, int size) {
    for (unsigned int i = 0; i < size; ++i)
        for (unsigned int j = 0; j < size; ++j)
            e[i][j]=get_sign(i&j);
}

1.6 Последовательная сложность алгоритма

Для выполнения первого шага алгоритма для всех элементов матрицы Адамара необходимо суммарно выполнить:

  • [math]2^{2m}[/math] операций побитового умножения.

На втором шаге алгоритма необходимо выполнить для каждого элемента матрицы Адамара:

  • от 0 до m или m логических сдвигов на один бит в зависимости от программной реализации;
  • от 0 до m или m операций сложения в зависимости от программной реализации;
  • от 0 до m или m операций логического умножения в зависимости от программной реализации.

На третьем шаге для всех элементов необходимо сумарно выполнить:

  • [math]2^{2m}[/math] операций побитового умножения;
  • [math]2^{2m}[/math] операций сравнения с нулем.


Взяв в расчет не самую лучшую программную реализацию второго шага, всего потребуется выполнение следующего количества операций:

  • [math](m+2)2^{2m}[/math] операций логического умножения;
  • [math]m\cdot2^{2m}[/math] операций сложения;
  • [math]m\cdot2^{2m}[/math] операций логического сдвига на один бит;
  • [math]2^{2m}[/math] операций сравнения с нулем.

Всего [math](3m+3)2^{2m}[/math] операций.

1.7 Информационный граф

На рисунке ниже изображен информационный граф алгоритма.

  • [math]i\&j[/math] - операция побитового умножения, где [math]i[/math] и [math]j[/math] соответствующие координаты элемента [math]h_{ij}[/math];
  • NoO (number of ones) - вычисление количества единиц числа в двоичной системе. Состоит из последовательного применения операций сложения и побитового умножения;
  • Sign - определение знака соответствующего элемента. Если результат предыдущего шага - чётное число, то знак положительный, иначе - отрицательный.
Рисунок 1. Граф алгоритма построения матрицы Адамара.

1.8 Ресурс параллелизма алгоритма

Вычисление любого элемента можно производить независимо от других, то есть параллельно.

Высота канонической ярусно-параллельной формы равна 3. Ширина ЯПФ равна [math]2^{2m}[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: m - размерность матрицы [math]H_m[/math].

Объём входных данных: 1 (число m).

Выходные данные: матрица Адамара [math]H_{m}[/math] размерностью [math]2^m[/math].

Объём выходных данных: [math]2^{2m}[/math].

1.10 Свойства алгоритма

  • Алгоритм построения матрицы Адамара является не детерминированным, так как число операций меняется в зависимости от входных данных (числа n, которое формирует матрицу размерности 2n × 2n);
  • Данный алгоритм построения матрицы Адамара не является сбалансированным. Так как каждый элемент матрицы может обрабатываться независимо от других, вычисление элементов можно распределить по процессам. В случае, когда количество элементов матрицы [math]n[/math] не кратно количеству процессов [math]s[/math], на некоторые процессы ложится дополнительная задача вычисления элементов матрицы в количестве [math]a=n\mod s[/math].

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

Учитывая, что рассматриваемый алгоритм строит симметричные матрицы Адамара, можно уменьшить количество вычисляемых элементов c [math]2^{2n}[/math] до [math]\frac{2^n+2^{2n}}{2}[/math] путем вычисления только диагональных и наддиагональных элементов.

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

3 Литература

Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Khotkin/Построение_матрицы_Адамара_произвольного_размера&oldid=11944