Difference between revisions of "The serial-parallel summation method"
| [unchecked revision] | [checked revision] |
| (35 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Primary authors of this description: [[:ru:Участник:Frolov|A.V.Frolov]] | + | {{level-a}} |
| + | |||
| + | Primary authors of this description: [[:ru:Участник:Frolov|A.V.Frolov]]. | ||
== Properties and structure of the algorithm == | == Properties and structure of the algorithm == | ||
| Line 48: | Line 50: | ||
=== Information graph === | === Information graph === | ||
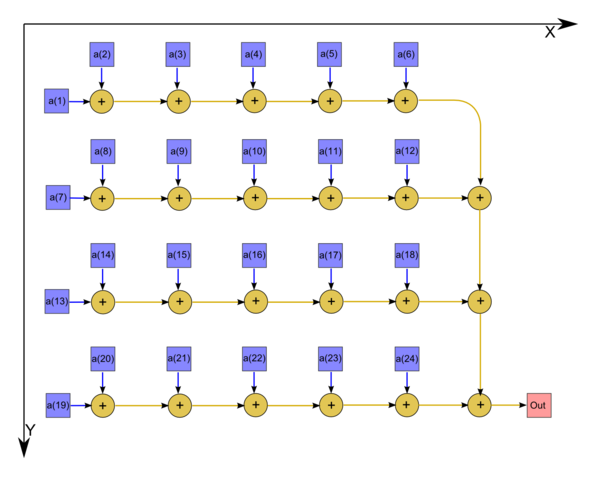
| − | + | The algorithm graph is shown in fig.1 in the case where an array of size 24 is summed. | |
| − | + | [[file:Series-parallel_summation_graph.png|center|thumb|600px|Figure 1. The serial-parallel summation method]] | |
| − | [[file:Series-parallel_summation_graph.png|center|thumb|600px| | ||
<center> | <center> | ||
| Line 60: | Line 61: | ||
}} | }} | ||
<br/> | <br/> | ||
| − | + | Interactive representation of the algorithm graph in the case where an array of size 24 is summed. No input and output data are shown. | |
| − | </center> | + | [[Media:[[Media:Example.ogg]]]] </center> |
=== Parallelization resource of the algorithm === | === Parallelization resource of the algorithm === | ||
| − | + | In order to sum an array of size <math>n</math> by using the serial-parallel summation method in a parallel mode, the following layers must be performed: | |
| − | * <math>k - 1</math> | + | * <math>k - 1</math> layers for the summation of parts of the array (<math>p</math> branches), |
| − | * <math>p - 1</math> | + | * <math>p - 1</math> summation layers (a single serial branch). |
| − | + | Thus, in the parallel version, the critical path of the algorithm (and the corresponding height of the parallel form) depends on the chosen splitting of the array. In the optimal case (<math>p = \sqrt{n}</math>), the height of the parallel form is <math>2 \sqrt{n} - 2</math>. | |
| − | + | Consequently, in terms of the parallel form height, the serial-parallel summation method is qualified as an algorithm of the ''square root'' complexity. In terms of the parallel form width, it also has the ''square root'' complexity. | |
=== Input and output data of the algorithm === | === Input and output data of the algorithm === | ||
| − | + | Input data: array <math>\vec{x}</math> (with elements <math>x_i</math>). | |
| − | + | Further restrictions: none. | |
| − | + | Size of the input data: <nowiki/><math>N</math>. | |
| − | + | Output data: sum of the array's elements. | |
| − | + | Size of the output data: single scalar. | |
=== Properties of the algorithm === | === Properties of the algorithm === | ||
| − | + | It is clearly seen that, in the case of unlimited resources, the ratio of the serial to parallel complexity has the ''square root'' order (the ratio of the linear to square root complexity). The computational power of the algorithm, understood as the ratio of the number of operations to the total size of the input and output data, is only ''1 (the size of the input and output data is equal to the number of operations)''. The algorithm is not completely determined because the partial summations can be organized in different ways. Choosing the order of performing associative operations in accordance with the peculiarities of the input data may reduce the impact of round-off errors at the result. The edges of the information graph are local. | |
== Software implementation of the algorithm == | == Software implementation of the algorithm == | ||
| Line 93: | Line 94: | ||
=== Implementation peculiarities of the serial algorithm === | === Implementation peculiarities of the serial algorithm === | ||
| − | + | The simplest variant (with no order of summation changed) can be written in Fortran as follows: | |
| + | |||
<source lang="fortran"> | <source lang="fortran"> | ||
DO I = 1, P | DO I = 1, P | ||
| Line 113: | Line 115: | ||
</source> | </source> | ||
| − | + | One can also write a similar scheme with the summations performed in the reverse order. We emphasize that, for both schemes, the algorithm graph is [[#Information graph|the same]]! | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Possible methods and considerations for parallel implementation of the algorithm === | === Possible methods and considerations for parallel implementation of the algorithm === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | In its pure form, the serial-parallel method for summation an array is rarely used. Usually, modifications of this method are met in practice. They are designed for calculating the dot product (in which case, products of the elements of two arrays are summed rather than the elements of a single array) or the uniform norm (instead of the elements of an array, their moduli are summed), etc. The method is applied in the BLAS library for calculating the dot product in a particular case (where one of the dimensions is 5); however, the aim apparently was not a parallelization but an optimization of functioning the processor registers. Meanwhile, partitions of an array for calculating partial sums may be useful for better using the cache at individual nodes. | |
| − | === | + | === Run results === |
=== Conclusions for different classes of computer architecture === | === Conclusions for different classes of computer architecture === | ||
| − | |||
| − | + | == References == | |
| − | |||
<references /> | <references /> | ||
| − | [[Category: | + | [[Category:Finished articles]] |
[[Ru:Последовательно-параллельный метод суммирования]] | [[Ru:Последовательно-параллельный метод суммирования]] | ||
Latest revision as of 15:12, 8 July 2022
Primary authors of this description: A.V.Frolov.
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
The serial-parallel method is used as a substitute for the block implementation of calculating long sequences of associative operations (for instance, mass summations). The method became popular due to the following features: a) it realizes the conversion of single cycles into double ones; b) on serial computers and for certain operations, the method was able to reduce the impact of round-off errors at the results. Here, we describe its version for summing numbers.
1.2 Mathematical description of the algorithm
Input data: one-dimensional array of [math]N[/math] numbers.
Output data: sum of the array's elements.
Formulas of the method: the integer [math]N[/math] is represented as [math]N = (p - 1) k + q[/math], where [math]p[/math] is the number of processors, [math]k = \lceil \frac{N}{p} \rceil[/math], and [math]q = N - k (p - 1)[/math].
Then the [math]i[/math]-th processor (where [math]i \lt p[/math]) calculates, in a serial mode, the sum of array elements with the indices ranging from [math](i - 1) k + 1[/math] to [math]i k[/math].
- [math]S_i = \sum_{j = 1}^k x_{k (i - 1) + j}[/math]
The [math]p[/math]-th processor calculates, in a serial mode, the sum of array elements with the indices ranging from [math](p - 1) k + 1[/math] to [math](p - 1) k + q[/math].
- [math]S_p = \sum_{j = 1}^q x_{k (p - 1) + j}[/math]
When this process is completed, the processors exchange their data, and one of them (or each of them if the result is later needed to all the processors) adds the partial sums in a serial mode.
- [math]\sum_{i = 1}^p S_i[/math]
1.3 Computational kernel of the algorithm
The computational kernel of the serial-parallel summation method can be compiled from multiple calculations of partial sums (altogether [math]p[/math] calculations)
- [math]S_i = \sum_{j = 1}^k x_{k (i - 1) + j}[/math]
plus the addition of these partial sums
- [math]\sum_{i = 1}^p S_i[/math]
1.4 Macro structure of the algorithm
As already noted in the description of the computational kernel, the basic part of the method is compiled of multiple calculations (altogether [math]p + 1[/math] calculations) of the sums
- [math]S_i = \sum_{j = 1}^k x_{k (i - 1) + j}[/math] and
- [math]\sum_{i = 1}^p S_i[/math]
1.5 Implementation scheme of the serial algorithm
The formulas of the method are given above. The summations can be performed in different ways, with indices of the summands either increasing or decreasing. When no special reasons for reordering are present, the natural order (i.e., increasing indices) is usually used.
1.6 Serial complexity of the algorithm
Let an array of [math]N[/math] elements must be summed. Various decompositions of [math]N[/math] differ from each other merely by arrangements of parentheses in the summation formula. The number of operations is the same for all the arrangements and is equal to [math]N - 1[/math]. Therefore, in terms of the number of serial operations, the method should be regarded as a linear complexity algorithm.
1.7 Information graph
The algorithm graph is shown in fig.1 in the case where an array of size 24 is summed.
Interactive representation of the algorithm graph in the case where an array of size 24 is summed. No input and output data are shown.
1.8 Parallelization resource of the algorithm
In order to sum an array of size [math]n[/math] by using the serial-parallel summation method in a parallel mode, the following layers must be performed:
- [math]k - 1[/math] layers for the summation of parts of the array ([math]p[/math] branches),
- [math]p - 1[/math] summation layers (a single serial branch).
Thus, in the parallel version, the critical path of the algorithm (and the corresponding height of the parallel form) depends on the chosen splitting of the array. In the optimal case ([math]p = \sqrt{n}[/math]), the height of the parallel form is [math]2 \sqrt{n} - 2[/math].
Consequently, in terms of the parallel form height, the serial-parallel summation method is qualified as an algorithm of the square root complexity. In terms of the parallel form width, it also has the square root complexity.
1.9 Input and output data of the algorithm
Input data: array [math]\vec{x}[/math] (with elements [math]x_i[/math]).
Further restrictions: none.
Size of the input data: [math]N[/math].
Output data: sum of the array's elements.
Size of the output data: single scalar.
1.10 Properties of the algorithm
It is clearly seen that, in the case of unlimited resources, the ratio of the serial to parallel complexity has the square root order (the ratio of the linear to square root complexity). The computational power of the algorithm, understood as the ratio of the number of operations to the total size of the input and output data, is only 1 (the size of the input and output data is equal to the number of operations). The algorithm is not completely determined because the partial summations can be organized in different ways. Choosing the order of performing associative operations in accordance with the peculiarities of the input data may reduce the impact of round-off errors at the result. The edges of the information graph are local.
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
The simplest variant (with no order of summation changed) can be written in Fortran as follows:
DO I = 1, P
S (I) = X(K*(I-1)+1)
IF (I.LQ.P) THEN
DO J = 2,K
S(I)=S(I)+X(K*(I-1)+J)
END DO
ELSE
DO J = 2,Q
S(I)=S(I)+X(K*(I-1)+J)
END DO
END IF
END DO
SUM = S(1)
DO I = 2, P
SUM = SUM + S(I)
END DO
One can also write a similar scheme with the summations performed in the reverse order. We emphasize that, for both schemes, the algorithm graph is the same!
2.2 Possible methods and considerations for parallel implementation of the algorithm
In its pure form, the serial-parallel method for summation an array is rarely used. Usually, modifications of this method are met in practice. They are designed for calculating the dot product (in which case, products of the elements of two arrays are summed rather than the elements of a single array) or the uniform norm (instead of the elements of an array, their moduli are summed), etc. The method is applied in the BLAS library for calculating the dot product in a particular case (where one of the dimensions is 5); however, the aim apparently was not a parallelization but an optimization of functioning the processor registers. Meanwhile, partitions of an array for calculating partial sums may be useful for better using the cache at individual nodes.