Algorithm level

Difference between revisions of "Purdom's algorithm"

From Algowiki
Jump to navigation Jump to search
[unchecked revision][unchecked revision]
Line 32: Line 32:
 
# Breadth-first searches in the intermediate representation resulting in the final transitive closure.  
 
# Breadth-first searches in the intermediate representation resulting in the final transitive closure.  
  
−
1. В случае решения задачи проверки принадлежности к транзитивному замыканию множество заданных пар вершин, соотношение объемов различных вычислительных частей алгоритма может быть очень различным, и, очевидно, зависит от числа пар входных вершин. Кроме того, данное соотношение может так же зависеть от типа входного графа, так как структура и количество сильно-связанных компонент сильно влияют как на время поиска сильно-связанных компонент, так и на время выполнения поисков в ширину. Далее представлена таблица, демонстрирующая процент времени выполнения данных частей для одной из реализаций алгоритма для различных типов графов с числом вершин <math>2^{23}</math>, и числом входных пар вершин для проверки равным 10000.
+
1. Suppose that the algorithm should verify whether node pairs in the given set belong to the transitive closure. In this case, the relative weight of an individual computational stage may vary widely. It obviously depends on the number of input node pairs. Besides, it may depend on the type of the input graph because the structure and the number of strongly connected components affect strongly both the time for finding these components and the time for performing breadth-first searches. The table below demonstrates (for a certain implementation of Purdom's algorithm) the percentage of the total execution time spent on the individual stages. Various types of graph were examined. The number of nodes was
 +
<math>2^{23}</math>, and the number of input node pairs was 10000.
  
−
[[file:Purdom_time_table.png|thumb|center|500px|Рисунок 1. Сравнение времни выполнения различных частей алгоритма Пурдома одной из реализаций..]]
+
[[file:Purdom_time_table.png|thumb|center|500px|Figure 1. Comparison of execution times of the individual stages for a certain implementation of Purdom's algorithm]]
  
−
Важно заметить, что некоторые алгоритмы поиска сильно-связанных компонент (например DCSC) так же основываются на поиска в ширину. Таким образом, вычислительным ядром алгоритма можно считать поиск в ширину. В свою очередь вычислительным ядром алгоритма поиска в ширину является обход вершин, смежной к выбранной вершине с последующем добавлением еще не посещенных вершин в множество "передовых" вершин.  
+
It is important to notice that some algorithms for finding strongly connected components (for instance, the DSCS algorithm) are also based on breadth-first searches. Thus, breadth-first searches can be regarded as the computational kernel of the algorithm. The computational kernel of the breadth-first search is, in turn, the traversal of neighbor nodes for a singled-out node and the addition of not yet visited nodes to the set of "advanced" nodes.
  
−
2. В случае решения задачи поиска полного транзитивного замыкания наиболее вычислительно затратной частью являются поиски в ширину в графе промежуточного представления, так как его необходимо произвести от всех вершин данного графа, число которых может быть значительным при большом числе сильно-связанных компонент в исходном графе.
+
2. Now, suppose that the complete transitive closure is sought. Then the computationally most laborious stage are breadth-first searches in the intermediate representation  так как его необходимо произвести от всех вершин данного графа, число которых может быть значительным при большом числе сильно-связанных компонент в исходном графе.
  
 
=== Macro structure of the algorithm ===
 
=== Macro structure of the algorithm ===

Revision as of 11:13, 18 November 2017


Алгоритм Пурдома
Sequential algorithm
Serial complexity [math]O(|E| + \mu^2)[/math]
Input data [math]O(|E| + |V|)[/math]
Output data [math]O(|V|^2)[/math]
Parallel algorithm
Parallel form height [math]N/A [/math]
Parallel form width [math]N/A[/math]


Primary author of this description: I.V.Afanasyev.

1 Properties and structure of the algorithm

1.1 General description of the algorithm

Purdom's algorithm[1] finds the transitive closure of a directed graph in time [math]O(|E| + \mu |V|)[/math], where [math]\mu \le |E|[/math] is the number of strongly connected components of this graph. The algorithm can be modified to verify whether node pairs in the given set belong to the transitive closure.

1.2 Mathematical description of the algorithm

Purdom's algorithm is based on the following considerations:

  1. If nodes [math]v[/math] and [math]w[/math] belong to the same strongly connected component of the graph [math]G[/math], then its transitive closure [math]G^+[/math] contains the arcs [math](v, w)[/math] and [math](w, v)[/math].
  2. If nodes [math]x[/math] and [math]y[/math] belong to the same strongly connected component of the graph [math]G[/math] and the same is true of nodes [math]z[/math] and [math]t[/math] , then the arcs [math](x, z)[/math], [math](x, t)[/math], [math](y, z)[/math], and [math](y, t)[/math] simultaneously either belong or not belong to the transitive closure.

Thus, the search for the transitive closure of the graph [math]G[/math] reduces to finding the transitive closure of the acyclic graph [math]\tilde G[/math] obtained by merging each strongly connected component of [math]G[/math] into a single node. The transitive closure of an acyclic graph is calculated with the use of the topological sort of its nodes.

1.3 Computational kernel of the algorithm

The algorithm consists of three important computational stages. It is essential to assess the relative execution time of each stage. The stages are:

  1. Search for the strongly connected components in the original graph.
  2. Creating intermediate representation.
  3. Breadth-first searches in the intermediate representation resulting in the final transitive closure.

1. Suppose that the algorithm should verify whether node pairs in the given set belong to the transitive closure. In this case, the relative weight of an individual computational stage may vary widely. It obviously depends on the number of input node pairs. Besides, it may depend on the type of the input graph because the structure and the number of strongly connected components affect strongly both the time for finding these components and the time for performing breadth-first searches. The table below demonstrates (for a certain implementation of Purdom's algorithm) the percentage of the total execution time spent on the individual stages. Various types of graph were examined. The number of nodes was [math]2^{23}[/math], and the number of input node pairs was 10000.

Figure 1. Comparison of execution times of the individual stages for a certain implementation of Purdom's algorithm

It is important to notice that some algorithms for finding strongly connected components (for instance, the DSCS algorithm) are also based on breadth-first searches. Thus, breadth-first searches can be regarded as the computational kernel of the algorithm. The computational kernel of the breadth-first search is, in turn, the traversal of neighbor nodes for a singled-out node and the addition of not yet visited nodes to the set of "advanced" nodes.

2. Now, suppose that the complete transitive closure is sought. Then the computationally most laborious stage are breadth-first searches in the intermediate representation так как его необходимо произвести от всех вершин данного графа, число которых может быть значительным при большом числе сильно-связанных компонент в исходном графе.

1.4 Macro structure of the algorithm

Вычисления производятся в четыре этапа:

  1. Найти компоненты сильной связности исходного графа, заменить каждую компоненту на одну вершину и удалить образовавшиеся рёбра-петли.
  2. Выполнить топологическую сортировку полученного ациклического графа [math]\tilde G[/math].
  3. Вычислить транзитивное замыкание графа [math]\tilde G[/math], двигаясь от вершин с бо́льшими номерами к меньшим.
  4. По найденному транзитивному замыканию [math]\tilde G[/math] восстановить транзитивное замыкание исходного графа.

Последний этап не является обязательным, если рассматривать транзитивное замыкание [math]\tilde G[/math] как «упакованное» транзитивное замыкание [math]G[/math].

1.5 Implementation scheme of the serial algorithm

1 этап (вычисление компонент сильной связности) может быть реализован алгоритмом Тарьяна[2], находящим компоненты сильной связности в ходе поиска в глубину.

2 этап (топологическая сортировка) может быть реализован алгоритмом Кана[3] либо последовательным применением поиска в глубину[2] для нумерации вершин в предпорядке.

3 этап (транзитивное замыкание [math]\tilde G[/math]) выполняется следующим алгоритмом: 

Входные данные:
    ациклический граф 'G с вершинами 'V, пронумерованными в топологическом порядке, и рёбрами E.
Выходные данные:
    для каждой вершины v ∈ V – набор вершин T(v),
        так что транзитивное замыкание G состоит из рёбер (v, w), v ∈ V, w ∈ T(v).
    
for each v ∈ V do T(v) := { v }
for v ∈ V in reverse order:
    for each (v, w) ∈ E do T(v) := T(v) ∪ T(w)

4 этап (транзитивное замыкание [math]G[/math]) либо выполняется следующим алгоритмом: 

Входные данные
    граф G с вершинами V;
    компоненты сильной связности SCC(v) графа G;
    граф [math]\tilde G[/math] с вершинами [math]\tilde V[/math];
    транзитивное замыкание [math]\tilde T[/math] графа [math]\tilde G[/math].
Выходные данные:
    для каждой вершины v ∈ V – набор вершин T(v),
        так что транзитивное замыкание G состоит из рёбер (v, w), v ∈ V, w ∈ T(v).
        
for each v ∈ V do T(v) := { v }
for each v ∈ [math]\tilde V[/math]:
    for each w ∈ [math]\tilde T(v)[/math]:
        T(v) := T(v) ∪ SCC(w)
    for each x ∈ SCC(v):
        T(x) := T(v)    /* присваивание по ссылке */

либо транзитивное замыкание может строиться по упакованным данным [math]\tilde T(v)[/math] одной из следующих функций: 

Входные данные
    граф G с вершинами V;
    компоненты сильной связности SCC(v) графа G;
    отображение R(v) вершин графа G на вершины графа [math]\tilde G[/math];
    граф [math]\tilde G[/math] с вершинами [math]\tilde V[/math];
    транзитивное замыкание [math]\tilde T[/math] графа [math]\tilde G[/math].
    
function transitive_closure(v):
    T := { v }
    for each w ∈ [math]\tilde T(R(v))[/math]:
        T := T ∪ SCC(w)
    return T
    
function is_in_transitive_closure(v, w):
    return R(w) ∈ [math]\tilde T(R(v))[/math]

1.6 Serial complexity of the algorithm

Первый и второй этап выполняются с помощью поиска в глубину со сложностью [math]O(|E|)[/math].

На третьем этапе основой операцией является объединение списков вершин. В случае хранения списков в отсортированном виде объединение выполняется за линейное время. Количество списков не превосходит [math]|V|[/math], а в каждом списке не более [math]\mu[/math] вершин, где [math]\mu[/math] – количество компонент сильной связности. Общая сложность тогда составляет [math]O(\mu^2)[/math]. Альтернативным форматов хранения списка вершин является битовая маска с такой же общей сложностью.

Сложность четвёртого этапа составляет [math]O(\mu |V|)[/math], так как для каждой из [math]\mu[/math] компонент сильной связности за линейное время вычисляется список вершин из не более чем [math]|V|[/math] вершин. Поскольку компоненты сильной связности не пересекаются, на данном этапе уже не требуется хранить списки в отсортированном виде.

Таким образом, общая сложность составляет [math]O(|E| + \mu^2)[/math], если не требуется явное построение транзитивного замыкания, или [math]O(|E| + \mu |V|)[/math] в противном случае.

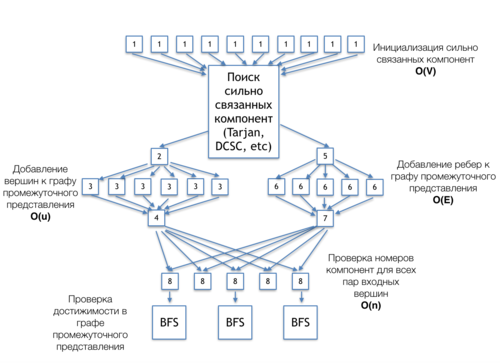
1.7 Information graph

На рисунке 2 представлен информационный граф алгоритма Пурдома, демонстрирующий связь между его основным частями. Алгоритм представлен для вариации постановки задачи, когда производится проверка принадлежности к транзитивному замыканию множества заранее заданных пар вершин.

Рисунок 2. Информационный граф алгоритма Пурдома.

[1] - инициализация массива номеров сильно связанных компонент

[Поиск сильно связанных компонент (Tarjan, DCSC, etc)] - независимый блок алгоритма, может быть реализован любым алгоритмом сильно связанных компонент: DCSC, Тарьяна и др. Информационный графы данных алгоритмов могут быть найдены в соответствующих разделах.

[2] - выделение памяти под вершины графа промежуточного представления

[3] - добавление вершин к графу промежуточного представления, каждая вершина соответствует одной сильно-связанной компоненте

[4] - подсчет числа вершин в графе промежуточного представления

[5] - выделение памяти под ребра графа промежуточного представления

[6] - добавление ребер к графу промежуточного представления, связывающих различные сильно связанные компоненты

[7] - подсчет числа ребер в графе промежуточного представления

[8] - проверка номеров сильно связанных компонент для каждой пары сильно связанных компонент

[BFS] - поиски в ширину от тех вершин, которые находятся в одних сильно связанных компонентах

1.8 Parallelization resource of the algorithm

В данном разделе будет описан ресурс параллелизма, основываясь на информационном графе алгоритма, приведенном на рисунке 2.

Инициализация сильно связанных компонент [1] может производиться параллельно и требует [math]|V|[/math] операций.

Поиск сильно связанных компонент может иметь различный ресурс параллелизма, в зависимости от выбора алгоритма.

Добавление вершин и ребер к графу промежуточного представления [2]-[7] требует [math]|E|[/math] и [math]|u|[/math] операций ([math]u[/math] - число сильно связанных компонент исходного графа), которые так же могут выполняться параллельно. При этом, вершины и ребра добавляются к графу независимо друг от друга, поэтому добавление вершин может производиться параллельно с добавлением ребер.

Проверка номеров сильно связанных компонент [8] так же может выполняться параллельно и требует [math]|n|[/math] операций ([math]n[/math] - число пар вершин, подаваемых на выход), которые так же могут выполняться параллельно.

В случае принаделжности вершин одной пары к одной сильно связанный компоненте, производится поиск в ширину [BFS], для каждой соответствующей пары. Данные поиски в ширину так же могут выполняться параллельно друг другу, при том каждый поиск в ширину имеет определенный ресурс параллелизма, описанный в соответствующем разделе.

Высота и ширина ярусно-параллельной формы зависит от структуры графа (числа и расположения сильно-связанных компонент), так как в свою очередь от нее зависит ширина и высота ЯПФ алгоритма поиска сильно-связанных компонент.

1.9 Input and output data of the algorithm

Объем входных и выходных данных зависит от вариации постановки проблемы. Далее будут рассмотрены два случая.

1. Поиск полного транзитивного замыкания

Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math].

Объём входных данных: [math]O(|V| + |E|)[/math].

Выходные данные: для каждой пары вершин графа её принадлежность к транзитивному замыканию.

Объём выходных данных: [math]O(|V|^2)[/math].

2. Проверка принадлежности к транзитивному замыканию для [math]n[/math] заранее заданных пар вершин [math](v_{i}, v_{j})[/math]

Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math], [math]n[/math] пар вершин [math](v_{i}, v_{j})[/math].

Объём входных данных: [math]O(|V| + |E| + n)[/math].

Выходные данные: для каждой входной пары вершин её принадлежность к транзитивному замыканию.

Объём выходных данных: [math]O(n)[/math].

1.10 Properties of the algorithm

2 Software implementation of the algorithm

2.1 Implementation peculiarities of the serial algorithm

2.2 Locality of data and computations

2.2.1 Locality of implementation

2.2.1.1 Structure of memory access and a qualitative estimation of locality
2.2.1.2 Quantitative estimation of locality

2.3 Possible methods and considerations for parallel implementation of the algorithm

Программа, реализующая поиск транзитного замыкания, состоит CPU части, отвечающей за общую координацию вычислений, использующей вспомогательные классы.

2.4 Scalability of the algorithm and its implementations

2.4.1 Scalability of the algorithm

2.4.2 Scalability of of the algorithm implementation

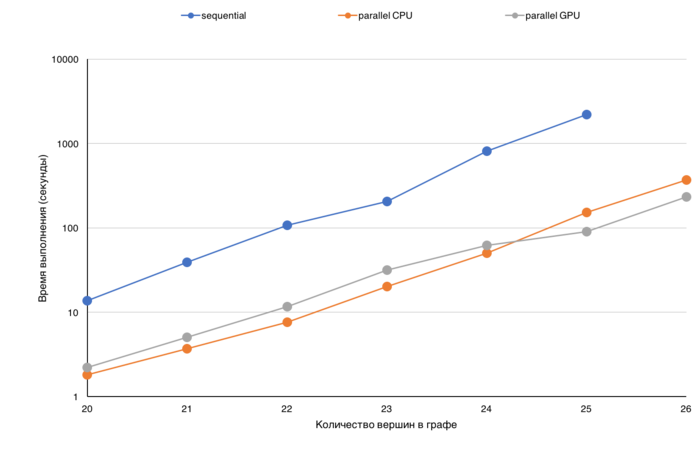
Для демонстрации эффективности представлены графики времени выполнения различных режимов вычислений в зависимости от размера входного графа.

Основной характеристикой для сравнения было выбрано время выполнения, так как производительность (определения как TEPS то есть число ребер графа, которое алгоритм обрабатывает в секунду) для данной операции не отражает реальной ситуации.

Дело в том, что сложность выбранного алгоритма Пурдома зависит от количества ребер в графе не линейно, и, кроме того, зависит еще и от структуры графа количества сильно связанных компонент).

Рисунок 2. Параллельная реализация алгоритма Пурдома масштабируемость различных версий: производительность в зависимости от размера графа.

Анализируя время выполнения можно оценить, насколько понижается эффективность обработки графа при увеличении его размера (данные перестают помещаться в кэш, в память GPU, узла и т.д.). На представленных графиках по оси X граф с каждым делением увеличивается в два раза, и по представленному графику можно оценивать, на сколько увеличилось время выполнения. Так же время выполнения можно сравнивать для различных версий, например, последовательной CPU, параллельной CPU или же GPU. На приведенной диаграмме (рисунок 1) для различных размеров графа (от 2^20 до 2^26) представлено время выполнения трех различных версий: последовательной, параллельной CPU и GPU. Шкала на данной диаграмме логарифмическая.

2.5 Dynamic characteristics and efficiency of the algorithm implementation

2.6 Conclusions for different classes of computer architecture

2.7 Existing implementations of the algorithm

3 References

  1. ↑ Purdom, Paul, Jr. “A Transitive Closure Algorithm.” Bit 10, no. 1 (March 1970): 76–94. doi:10.1007/BF01940892.
  2. ↑ 2.0 2.1 Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.
  3. ↑ Kahn, A B. “Topological Sorting of Large Networks.” Communications of the ACM 5, no. 11 (November 1962): 558–62. doi:10.1145/368996.369025.
Retrieved from "https://algowiki-project.org/algowiki/en/index.php?title=Purdom%27s_algorithm&oldid=1078"