Purdom's algorithm
| Алгоритм Пурдома | |
| Sequential algorithm | |
| Serial complexity | [math]O(|E| + \mu^2)[/math] |
| Input data | [math]O(|E| + |V|)[/math] |
| Output data | [math]O(|V|^2)[/math] |
| Parallel algorithm | |
| Parallel form height | [math]N/A [/math] |
| Parallel form width | [math]N/A[/math] |
Primary author of this description: I.V.Afanasyev.
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 2.1 Implementation peculiarities of the serial algorithm
- 2.2 Locality of data and computations
- 2.3 Possible methods and considerations for parallel implementation of the algorithm
- 2.4 Scalability of the algorithm and its implementations
- 2.5 Dynamic characteristics and efficiency of the algorithm implementation
- 2.6 Conclusions for different classes of computer architecture
- 2.7 Existing implementations of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
Purdom's algorithm[1] finds the transitive closure of a directed graph in time [math]O(|E| + \mu |V|)[/math], where [math]\mu \le |E|[/math] is the number of strongly connected components of this graph. The algorithm can be modified to verify whether node pairs in the given set belong to the transitive closure.
1.2 Mathematical description of the algorithm
Purdom's algorithm is based on the following considerations:
- If nodes [math]v[/math] and [math]w[/math] belong to the same strongly connected component of the graph [math]G[/math], then its transitive closure [math]G^+[/math] contains the arcs [math](v, w)[/math] and [math](w, v)[/math].
- If nodes [math]x[/math] and [math]y[/math] belong to the same strongly connected component of the graph [math]G[/math] and the same is true of nodes [math]z[/math] and [math]t[/math] , then the arcs [math](x, z)[/math], [math](x, t)[/math], [math](y, z)[/math], and [math](y, t)[/math] simultaneously either belong or not belong to the transitive closure.
Thus, the search for the transitive closure of the graph [math]G[/math] reduces to finding the transitive closure of the acyclic graph [math]\tilde G[/math] obtained by merging each strongly connected component of [math]G[/math] into a single node. The transitive closure of an acyclic graph is calculated with the use of the topological sort of its nodes.
1.3 Computational kernel of the algorithm
The algorithm consists of three important computational stages. It is essential to assess the relative execution time of each stage. The stages are:
- Search for the strongly connected components in the original graph.
- Creating intermediate representation.
- Breadth-first searches in the intermediate representation resulting in the final transitive closure.
1. Suppose that the algorithm should verify whether node pairs in the given set belong to the transitive closure. In this case, the relative weight of an individual computational stage may vary widely. It obviously depends on the number of input node pairs. Besides, it may depend on the type of the input graph because the structure and the number of strongly connected components affect strongly both the time for finding these components and the time for performing breadth-first searches. The table below demonstrates (for a certain implementation of Purdom's algorithm) the percentage of the total execution time spent on the individual stages. Various types of graph were examined. The number of nodes was [math]2^{23}[/math], and the number of input node pairs was 10000.
It is important to notice that some algorithms for finding strongly connected components (for instance, the DSCS algorithm) are also based on breadth-first searches. Thus, breadth-first searches can be regarded as the computational kernel of the algorithm. The computational kernel of the breadth-first search is, in turn, the traversal of neighbor nodes for a singled-out node and the addition of not yet visited nodes to the set of "advanced" nodes.
2. Now, suppose that the full transitive closure is sought. Then the computationally most laborious stage are breadth-first searches in the intermediate representation так как его необходимо произвести от всех вершин данного графа, число которых может быть значительным при большом числе сильно-связанных компонент в исходном графе.
1.4 Macro structure of the algorithm
There are four stages in the computation:
- Find the strongly connected components of the original graph, replace each component by a single node, and remove the resulting loops.
- Perform the topological sort of the acyclic graph [math]\tilde G[/math] obtained at stage 1.
- Calculate the transitive closure of [math]\tilde G[/math], moving from nodes with larger indices to those with smaller ones.
- Reconstruct the transitive closure of the original graph from the transitive closure of [math]\tilde G[/math].
The last stage is not required if the transitive closure of [math]\tilde G[/math] is regarded as a "packed" transitive closure of [math]G[/math].
1.5 Implementation scheme of the serial algorithm
Stage 1 (calculation of strongly connected components) can be implemented by using Tarjan's algorithm[2]. This algorithm finds strongly connected components in the course of the depth-first search.
Stage 2 (topological sort) can be implemented either by Kahn's algorithm [3] or by successively using the depth-first search[2] for a preorder numbering of nodes.
Stage 3 (transitive closure of [math]\tilde G[/math]) is performed by the following algorithm:
Input data:
acyclic graph G with nodes V, indexed in the topological order, and arcs E.
Output data:
collection of nodes T(v) for each node v ∈ V; thus, the transitive closure of G consists of arcs (v, w), v ∈ V, w ∈ T(v).
for each v ∈ V do T(v) := { v }
for v ∈ V in reverse order:
for each (v, w) ∈ E do T(v) := T(v) ∪ T(w)
Stage 4 (transitive closure of [math]G[/math]) is performed by the following algorithm:
Input data
graph G with nodes V;
strongly connected components SCC(v) of G;
graph [math]\tilde G[/math] with nodes [math]\tilde V[/math];
transitive closure [math]\tilde T[/math] of [math]\tilde G[/math].
Output data:
collection of nodes T(v) for each node v ∈ V; thus, the transitive closure of G consists of arcs (v, w), v ∈ V, w ∈ T(v).
for each v ∈ V do T(v) := { v }
for each v ∈ [math]\tilde V[/math]:
for each w ∈ [math]\tilde T(v)[/math]:
T(v) := T(v) ∪ SCC(w)
for each x ∈ SCC(v):
T(x) := T(v) /* assignment by reference */
Or one of the following functions can be used for constructing the transitive closure from the packed data [math]\tilde T(v)[/math]:
Input data
graph G with nodes V;
strongly connected components SCC(v) графа G;
mapping R(v) of the nodes of G on the nodes of [math]\tilde G[/math]; graph [math]\tilde G[/math] with nodes [math]\tilde V[/math];
transitive closure [math]\tilde T[/math] of [math]\tilde G[/math].
function transitive_closure(v):
T := { v }
for each w ∈ [math]\tilde T(R(v))[/math]:
T := T ∪ SCC(w)
return T
function is_in_transitive_closure(v, w):
return R(w) ∈ [math]\tilde T(R(v))[/math]
1.6 Serial complexity of the algorithm
The first two stages are performed with the use of depth-first search and have the complexity [math]O(|E|)[/math].
The basic operation of the third stage is the merging of node lists. If these lists are stored in a sorted form, their merging is executed in linear time. The number of lists does not exceed [math]|V|[/math], and each list contains at most [math]\mu[/math] nodes, where [math]\mu[/math] is the number of strongly connected components. Then the overall complexity is [math]O(\mu^2)[/math]. An alternative format for storing node lists is a bit mask; the overall complexity remains the same.
The complexity of the fourth stage is [math]O(\mu |V|)[/math]. Indeed, for each of the [math]\mu[/math] strongly connected components, one calculates its list of nodes in linear time, and each list contains at most [math]|V|[/math] nodes. Since the strongly connected components are disjoint, it is not necessary at this stage to store lists in a sorted form.
Thus, the overall complexity is [math]O(|E| + \mu^2)[/math] if the explicit construction of the transitive closure is not required and [math]O(|E| + \mu |V|)[/math], otherwise.
1.7 Information graph
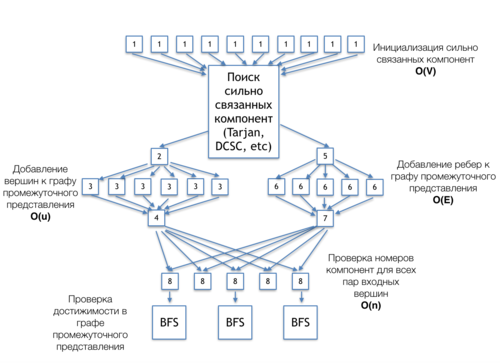
The information graph of Purdom's algorithm shown in figure 2 demonstrates connections between the basic parts of the algorithm. This version corresponds to the case where the algorithm should verify whether node pairs in the given set belong to the transitive closure.
[1] - initialization of the array for storing the indices of strongly connected components.
[The search for strongly connected components (Tarjan, DCSC, etc)] is an independent block of this algorithm. It can be realized by any algorithm for finding strongly connected components: DCSC, Tarjan etc. The information graphs of these algorithms can be found in the corresponding sections.]
[2] - memory allocation for the nodes of the intermediate representation.
[3] - addition of nodes to the intermediate representation. Each node corresponds to a single strongly connected component.
[4] - calculation the number of nodes in the intermediate representation.
[5] - memory allocation for the arcs of the intermediate representation.
[6] - addition of arcs connecting different strongly connected components to the intermediate representation.
[7] - calculation the number of arcs in the intermediate representation.
[8] - test of the indices for each pair of strongly connected components.
[BFS] - breadth-first searches within the same strongly connected component.
1.8 Parallelization resource of the algorithm
In this section, we discuss the parallelization resource of Purdom's algorithm using its information graph shown in figure 2.
The initialization of strongly connected components [1] can be done in parallel and requires [math]|V|[/math] operations.
The parallelization resource of the search for strongly connected components can vary and depends on the choice of algorithm.
The addition of nodes and arcs to the intermediate representation [2]-[7] requires [math]|E|[/math] and [math]|u|[/math] operations (where [math]u[/math] is the number of strongly connected components in the original graph), which can be executed in parallel. Moreover, nodes and arcs are added to the graph independently from each other; consequently, the addition of nodes can be performed in parallel with the addition of arcs.
Tests for the indices of strongly connected components [8] can also be done in parallel. They require [math]|n|[/math] operations (where [math]n[/math] is the number of output node pairs), which can also be executed in parallel.
If both nodes of a pair belong to the same strongly connected component, then a breadth-first search [BFS] is performed. These searches for different pairs can also be done in parallel. The parallelization resource of the breadth-first search is described in the corresponding section.
The height and width of the parallel form depend on the structure of graph (that is, on the number and location of strongly connected components) because this structure affects the height and width of the parallel form of algorithms for finding strongly connected components.
1.9 Input and output data of the algorithm
The size of input and output data depends on the variant of the problem to be solved. Below, we consider two cases.
1. Search for the full transitive closure
Input data: graph [math]G(V, E)[/math] with [math]|V|[/math] nodes [math]v_i[/math] and [math]|E|[/math] arcs [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math].
Size of the input data: [math]O(|V| + |E|)[/math].
Output data: indicate for each pair of graph nodes whether they belong to the transitive closure.
Size of the output data: [math]O(|V|^2)[/math].
2. Проверка принадлежности к транзитивному замыканию для [math]n[/math] заранее заданных пар вершин [math](v_{i}, v_{j})[/math]
Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math], [math]n[/math] пар вершин [math](v_{i}, v_{j})[/math].
Объём входных данных: [math]O(|V| + |E| + n)[/math].
Выходные данные: для каждой входной пары вершин её принадлежность к транзитивному замыканию.
Объём выходных данных: [math]O(n)[/math].
1.10 Properties of the algorithm
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
2.2 Locality of data and computations
2.2.1 Locality of implementation
2.2.1.1 Structure of memory access and a qualitative estimation of locality
2.2.1.2 Quantitative estimation of locality
2.3 Possible methods and considerations for parallel implementation of the algorithm
Программа, реализующая поиск транзитного замыкания, состоит CPU части, отвечающей за общую координацию вычислений, использующей вспомогательные классы.
2.4 Scalability of the algorithm and its implementations
2.4.1 Scalability of the algorithm
2.4.2 Scalability of of the algorithm implementation
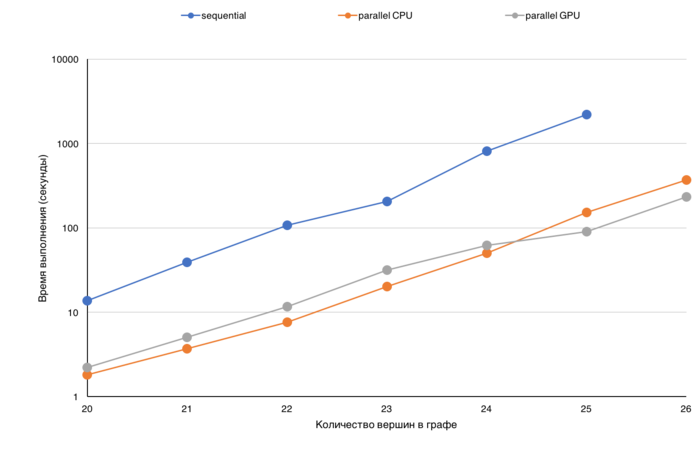
Для демонстрации эффективности представлены графики времени выполнения различных режимов вычислений в зависимости от размера входного графа.
Основной характеристикой для сравнения было выбрано время выполнения, так как производительность (определения как TEPS то есть число ребер графа, которое алгоритм обрабатывает в секунду) для данной операции не отражает реальной ситуации.
Дело в том, что сложность выбранного алгоритма Пурдома зависит от количества ребер в графе не линейно, и, кроме того, зависит еще и от структуры графа количества сильно связанных компонент).
Анализируя время выполнения можно оценить, насколько понижается эффективность обработки графа при увеличении его размера (данные перестают помещаться в кэш, в память GPU, узла и т.д.). На представленных графиках по оси X граф с каждым делением увеличивается в два раза, и по представленному графику можно оценивать, на сколько увеличилось время выполнения. Так же время выполнения можно сравнивать для различных версий, например, последовательной CPU, параллельной CPU или же GPU. На приведенной диаграмме (рисунок 1) для различных размеров графа (от 2^20 до 2^26) представлено время выполнения трех различных версий: последовательной, параллельной CPU и GPU. Шкала на данной диаграмме логарифмическая.
2.5 Dynamic characteristics and efficiency of the algorithm implementation
2.6 Conclusions for different classes of computer architecture
2.7 Existing implementations of the algorithm
- Boost Graph Library (функция
transitive_closure).
3 References
- ↑ Purdom, Paul, Jr. “A Transitive Closure Algorithm.” Bit 10, no. 1 (March 1970): 76–94. doi:10.1007/BF01940892.
- ↑ 2.0 2.1 Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.
- ↑ Kahn, A B. “Topological Sorting of Large Networks.” Communications of the ACM 5, no. 11 (November 1962): 558–62. doi:10.1145/368996.369025.