One step of the dqds, LAPACK

1 Links

Researched parallel implementation in C language.

2 Locality of data and computations

It is easy to see that the data locality is high. It can be further improved by placing alongside the corresponding elements of the arrays e и q. However, this does not significantly affect the algorithm performance because the ratio of the number of operations to the number of processed data is a constant.

2.1 Locality of implementation

2.1.1 Structure of memory access and a qualitative estimation of locality

Figure 1. The dqds algorithm iteration. Overall memory address profile.

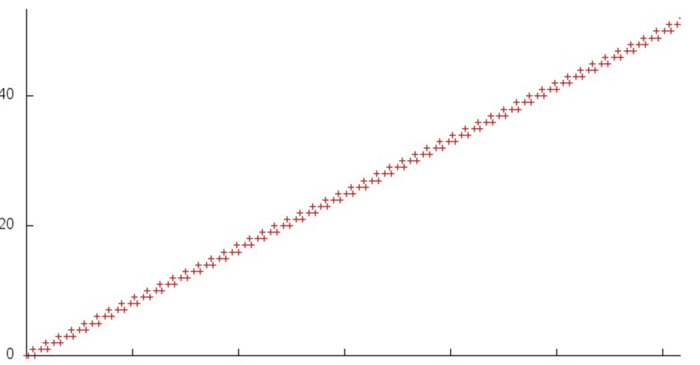
Fig.2 shows the memory address profile for one iteration of the dqds algorithm. In outward appearance, this profile has a very simple structure and consists of two serial searches performed in parallel. Notice that the overall number of memory accesses is only 3 times larger than the number of processed data. This says that the data are rarely used repeatedly, which often indicates that locality is rather poor.

Consider the structure of one search in more detail (the structure of the other search is practically the same). Fig.2 shows the small fragment 1 of Fig. 1. One can see that three memory accesses are performed at each step of the search. This indicates a high spatial locality; however, the temporal locality is low the data are used only 3 times.

Since this structure of accesses is inherent in the overall profile, the above observations are also valid for its locality.

Figure 2. The address profile, fragment 1

2.1.2 Quantitative estimation of locality

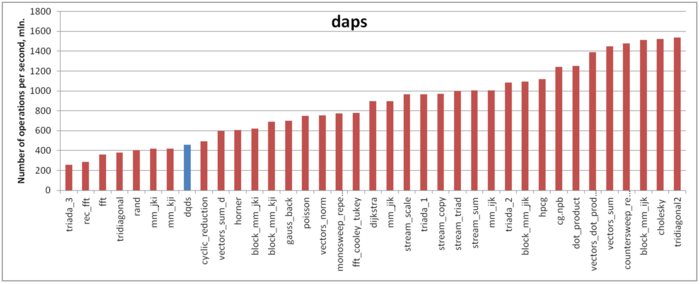
The estimate is based on daps, which assesses the number of memory access operations (reads and writes) per second. Similarly to flops, daps is used to evaluate memory access performance rather than locality. Yet, it is a good source of information, particularly for comparison with the results provided by the next estimate cvg.

Figure 3 shows the daps values for implementations of certain popular algorithms. These values are sorted in ascending order (the greater the daps, the higher the performance in general). The result is fairly unexpected, namely, the memory performance is very low. The daps estimate for this profile is comparable with those for algorithms that are most inefficient as regards memory performance such as the RandomAccess tests and inefficient variants of the conventional matrix multiplication. To some extent, this can be explained by the low temporal locality. However, here, there is another possible reason. For this implementation, the volume of computations per memory access is sufficiently large, which may cause the memory underload. In this case, performance is rather low despite the fact that the efficiency of memory interaction is on the whole not bad.

Figure 3. Comparison of daps values

3 Scalability of the algorithm and its implementations

3.1 Scalability of the algorithm

The algorithm is not scalable. The maximum acceleration is attained for two independent processors.

3.2 Scalability of of the algorithm implementation

Let us study this implementation as regards scaling out in accordance with Scalability methodology. This study was conducted using the Lomonosov-2 supercomputer of the Moscow University Supercomputing Center.

Variable parameters for the launch of the algorithm implementation and the limits of parameter variations:

• number of processors 1;
• matrix size [1000 : 260000] with the step 500.

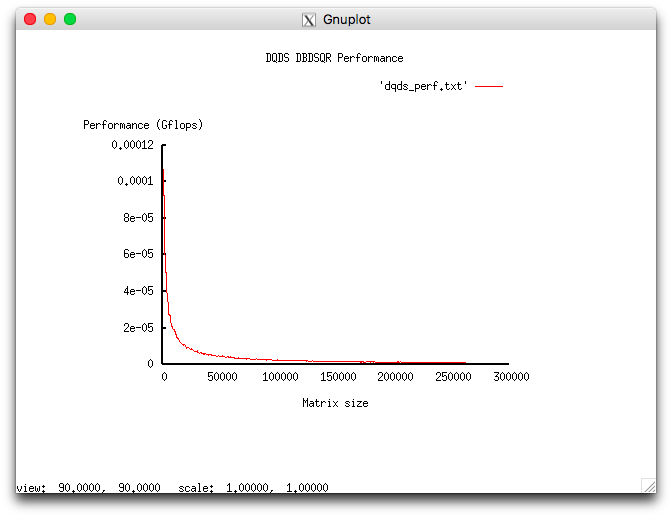
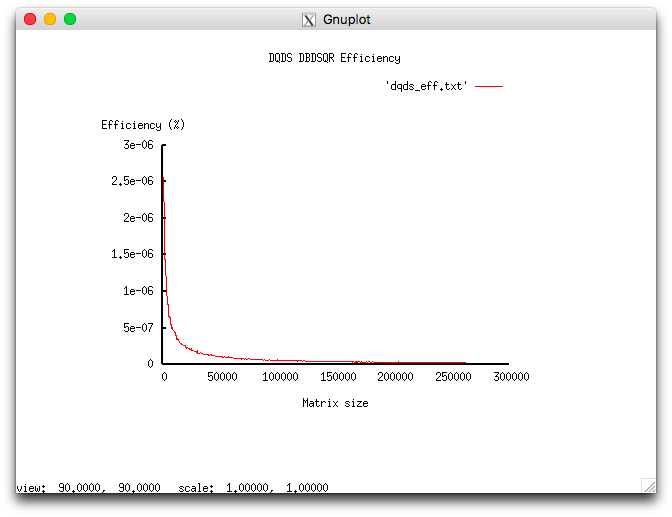
The experiments resulted in the following range of implementation efficiency:

• minimum implementation efficiency 2.559e-06%;
• maximum implementation efficiency 2.492e-08%.

The following figures show the graphs of the performance and efficiency for the chosen implementation of DQDS as functions of the variable launch parameters.

Figure 4. Parallel implementation of dqds algorithm. Performance as a function of the number of processors and the matrix size.

Figure 5. Parallel implementation of dqds algorithm. Efficiency as a function of the number of processors and the matrix size.