Givens method, locality
Primary author of this description: Vadim Voevodin (Section 2).
Contents
1 Links
The basic fragment of the implementation used for obtaining quantitative estimates is given here (функция Kernel).
2 Locality of data and computations
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
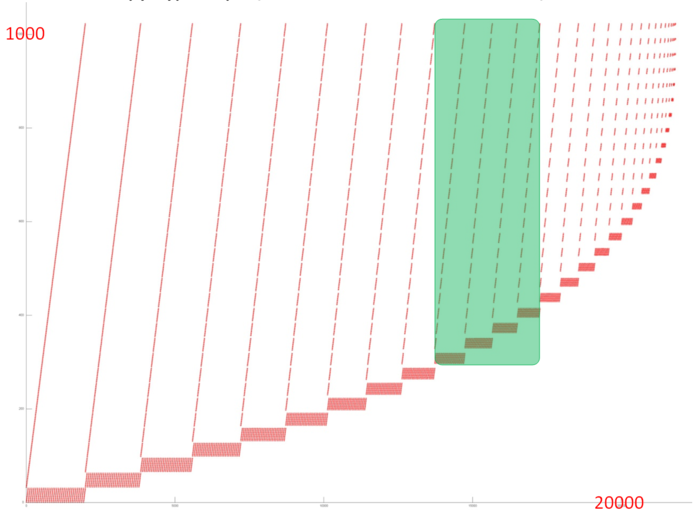
Figure 1 presents the memory access profile for an implementation of the real version of the QR decomposition of a square matrix by Givens method. This profile is formed of accesses to a single two-dimensional array storing matrix values. The profile consists of iterations of the same kind, which is clearly seen from the graph. The [math]i[/math]-th iteration affects the array entries with indices beginning from [math](i-1)*k[/math]; that is, after each iteration, the first [math]k[/math] entries are no longer processed (the value of [math]k[/math] is not known at the moment). Each iteration consists of two parts performed in parallel, namely, the successive sorting of all the entries beginning from the entry [math](i-1)*k[/math] and the active use of the first [math]i*k[/math] entries.
Judging from the general picture, one can say that the locality of this profile is fairly high. Indeed, accesses to the entries close in memory are also close in program, and there are well localized sections where the data are frequently used repeatedly. However, a more detailed analysis is needed for verifying these observations.
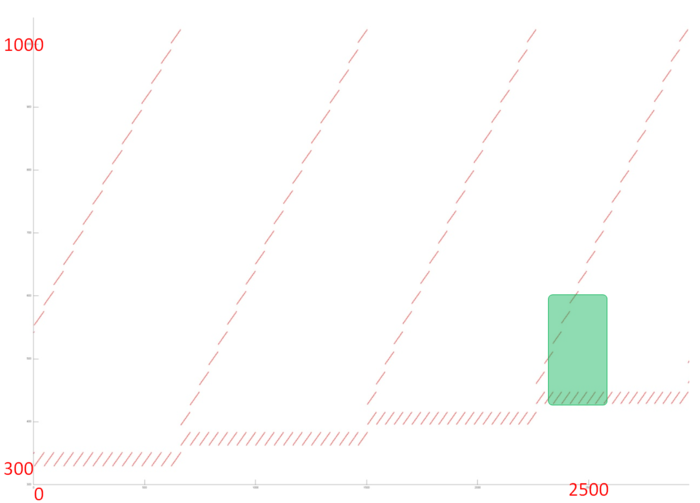
A fragment of the general profile (set out in green) is shown in fig. 2. It can be seen that, at each iteration, both parallel processes consist of small pieces resembling the conventional successive sorting. One can clearly recognize a regular structure: all the pieces have the same size and are separated by the same distance.
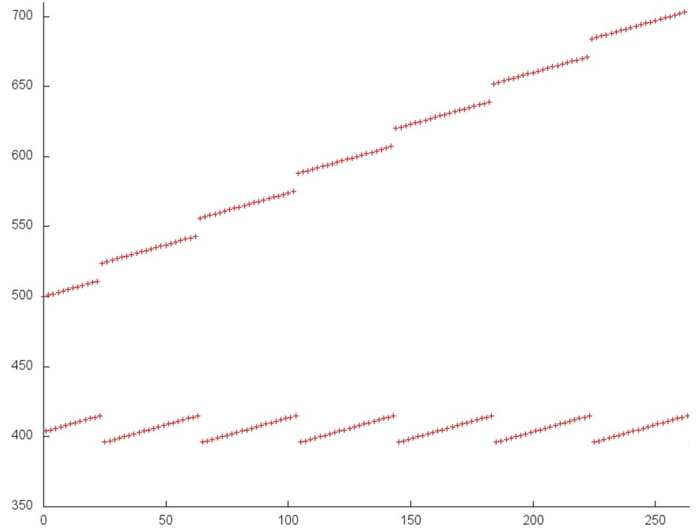
Let us look at the fragment in fig. 2 more closely. Here, individual accesses can be seen, and it is safe to say that each piece is the successive sorting of a small number of entries. At the upper part of each new piece, new entries are sorted, while, at the lower part, the same data are processed. Thus, on the whole, this fragment has a high spatial locality (both parts are successive sortings) but a medium temporal locality (because the temporal locality of the upper part is very low, while the one of the lower part is very high).
The general profile is a collection of such fragments. These fragments use the data repeatedly at different iterations; consequently, the general profile is likely of higher temporal locality. On the whole, one can say that the memory accesses in this program have a high spatial locality and a satisfactory temporal locality.